Билет 8

Наиболее полная информация о случайной величине содержится в законе её распределения. Более бедную, но зато и более конкретную информацию о ней дают её числовые характеристики. Простейшей из них является математическое ожидание, которое интерпретируется как среднее значение случайной величины. Если посмотреть на закон распределения как на распределение единичной вероятностной массы между значениями случайной величины, то в качестве среднего значения можно взять координаты центра тяжести этой массы. По известным из анализа и механики формулам получаем формулы для вычисления абсциссы центра тяжести:

xp(x)dx – в непрерывном случае, x_kp_k – в дискретном случае.

Вернёмся к изучению числовых характеристик случайных величин.

1. Выше мы ввели понятие математического ожидания для дискретной и непрерывной случайных величин.

Пусть теперь X – случайная величина с функцией распределения F(x). Возьмём произвольную функцию (x).

Назовём математическим ожиданием функции  от случайной величины X число M(X), определяемое равенством:

M(X)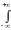 (x)dF(x).

В частности, для непрерывной случайной величины с плотностью вероятности p(x) получаем:

M(X) (x)p(x)dx,

а для дискретной случайной величины с распределением p_kP{Xx_k}:

M(X)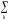 (x_k)p_k.

В случае, когда (x)x, последние три формулы принимают вид:

MX xdF(x) – в общем случае, MX xp(x)dx – в непрерывном случае, MX x_kp_k – в дискретном случае.

Формулы для непрерывного и дискретного случаев совпали с формулами для абсциссы центра тяжести распределения вероятностной массы, и тем самым оправдывается истолкование математического ожидания случайной величины X как среднего значения.

Для корректности определения математического ожидания следует обсудить вопрос о его существовании и единственности.

Вопрос о единственности M(X) возникает потому, что (X) сама является случайной величиной со своей функцией распределения F_(x) и в соответствии с нашим определением её математическое ожидание равно xdF_(x).

Для однозначности определения необходимо выполнение равенства

(x)p(x)dx xdF_(x)

и такое равенство действительно можно доказать: оно даёт правило замены переменных в интеграле Стилтьеса. Мы здесь вынуждены принять его без доказательства.

Вопрос о существовании математического ожидания: ясно, что в непрерывном и дискретном случае любая ограниченная случайная величина имеет математическое ожидание. Если же X может принимать сколь угодно большие значения, то в дискретном случае сумма, определяющая MX, становится бесконечным рядом, а в непрерывном – интеграл становится несобственным, причём оба могут расходиться. Очевидно, в непрерывном случае достаточным условием существования среднего значения у случайной величины является

p(x)O(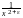 ) при x (0),

а в дискретном случае:

x_kp_kO( ) при k (0).

Однако оба эти условия не являются необходимыми.

Легко также придумать примеры случайных величин, не имеющих среднего. Для непрерывного случая таким примером может служить распределение Коши. В дискретном подобный пример придумать ещё проще, если учесть, что вероятность p_k можно приписать сколь угодно большим числам x_k.

Если дана двумерная случайная величина (X, Y), то математическое ожидание функции (X, Y) определяется равенствами

M(X, Y) (x, y)p(x, y)dxdy – в непрерывном случае (интеграл берётся по всей плоскости),

M(X, Y) (x_i, y_j)p_ij – в дискретном случае (сумма берётся по всем возможным значениям двумерной случайной величины).

2. Второй по важности числовой характеристикой случайной величины X служит её дисперсия DX. Дисперсией называется

DXM[(XMX)²] (xMX)²dF(x),

т. е. среднее значение квадрата отклонения случайной величины от её среднего. Эта формула в непрерывном случае переходит в

DX (xMX)²p(x)dx,

а в дискретном в:

DX (x_kMX)²p_k.

Если среднее есть не у всех случайных величин, то дисперсия и подавно. В дальнейшем все теоремы о MX и DX без особых оговорок формулируются лишь для тех X, которые их имеют.

Размерность дисперсии равна квадрату размерности случайной величины X. Поэтому иногда удобно вместо DX рассматривать величину _X , называемую средним квадратичным отклонением случайной величины X или просто стандартом.

Дисперсия и стандарт мыслятся как меры разброса значений случайной величины вокруг её среднего.