Формула полной вероятности.

Рассмотрим систему A из k попарно несовместных событий.

B₁, B₂, ..., B_k

Пусть дано событие A, удовлетворяющее равенству A=B₁A+B₂A+...+B_kA.

Показать, что события B₁A, B₂A, B_kA попарно несовместны. B_iAB_jA=B_iB_jAA=VAA=V

Найти вероятность наступления события A. Любое событие входящее в A, обязательно входит в некоторое, но одно B_i, т.к. B₁, B₂, ..., B_k образуют полную группу.

Т.к. B₁, B₂, ..., B_k несовместны, то по третей аксиоме теории вероятности имеем:

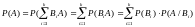; т.е.

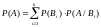
Билет 4

Часто интерес представляет случай большого числа n и малой вероятности p успеха в одном отдельном испытании. В этом случае удобно воспользоваться приближением Пуассона.

Теорема: Если вероятность p наступления события А в каждом испытании постоянна, близка к нулю, а число независимых испытаний n достаточно велико, то вероятность Pn(k) того, что в n независимых испытаниях событие А наступит k раз, приближенно равна:

, где λ=np

Эта формула называется формулой Пуассона. Обычно приближенную формулу Пуассона применяют, когда p<0,1, а npq<10.

Функция затабулирована, т.е. имеет таблицу.

Билет 5

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

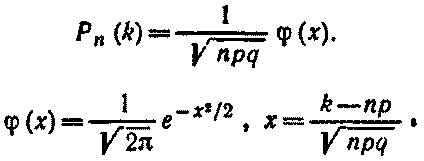
Для определения значений φ(x) можно воспользоваться специальной таблицей.

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна

P(k1;k2)=Φ(x'') - Φ(x')

Здесь

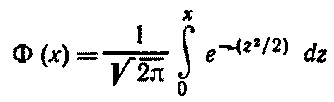-функция Лапласа

Значения функции Лапласа находят по специальной таблице.

Билет 6

Пусть имеется вероятностное пространство вида .

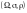Случайной величиной называется измеримая числовая скалярная функция , элементами которой являются элементарные события.

Числовая скалярная функция - это функция, удовлетворяющая следующему условию:

событие - алгебре и, следовательно, имеет вероятность наступления.

Если произведено испытание, в результате которого произошло некоторое элементарное событие . В соответствии с функцией этому элементарному событию соответствует число, которое называется реализацией случайной величины x в данном испытании.

В соответствии с определением случайной величины вводится числовая скалярная функция F(x), 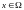, определенная для каждого действительного x и по определению равная вероятности наступления события:

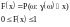
Эта функция называется функцией распределения случайной величины .

Рассмотрим три события:

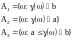
где a<b, a, b - действительные числа.

Свойства:

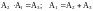
Покажем, что из факта

A₂-алгебре

A₁ алгебре

и равенства 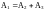следует, что A₃

По определению -алгебры A₃ измерима, поэтому можно принять III аксиому теории вероятности:

F(x) - неубывающая функция

Если x<y, то

т.к. , то преобразования верны.

Определение1: Случайная величина называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Задание дискретной случайной величины по определению равносильно заданию закона распределения случайной величины в следующем виде:

где

Следующее утверждение отражает связь между функцией распределения дискретной случайной величины и законом распределения случайной величины.

Утверждение 1: Закон распределения и функция распределения дискретной случайной величины взаимно однозначно определяют друг друга.

Непрерывные случайные величины

Определение 2: Распределение случайной величины называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого ,

где - интегрируемая по Лебегу функция. Функция называется плотностью распределения случайной величины .

Теорема 1: Для того чтобы случайная величина была непрерывной случайной величиной, необходимо и достаточно, чтобы для любого

(1)

Замечание 1: Из представления (1) видно, что функция распределения непрерывной случайной величины является непрерывной функцией.

Свойства плотности распределения:

1)

2) почти всюду.

3) для любых х, являющихся точками непрерывности плотности.

Теорема 2: Для того, чтобы функция p = p(x) была плотностью распределения некоторой случайной величины , необходимо и достаточно, чтобы она удовлетворяла свойствам 1) и 2) плотности.