
- •Содержание:
- •Расчёт валов на прочность и жёсткость.
- •Расчёт на прочность балок при плоском поперечном изгибе.
- •Определение перемещений при плоском изгибе. Расчёт на жёсткость.
- •Сложное сопротивление.
- •Косой изгиб.
- •Вне центренное растяжение и сжатие.
- •Определение положения нулевой линии.
- •Ядро сечения.
- •Построение ядра сечения для простейших фигур.
- •Устойчивость сжатых стержней.
- •Формула Эйлера для определения .
- •Учёт влияния способов закрепления стержня на критическую силу.
- •Критические напряжения. Гибкость стержня.
- •Приделы применимости формулы Эйлера.
- •Формула Ясинского.
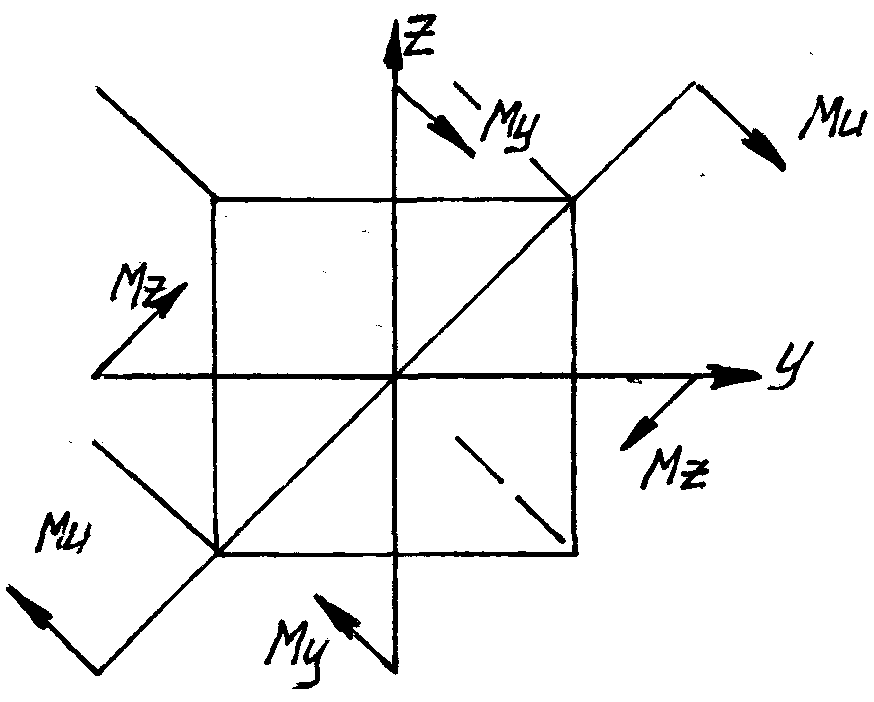
Косой изгиб.
Косым изгибом называют деформацию, при котором полный изгибающий момент не совпадает ни с одной из главных осей инерции.
Однако мы будем учитывать только действие изгибающих моментов.
![]()
![]()
Для определения напряжений при косом изгибе:
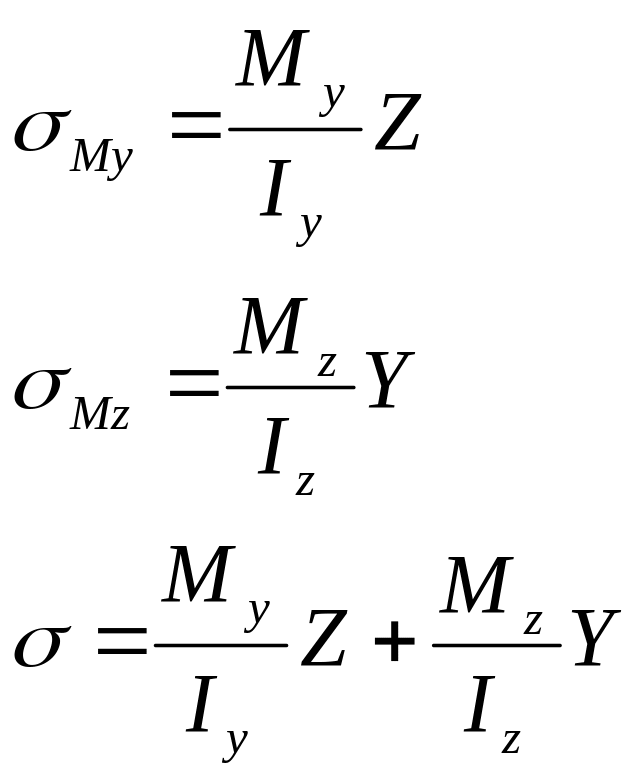
![]() моменты
инерции.
моменты
инерции.
![]() главные
центральные оси.
главные
центральные оси.
Основная задача заключается в том, чтобы определить опасные точки, т.е. точки, где напряжение максимально по модулю. Любой изгиб, плоский или косой, сопровождается с одной стороны растяжением, а с другой сжатием. А слой, длина которого не изменяется, этот слой называется нейтральным.
В плоскости поперечных сечений нейтральный слой оставляет прямую нулевую линию.
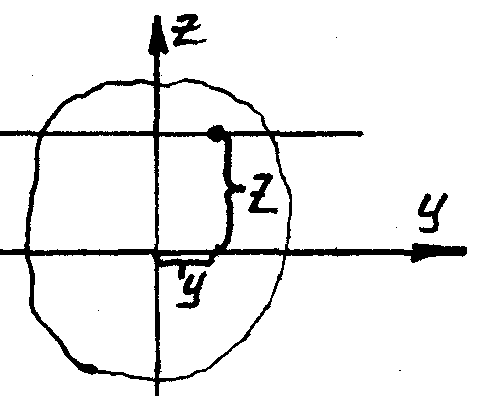
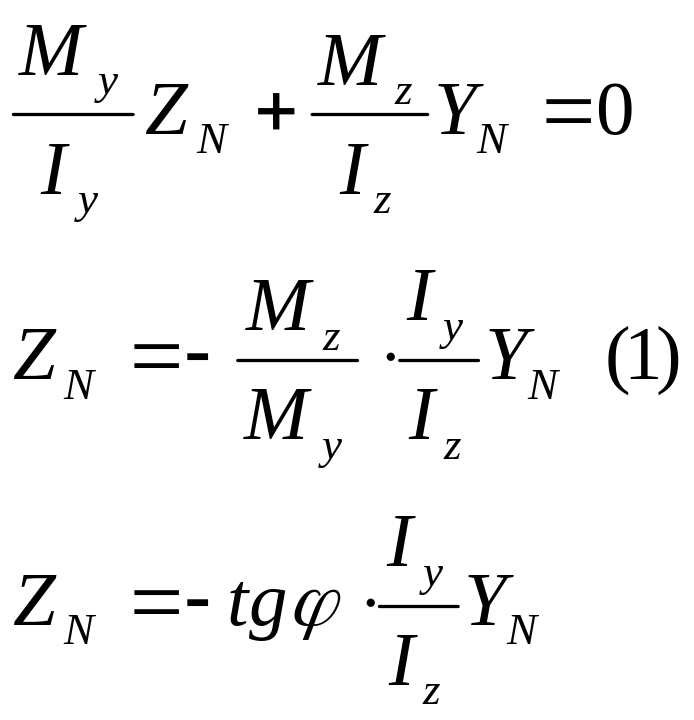
Уравнение нулевой линии – это будет прямая.
![]()
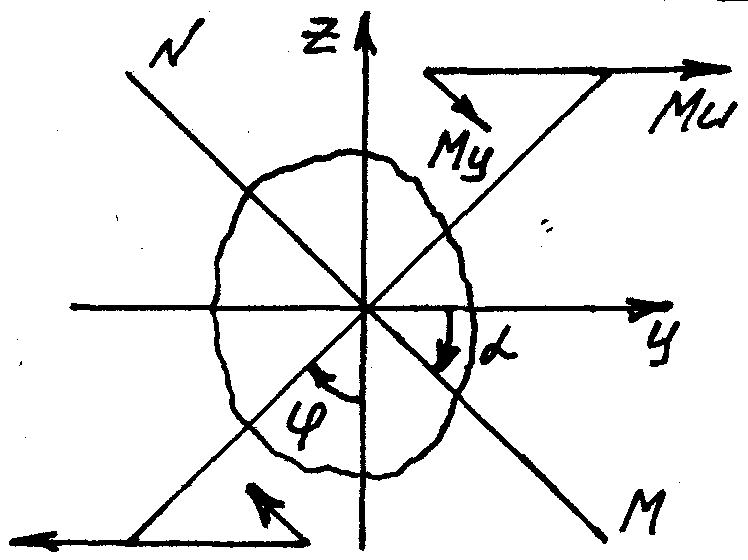 будем
считать положительным, если значения
будут отсчитываться от оси Z к полному
изгибающему моменту
по часовой стрелке.
будем
считать положительным, если значения
будут отсчитываться от оси Z к полному
изгибающему моменту
по часовой стрелке.
![]()
![]() будет
положительным, если он будет отсчитываться
от оси Y.
будет
положительным, если он будет отсчитываться
от оси Y.
Расчёт на прочность при косом изгибе.
![]()
Экстремальные
значения
![]() ,
нормальных напряжений, будут достигаться
в наиболее удалённых от нулевой линии
точках.
,
нормальных напряжений, будут достигаться
в наиболее удалённых от нулевой линии
точках.
Порядок расчёта на прочность.
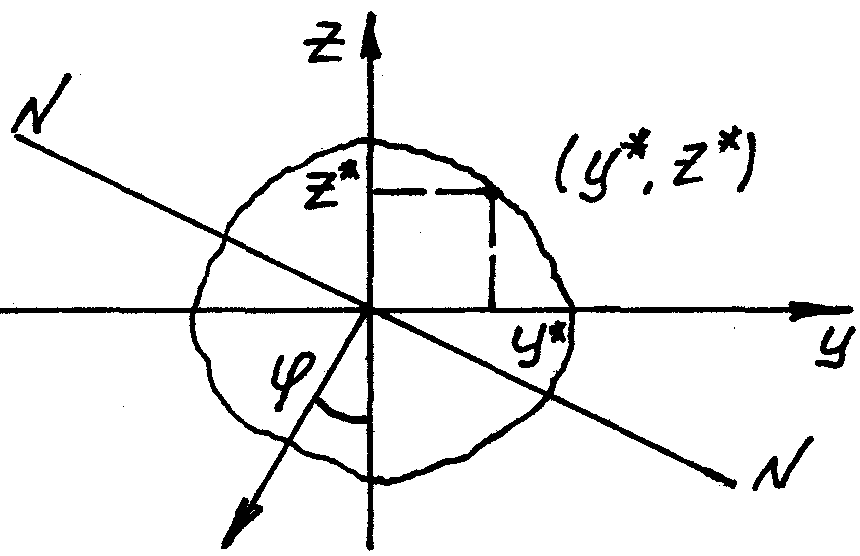 Мы
определяем положение нулевой линии по
формуле (1) или (2).
Мы
определяем положение нулевой линии по
формуле (1) или (2).Определяем координаты точек наиболее удалённых от нулевой линии.
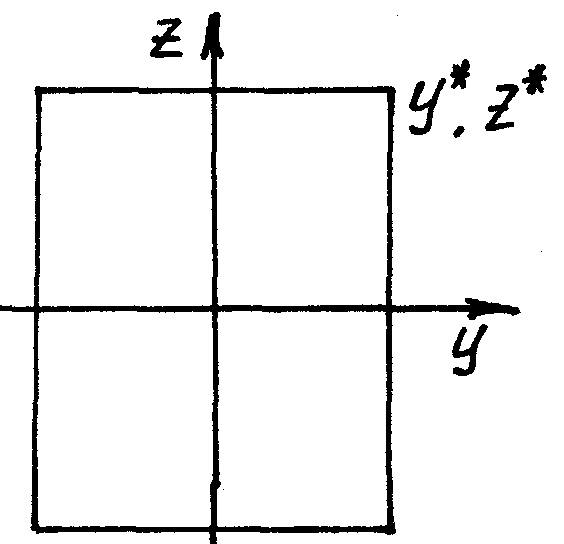
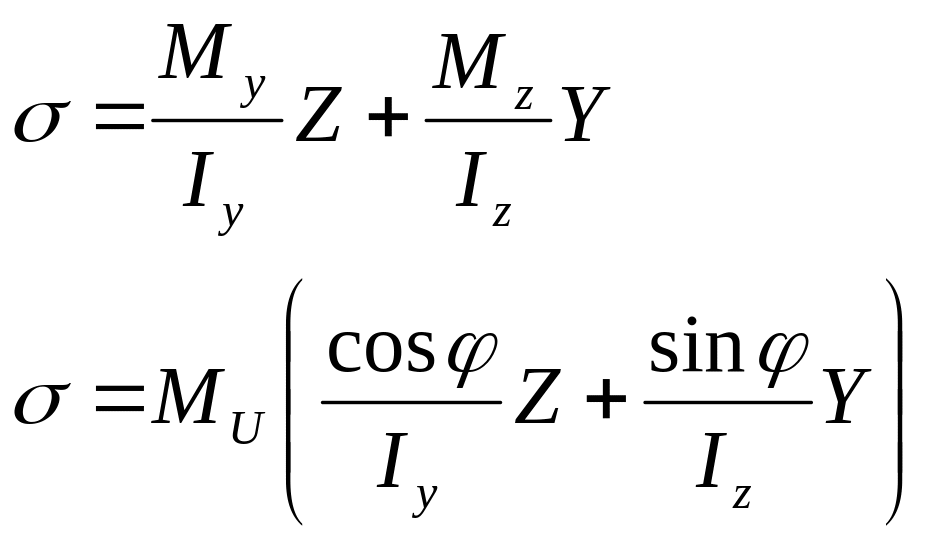
Если
![]() ,
то уравнение прочности записывается
следующим образом:
,
то уравнение прочности записывается
следующим образом:

Это справедливо только для прямоугольника и двутавра.
Определение прогибов и расчёт на жёсткость при косом изгибе.

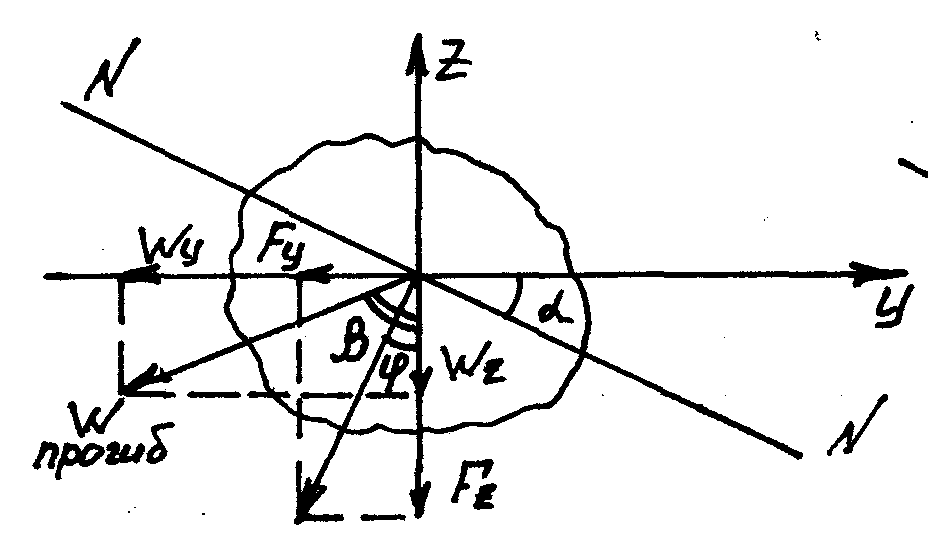
![]() определяем
как при косом изгибе.
определяем
как при косом изгибе.
![]()
Направление прогиба и направление нулевой линии взаимно перпендикулярно.
![]()
Изгиб с кручением грузьев круглого поперечного сечения.
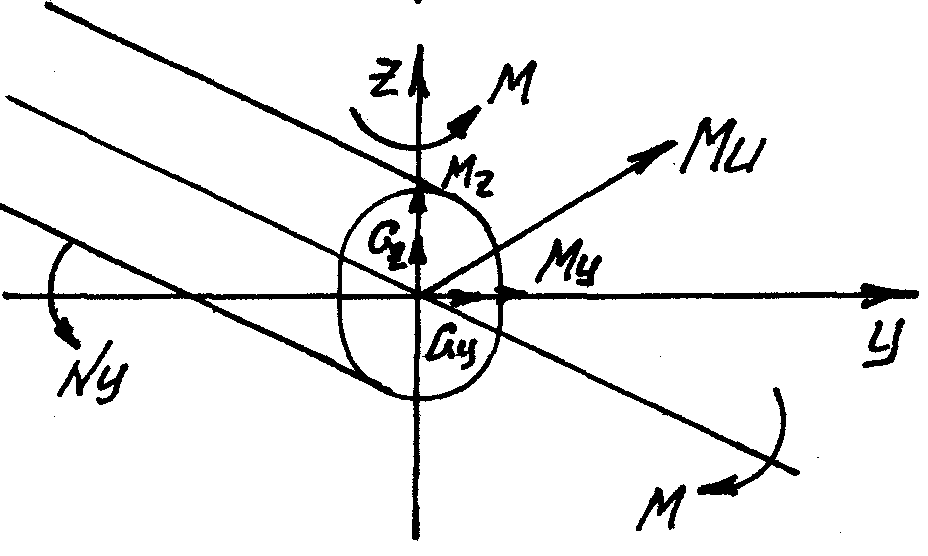 Изгиб
с кручением называется такой тип
деформации, при котором в поперечных
сечениях стержня действует одновременно
и изгибающий и крутящий момент.
Изгиб
с кручением называется такой тип
деформации, при котором в поперечных
сечениях стержня действует одновременно
и изгибающий и крутящий момент.
![]()
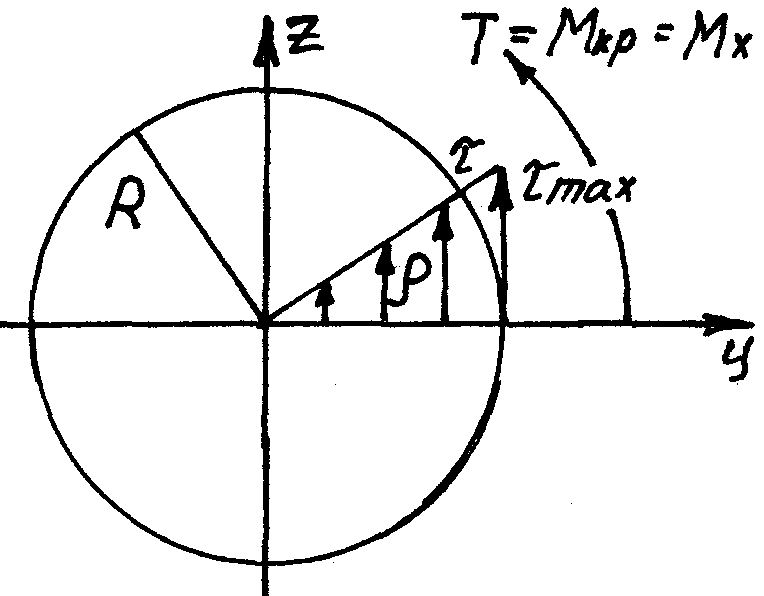 Мы
будем рассматривать брусья, в сечении
которых круг или кольцо.
Мы
будем рассматривать брусья, в сечении
которых круг или кольцо.
Здесь наблюдается косой изгиб. Наша задача установить опасные точки сечения.
![]()
При действии крутящего момента в сечении возникают касательные напряжения, которые будут максимальными.
![]() пренебрегаем
(т.к. они малы), то касательные напряжения
не будем считать, изгибающие моменты
пренебрегаем
(т.к. они малы), то касательные напряжения
не будем считать, изгибающие моменты
![]() будут создавать нормальные напряжения.
будут создавать нормальные напряжения.
![]()
Полный
изгибающий момент:
![]() .
.
Таким образом будут действовать:
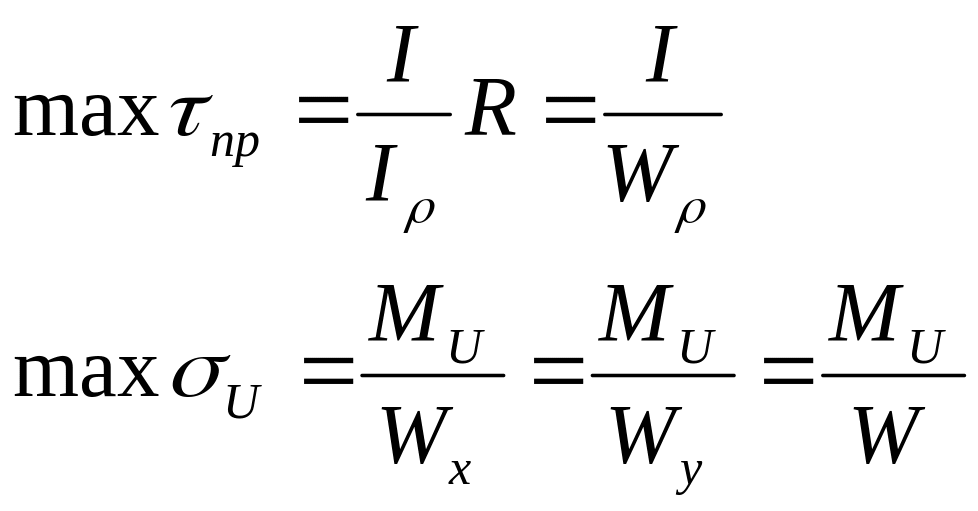
![]() полярный
момент сопротивления
полярный
момент сопротивления
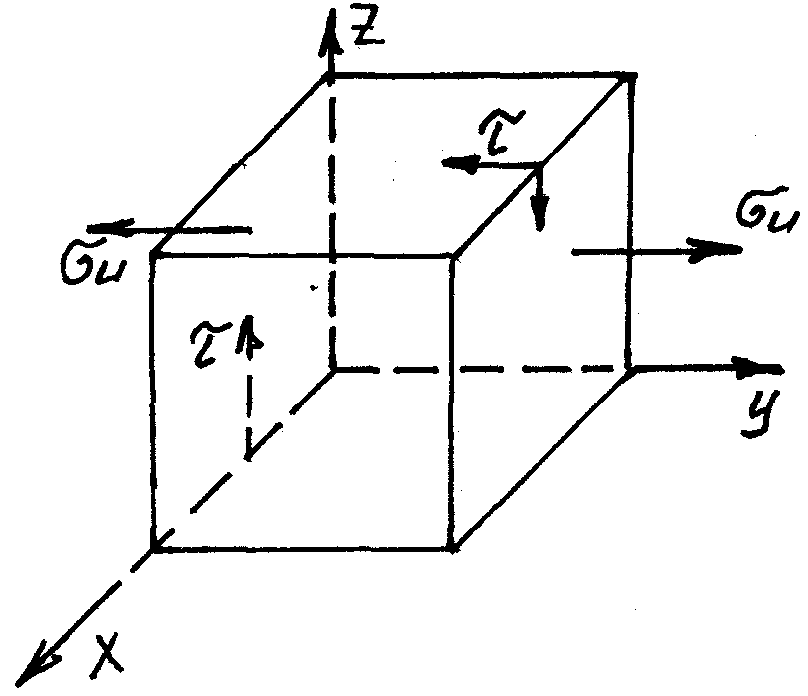
![]() осевые
моменты.
осевые
моменты.
Для
круга и кольца:
![]()
Рассмотрим элемент в окрестности опасных точек, будет иметь плоское наряжённое состояние.
При расчёте мы будем пользоваться одной теорией прочности.
Мы будем пользоваться 3 и 4 теорией прочности.
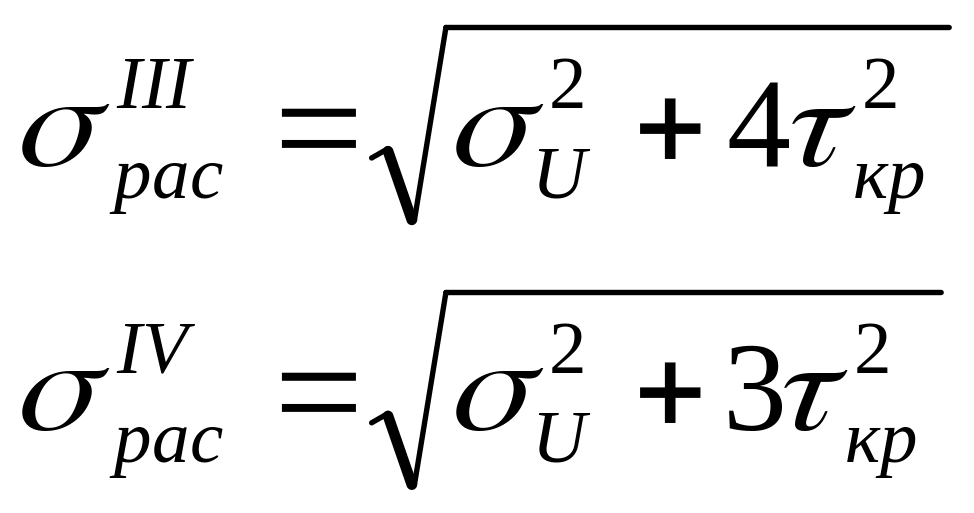
В окрестности опасных точек плоское напряжённое состояние. Мы рассматривали произвольные точки.

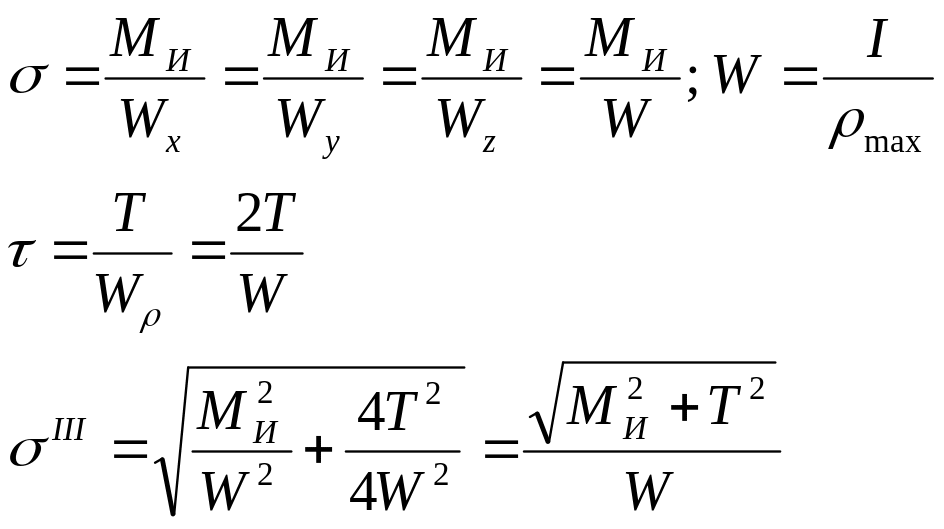
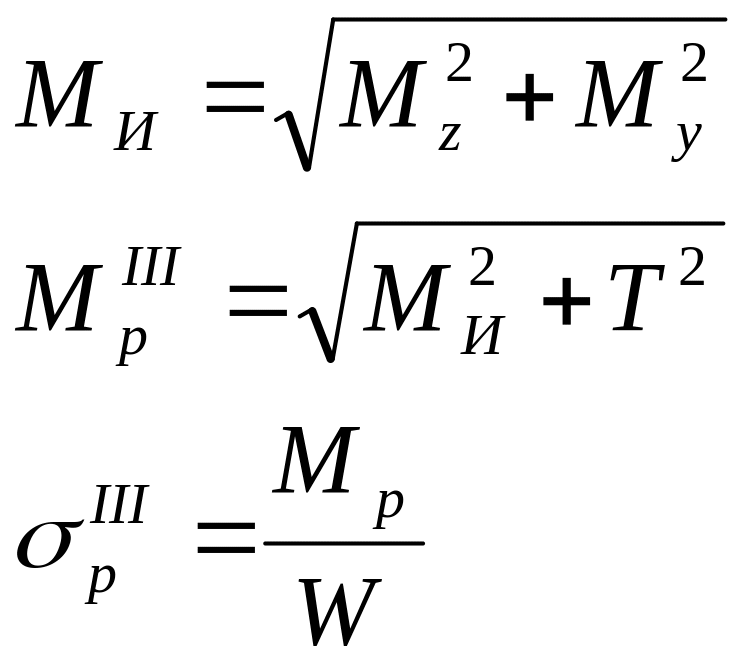


Произвести расчёты.
![]()
Опасное сечение заделки.
Строим эпюру для крутящих моментов .
Определяем опасные сечения.
Проводим расчёт сечений.
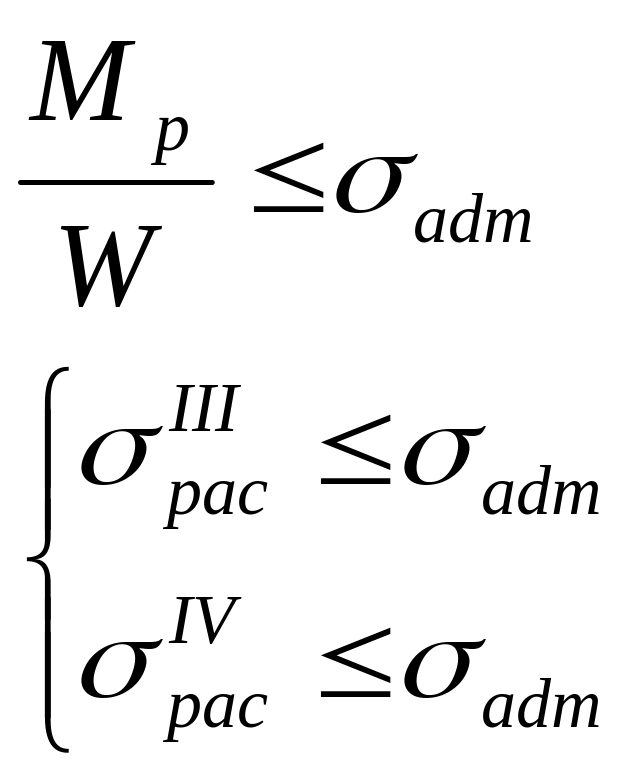
Вне центренное растяжение и сжатие.
Если внешние и продольные силы действуют параллельно оси стрежня но не совпадает с этой осью, то такой вид деформации называется вне центренным растяжением, сжатием.

Вне
центренное растяжение и сжатие
характеризуется продольной силой N и
![]() .
.
![]()
![]() точка
приложения силы – полюс.
точка
приложения силы – полюс.
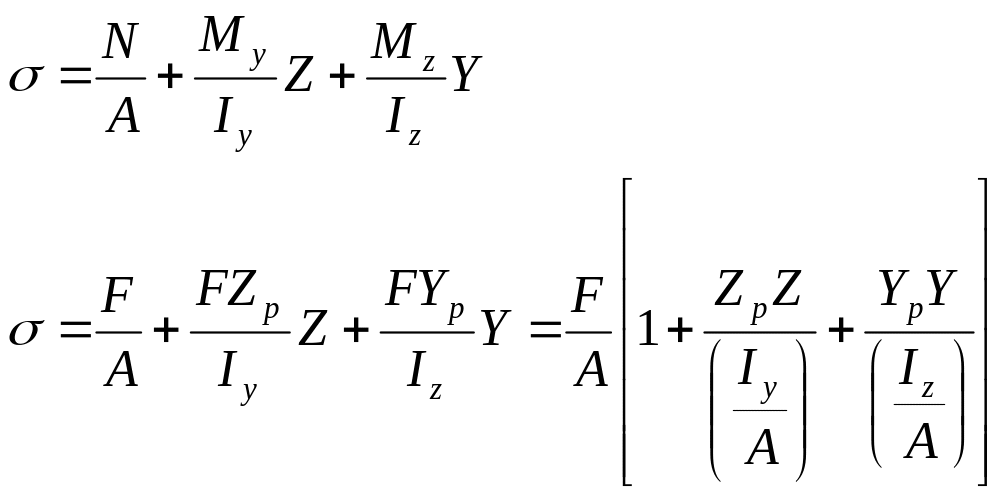
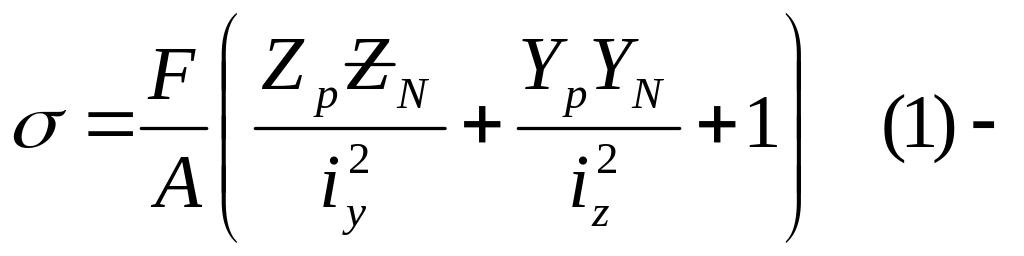 формула
для определения вне центренного
растяжения, сжатия.
формула
для определения вне центренного
растяжения, сжатия.
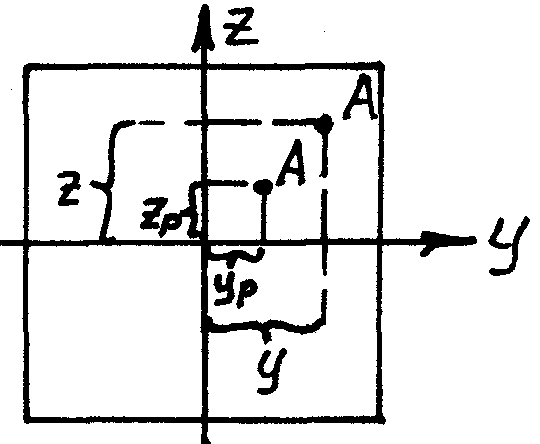
![]()
![]() радиус
инерции сечения.
радиус
инерции сечения.
Формула определяет с точностью до знака, в зависимости от выбора осей и направления действия силы.
