
- •Содержание:
- •Расчёт валов на прочность и жёсткость.
- •Расчёт на прочность балок при плоском поперечном изгибе.
- •Определение перемещений при плоском изгибе. Расчёт на жёсткость.
- •Сложное сопротивление.
- •Косой изгиб.
- •Вне центренное растяжение и сжатие.
- •Определение положения нулевой линии.
- •Ядро сечения.
- •Построение ядра сечения для простейших фигур.
- •Устойчивость сжатых стержней.
- •Формула Эйлера для определения .
- •Учёт влияния способов закрепления стержня на критическую силу.
- •Критические напряжения. Гибкость стержня.
- •Приделы применимости формулы Эйлера.
- •Формула Ясинского.
Содержание:
Стр.
Расчёт валов на прочность и жёсткость. 3
Расчёт на прочность балок при плоском поперечном изгибе. 4
Определение перемещений при плоском изгибе. Расчёт на жёсткость. 6
Сложное сопротивление. 7
Косой изгиб. 8
Расчёт на прочность при косом изгибе. 9
Порядок расчёта на прочность. 9
Определение прогибов и расчёт на жёсткость при косом изгибе. 9
Изгиб с кручением грузьев круглого поперечного сечения. 9
Вне центренное растяжение и сжатие. 11
Определение положения нулевой линии. 11
Ядро сечения. 12
Построение ядра сечения для простейших фигур. 12
Устойчивость сжатых стержней. 13
Формула Эйлера для определения . 14
Учёт влияния способов закрепления стержня на критическую силу. 15
Критические напряжения. Гибкость стержня. 15
Приделы применимости формулы Эйлера. 15
Формула Ясинского. 15
Расчёт валов на прочность и жёсткость.
Вал
– это прямолинейный стержень, обычно
круглого или кольцеобразного сечения,
который испытывает действие крутящего
момента. В поперечных сечениях вала
действует только внутренний и крутящий
момент (![]() или
или
![]() ).
).
![]()
Задача
заключается в том, чтобы по известным
крутящим моментам и геометрии, определить
напряжение. Затем определяется
максимальное напряжение (![]() ):
):![]() .
.
З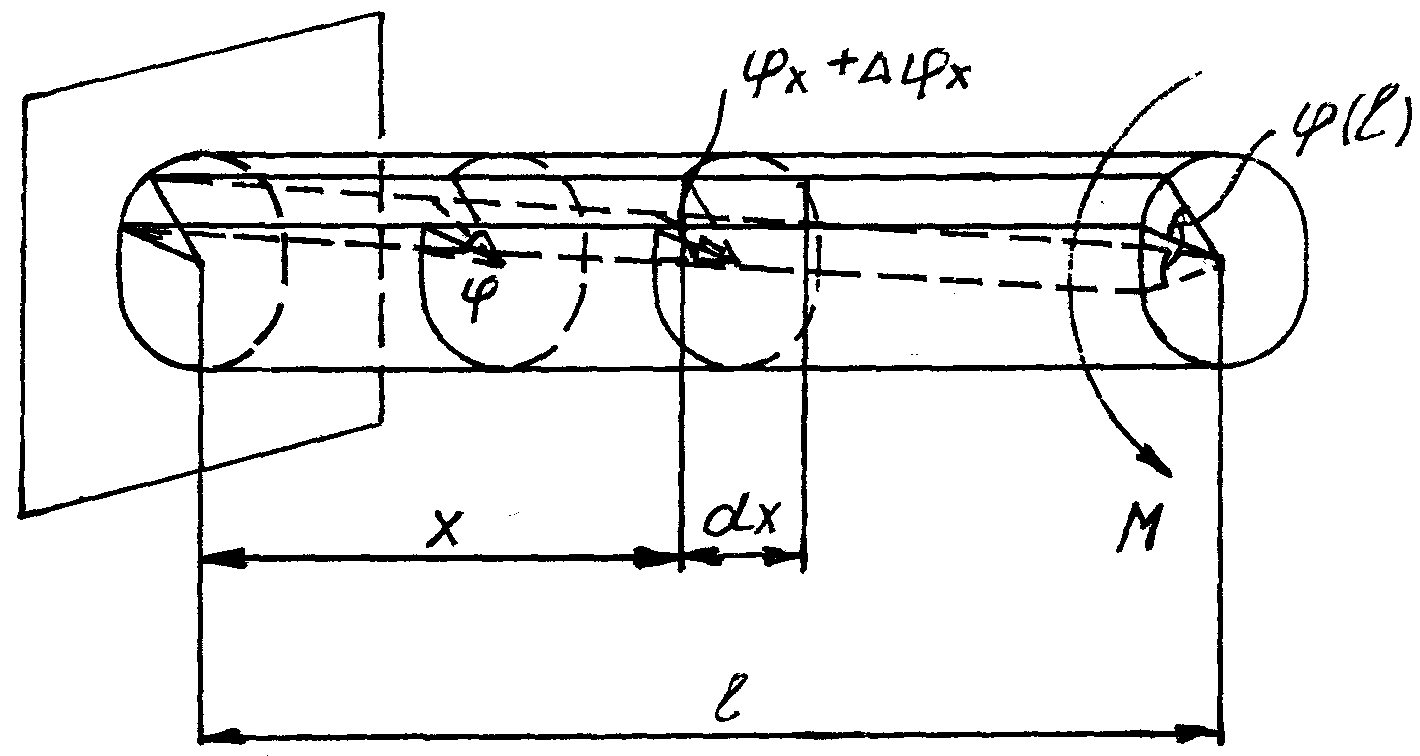 адача
определения касательных напряжений
осуществляется с помощью следующих
гипотез:
адача
определения касательных напряжений
осуществляется с помощью следующих
гипотез:
Сечения плоские до напряжения остаются плоскими, и после напряжения. Они лишь поворачиваются на некоторый угол
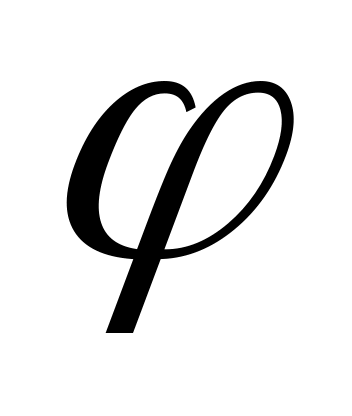 относительно друг друга.
относительно друг друга.
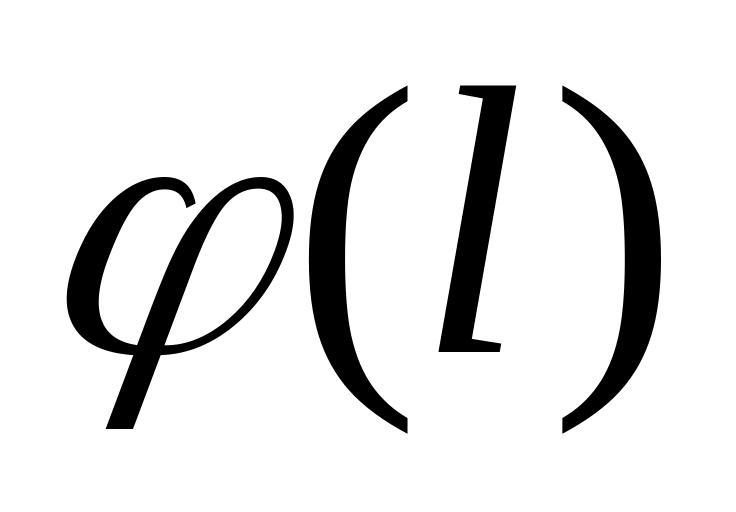 – полный угол поворота в сечении после
нагружения вала.
– полный угол поворота в сечении после
нагружения вала.
![]() – относительный
угол поворота (относительный угол
закручивания).
– относительный
угол поворота (относительный угол
закручивания).
![]() – они характеризуют степень деформации
и по этим параметрам производят расчёт
на жёсткость.
– они характеризуют степень деформации
и по этим параметрам производят расчёт
на жёсткость.
Расстояние между сечениями не изменяются. Следовательно, в точках поперечного сечения нормальное напряжение отсутствует.
Радиусы поперечных сечений не изменяются и не меняют свои углы. Касательные напряжения должны быть перпендикулярны в каждой точке сечения. Поскольку радиусы не исправляются, закон изменения касательных напряжений является линейным.
На основании гипотез 1, 3 можно сделать вывод, что касательные напряжения перпендикулярны к радиусу и зависят от положения точки.
![]()
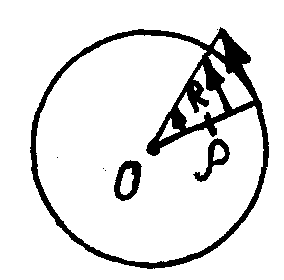
– крутящий момент сечения
![]() –
расстояние
от центра до точки
–
расстояние
от центра до точки
![]() –
полярный
момент инерции
–
полярный
момент инерции
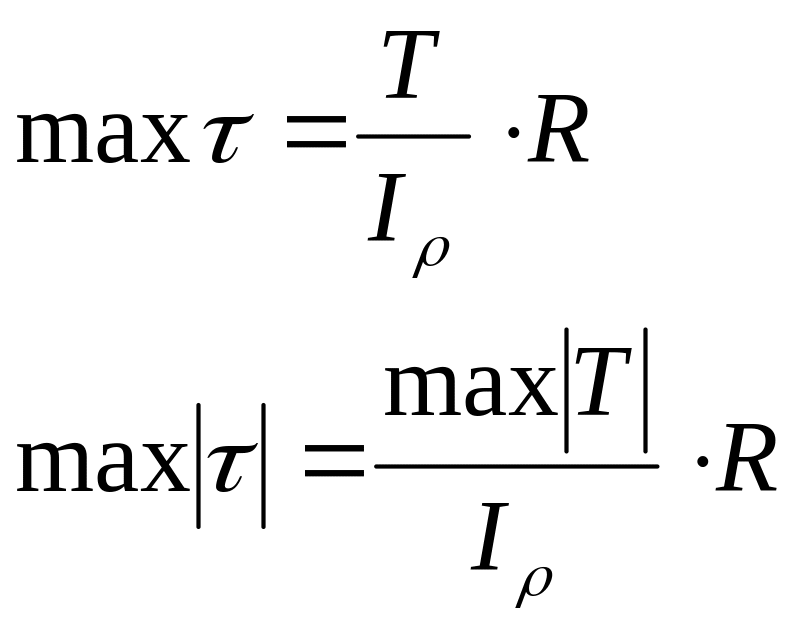
![]() –
теория
прочности
–
теория
прочности
![]()
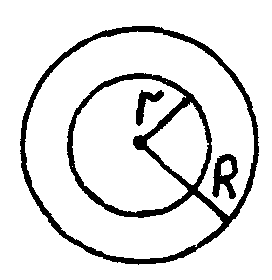 –
для
круга
–
для
круга
![]()
Для расчёта на жёсткость необходимо вычислить углы поворота относительно поперечных сечений.
![]()
![]() –
модуль
сдвига или модуль упругости второго
рода.
–
модуль
сдвига или модуль упругости второго
рода.
Если
![]() ,
где
,
где
![]() ,
то
,
то
![]()
![]()
![]() –
условия
прочности
–
условия
прочности
![]() –
условия
жёсткости
–
условия
жёсткости
Расчёт на прочность балок при плоском поперечном изгибе.
Рассмотрим прямолинейный груз постоянного поперечного сечения. Плоскости которые содержат продольную ось прямолинейного стержня и одну из главных осей поперечного сечения, называются главными плоскостями.
![]()
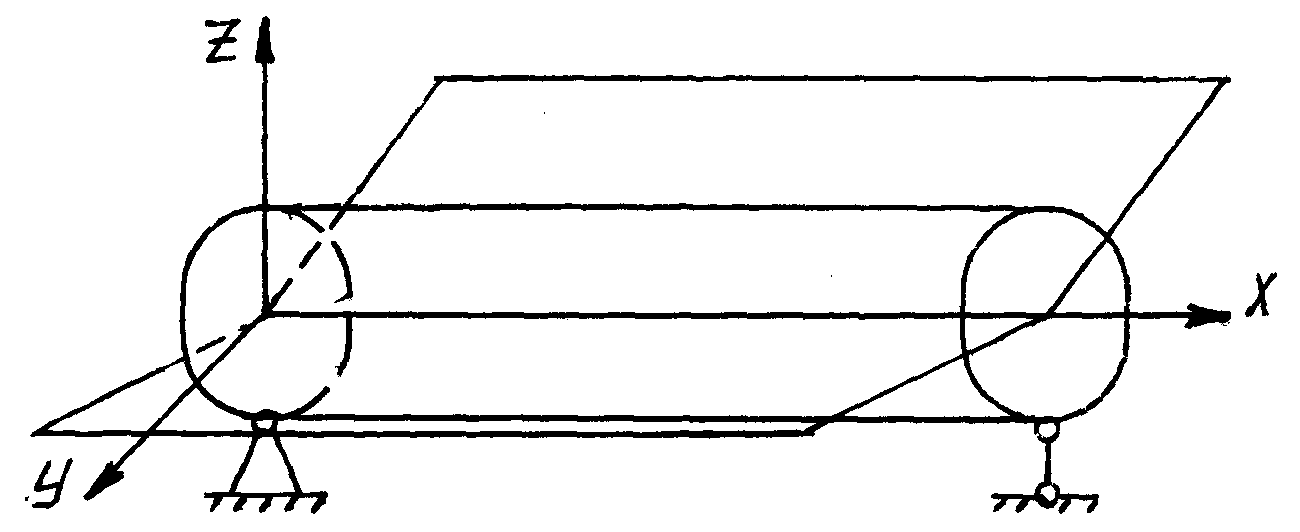

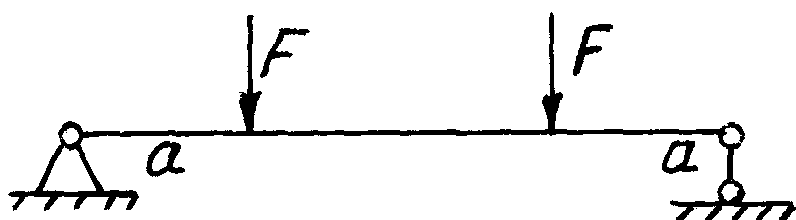 –
главные
оси.
–
главные
оси.
![]() –
главные плоскости. Эти плоскости взаимно
перпендикулярны. Если внешние нагрузки
лежат в одной из главных плоскостей и
перпендикулярно продольной оси, то
такой вид деформации называется плоским
изгибом.
Если в поперечных сечениях только
изгибающий момент не равен нулю, то
такой вид деформации называется чистым
изгибом.
А если и изгибающий момент, и поперечная
сила не равны нулю, то изгиб называется
поперечным.
–
главные плоскости. Эти плоскости взаимно
перпендикулярны. Если внешние нагрузки
лежат в одной из главных плоскостей и
перпендикулярно продольной оси, то
такой вид деформации называется плоским
изгибом.
Если в поперечных сечениях только
изгибающий момент не равен нулю, то
такой вид деформации называется чистым
изгибом.
А если и изгибающий момент, и поперечная
сила не равны нулю, то изгиб называется
поперечным.
Предположим,
что внешние нагрузки действуют в
плоскости
![]() ,
которая приводит к поперечному изгибу,
т.е. в поперечном сечении действует
,
которая приводит к поперечному изгибу,
т.е. в поперечном сечении действует
![]() и
и
![]() .
Задача заключается в том чтобы зная
величины внутренних напряжений,
определить нормальные и касательные
напряжения. Предположим, что справедлив
принцип независимости действия сил,
т.е. результат действия
.
Задача заключается в том чтобы зная
величины внутренних напряжений,
определить нормальные и касательные
напряжения. Предположим, что справедлив
принцип независимости действия сил,
т.е. результат действия
![]() не зависит от действия
.
При определении нормальных напряжений
применяем следующий гипотезы:
не зависит от действия
.
При определении нормальных напряжений
применяем следующий гипотезы:
Поперечные сечения плоские и параллельные до деформации, остаются и после деформации (гипотеза Бернулли).
Размеры и форма поперечного сечения не изменяется. Продольные слои испытывают одинаковые деформации по ширине слоя. Продольные слои не давят друг на друга. По высоте сечения нормальные напряжения изменяются пропорционально.
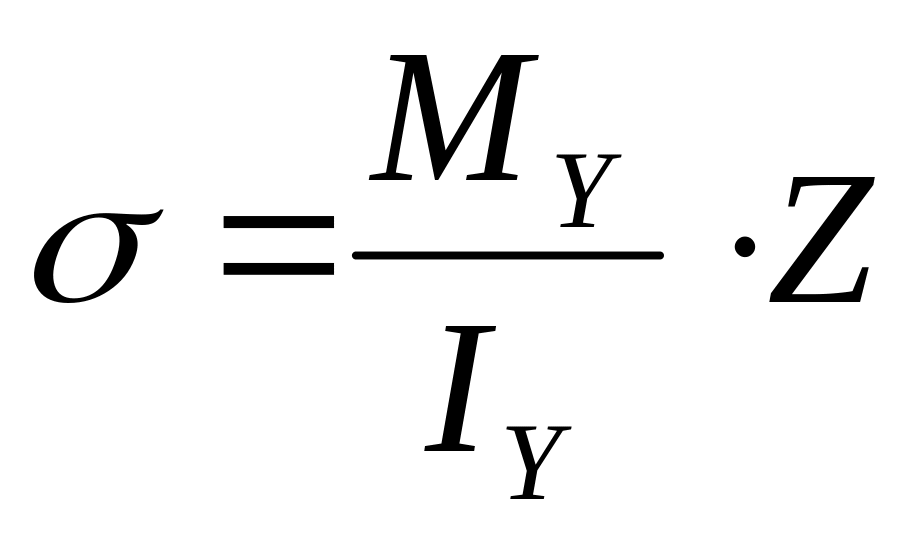
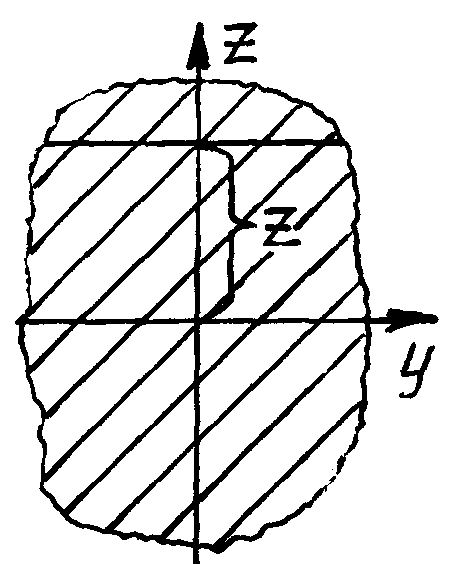 (
( –
координата)
–
координата)
–
главные
центральные оси. Линия, где
![]() ,
называется нулевой
линией и
будет совпадать с главными центральными
осями. Нулевая линия делит на две части:
на область растяжения и сжатия. Для
определения касательных напряжений
используется следующая гипотеза:
,
называется нулевой
линией и
будет совпадать с главными центральными
осями. Нулевая линия делит на две части:
на область растяжения и сжатия. Для
определения касательных напряжений
используется следующая гипотеза:
![]() .
В каждой точке сечения направления
касательных напряжений совпадает с
касательными напряжениями.
.
В каждой точке сечения направления
касательных напряжений совпадает с
касательными напряжениями.
По ширине сечения касательные напряжения не изменяются.
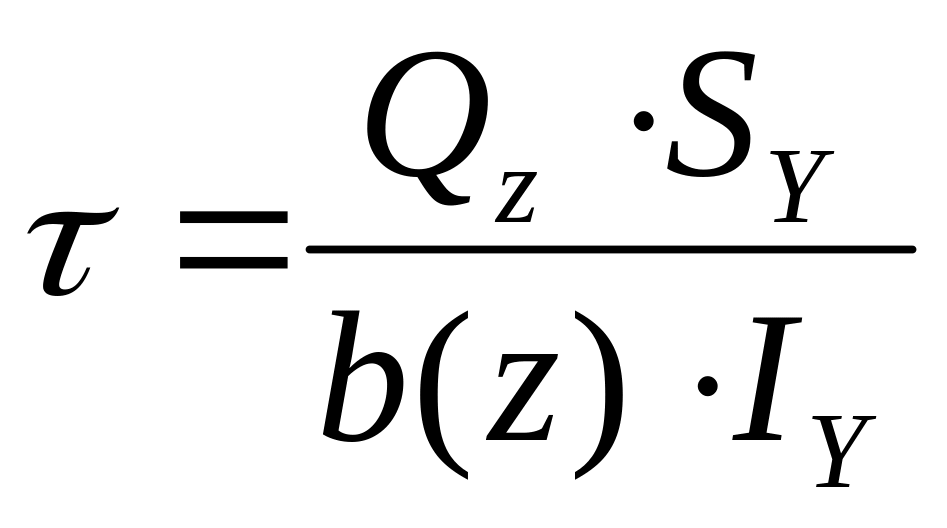 –
формула Журавского.
–
формула Журавского.
– главные центральные оси.
Главные центральные оси совпадают с нулевой линией.
Н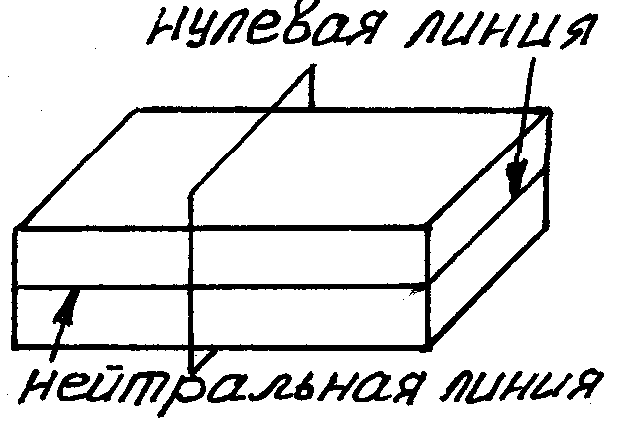 улевая
линия – это
линия, относительно которой нормальное
напряжение рано нулю. Нулевая линия
получается в результате пересечения
нейтральной оси с плоскостью поперечного
сечения.
улевая
линия – это
линия, относительно которой нормальное
напряжение рано нулю. Нулевая линия
получается в результате пересечения
нейтральной оси с плоскостью поперечного
сечения.
Нейтральный слой – длина волокон.
Нулевая делит на две области: область растяжения и сжатия.
![]() –ширина
отсечённой части на уровне Z
–ширина
отсечённой части на уровне Z
![]() –статический
момент отсечённой части
–статический
момент отсечённой части
![]() –момент
инерции относительно главной центральной
оси
–момент
инерции относительно главной центральной
оси
![]() –поперечная
сила сечения
–поперечная
сила сечения
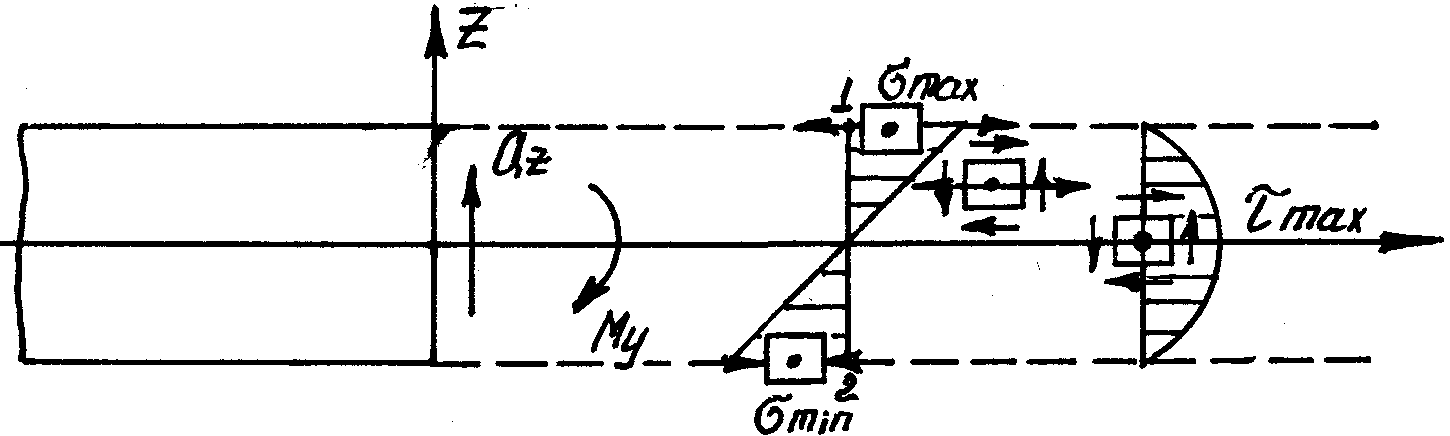
Как
обеспечить прочность нашей балки при
плоском изгибе? Чтобы обеспечить
прочность балки от разрушения в точках
1 и 2, необходимо выполнить условие:
![]() .
.
В точках вида 3 имеет место напряжённое состояние чистого сгиба, и чтобы обеспечить балку от разрушения необходимо чтобы выполнялось условие: .
В точках типа 4 – имеет место плоское напряжённое состояние, т.е. в двух площадках действует нормальное и касательное напряжение и как правило для обеспечения прочности балки используют третью или четвёртую теорию прочности.
![]()
