Электродвижущая сила катушки

Вращающееся магнитное поле, сцепляясь с катушками обмотки статора, наводит в них ЭДС. Мгновенное значение ЭДС (В) одной катушки с числом витков w_k,

e_k = B_δ2lvw_k

где В_δ - магнитная индукция в воздушном зазоре между статором и ротором электрической машины, Тл, v = πD₁n₁/60 = τ2pn₁/60 = 2τf₁ - линейная скорость движения магнитного поля относительно не­подвижной катушки, м/с, πD₁ = τ2p - длина поверхности расточ­ки статора.

С учетом (v = πD₁n₁/60 = τ2pn₁/60 = 2τf₁) мгновенное значение ЭДС катушки

e_k = 4B_δl τf w_k.

Как уже отмечалось, форма кривой ЭДС e_k зависит исключитель­но от графика распределения индукции B_δ в воздушном зазоре. Од­нако график индук­ции является несинусоидальным. Поэтому ЭДС катушки e_k также несинусоидальна и наряду с первой (основной) синусоидальной гармоникой ЭДС содержит ряд высших синусоидальных гармоник.

В связи с тем, что кривая ЭДС симметрична относительно оси абс­цисс, она содержит лишь нечетные гармоники (1,3, и т. д.).

С неко­торым приближением, форму кривой ЭДС e_k можно принять трапецеидаль­ной (рис. 7.5), которая содержит лишь нечетные гармоники (1,3, и т. д.). Исходя из этого можно записать следующее выражение гармоничес­кого ряда:

e = 4E/πα [sinα sinω₁t + 1/3²(sin3α sin3ω₁t) + …],

где Е - амплитуда трапецеидальной ЭДС (см. рис. 7.5); ω1= 2πf₁ - угловая частота основной гармоники.

Рис. 7.5. Разложение трапецеидальной кривой ЭДС в гармонический ряд

Из (e = 4E/πα [sinα sinω₁t + 1/3²(sin3α sin3ω₁t) + …]) видим, что с ростом номера гармоники ЭДС амплитуда этой ЭДС уменьшается пропорционально величине 1/n_г² sinαn_г, а ча­стота f_nг = f₁n_г, т. е. растет пропорционально номеру гармоники. По­этому практическое влияние на форму кривой ЭДС оказывают выс­шие гармоники не выше седьмой. Таким образом, задача получения в обмотке статора синусоидальной ЭДС сводится к устранению или значительному ослаблению высших синусоидальных гармоник, в первую очередь третьей, пятой и седьмой.

Известно, что токи и ЭДС третьей гармоники во всех фазах трех­фазной обмотки совпадают по фазе [см. (1.37)].

Из уравнений токов третьей гармоники для трехфазной системы

i_A3 = I_3maxsin3ωt;

i_B3 = I_3maxsin3(ωt - 120⁰) = I_3maxsin3ωt;

i_C3 = I_3maxsin3(ωt + 120⁰) = I_3maxsin3ωt;

видно, что эти токи в любой момент времени совпадают по фазе, т. е. имеют одинаковое направление.

Поэтому в линей­ной ЭДС (напряжении) при схемах соединения обмоток звездой или треугольником третья гармоника отсутствует.

Автомобильные вентильные генераторы с клювообразным ротором

Автомобильные генераторы переменного тока относятся к синхронным электрическим машинам, а это значит, что частота вра­щения ротора и частота наводимой в обмотках статора Э.Д.С. же­стко связаны между собой.

Вентильный генератор (рис. 53) представляет собой синхронную электрическую машину со встроенным полу­проводниковым выпрямителем.

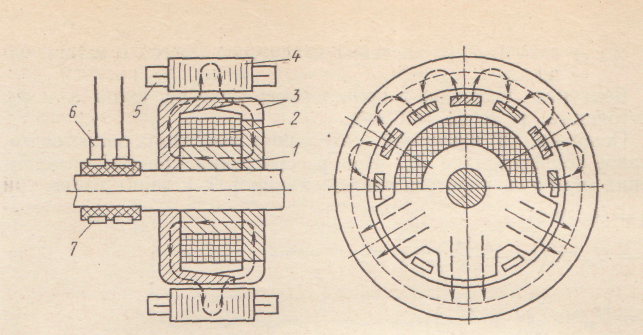
Рис. 53. Конструктивная схема автотракторного синхронного генератора с клювообразным ротором:

1 - втулка; 2 - обмотка возбуждения; 3 - клювообразные полюсы; 4 - пакет статора; 5 - обмотка якоря; 6 - щетки; 7 - контактные кольца

Отличительными особенностями рассматриваемых гене­раторов являются:

1. малая осевая длина;

2. многополюсность;

3. высокая эффектив­ность использования материалов;

4. ротор — клювообразного типа;

5. обмотка возбуждения, состоящая из одной катушки, размещена внутри ротора;

6. малое число пазов на полюс и фазу (обычно q ≤ 1, реже q = 2).

Число пазов на полюс и фазу равно

q = z₁/(2pm),

где z₁ —число пазов статора, а m — число фаз.

Рассмотрим работу вентильного генератора и определим основ­ные соотношения между напряжениями и силами тока на стороне переменного и выпрямленного напряжений.

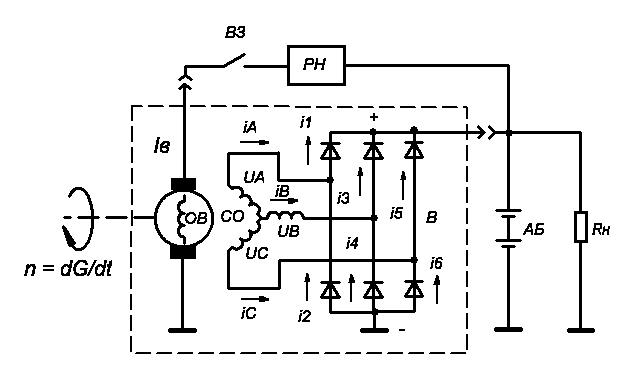
Рис. 5.4. Принципиальная схема вен­тильного генератора

На рис. 54 приведена принципиальная схема вентильного трех­фазного генератора с выпрямителем, собранным по схеме трехфаз­ного двухполупериодного выпрямления.

Принцип действия генератора заключается в следующем. При включе­нии замка зажигания ВЗ на обмотку возбуждения подается напряжение акку­муляторной батареи, которое вызывает появление тока возбуждения. Ток возбуждения, проходя по обмотке возбуждения, создает магнитный поток, рабочая часть которого распределяется по клювообразным полюсам одной полярности. Выходя из полюсов, магнитный поток пересекает воздушный зазор, проходит по зубцам и спинке статора, еще раз пересекает воздушный зазор, входит в клювообразные полюсы другой полярности и замыкается через втулку и вал.

При вращении ротора под каждым зубцом статора проходит поперемен­но то положительный, то отрицательный полюс, т. е. магнитный поток, пересекающий обмотку статора, изменяется по величине и направлению (рис. 1,3).

Рис. 1.3. Изменение во времени t магнитного потока в генераторе переменного тока с клювообразным ротором

При этом в обмотках фазы будет индуцироваться переменная по величине и направлению ЭДС.

Предположим, что магнитный поток, который пересекает обмотки статора, изменяется синусоидально (Рис. 1.3),

Ф = Ф_м sinωt,

продифференцируем по времени оби части уравнения по времени, получим,

dФ/dt = Ф_м dsinωt/dt = Ф_м ω cosωt.

ЭДС наведенная в катушке, в соответствии с законом электромагнитной индукции Фарадея,

u = wdФ/dt

где w – количество витков обмотки статора, следовательно,

u = wФ_мω cosωt = U_мcosωt,

U_м амплитудное значение равно,

U_м = wωФ_м = w2πfФ_м, (ω = 2πf),

а действующее значение,

U_d = U_м/√2 = w2πfФ_м/√2 = 4,44wfФ_м,

где f - частота; w - число витков обмотки одной фазы; Ф_м - магнитный поток.

Частота

f = pn/60,

где p - число пар полюсов; n - частота вращения об/мин.

Действующее значение ЭДС можно переписать в более про­стом виде:

U_d = С_еnФ,

где С_е - постоянный коэффициент равный, С_е = 4,44pw/60.

Обмотка статора генераторов, трехфазные. Она состоит из трех обмоток фаз, которые называют фазными обмотками или фазами, токи и напряжения в которых смещены на 120 электрических градусов. Фазы могут соединяться в «звезду» или «треугольник».

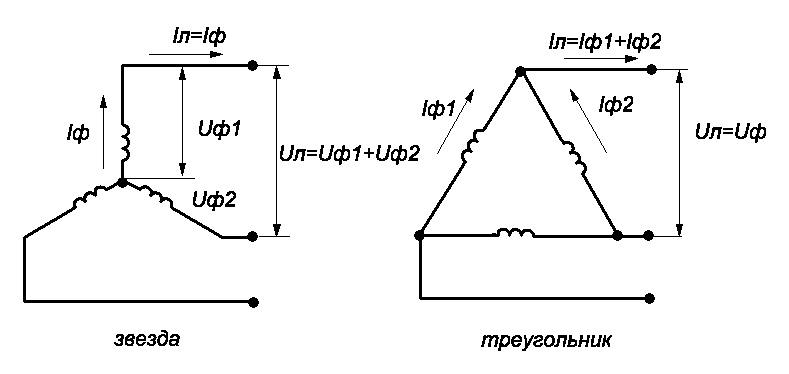
Рис.4.4

При этом различают фазные и линейные напряжения и токи. Напряжение на зажимах фазных обмоток генератора называются фазными напряжениями U_ф, а токи, протекающие в них фазными токами I_ф. При соединении фазных обмоток в «звезду» имеется также напряжение между линейными проводами (соединение обмоток статора с выпрямителем), называемые линейными или междуфазными напряжениями U_л, а токи, протекающие в этих проводах называются линейными токами I_л

U_л = U_Ф√3, I_ф = I_л.

При соединении в «треугольник» фазные токи

I_л = I_ф √3

т.е. токи обмоток в √3 раза меньше линейных токов (токи нагрузки), при соединении в «звезду»

I_л = I_ф.

Это значит, что при одном и том же токе генератора, ток в обмотках фаз при соединении в «треугольник» меньше, чем у «звезды». Поэтому в генераторах большой мощности часто применяют соединение «треугольник», т.к. меньший ток меньше меди. Для того чтобы генератор был способен заряжать АБ и обеспечить питанием других потребителей, требуется преобразовать переменный ток (АС) в постоянный (DС). Такие устройства называются выпрямителями. В автомобильных генераторах наибольшее применение нашли трехфазные мостовые двухполупериодные схемы выпрямления (Рис.5.4).

Рис. 5.4. Принципиальная схема вен­тильного генератора

В этих схемах наиболее благоприятное соотношение между выпрямленной мощностью P_d и мощностью генератора P. Теоретически

P_d = P/1,045.

Схема обеспечивает относительно небольшие пульсации выпрямленного напряжения, что является одним из важных требований к автомобильным генераторам в связи с широким применением электроники.

В рассматриваемом ге­нераторе обмотки статора соединены в звезду. Для этого соедине­ния

U_л = U_Ф√3, I_ф = I_л.

Положим, что нагрузкой вентильного генератора является ак­тивное сопротивление R_н. При этом напряжения фаз равны (Рис. 5.4)

U_A = U_мsin ωt;

U_B = U_мsin (ωt - 2π/3);

U_C = U_мsin (ωt + 2π/3);

где U_м – максимальное значение фазного напряжения; ω = 2πf = 2πpn/60 = πpn/30 – угловая частота вращения.

Положим также, что вентили и их коммутация идеальные (R_пр= 0, R_обр = ∞).

В трехфазной мостовой схеме выпрямления имеется шесть вентилей: в верхней группе вентилей (1, 3, 5) катоды соединены между собой, в нижней группе вентилей (2, 4, 6) соединены между собой аноды. В проводящем направлении работает из верхней группы вентиль, у которого анод имеет наиболее высокий потенциал, а в нижней группе — вентиль, у которого катод имеет наиболее низкий по­тенциал. Следовательно, в любой момент времени работают два вентиля: один положительной полярности (верхний), другой от­рицательной полярности (нижний). Каждый вентиль пропускает ток в течение одной трети периода (T/3).

Рис. 55. Временные диаграммы напряжения и токов вентильного генератора

К выпрямителю подается линейное напряжение генератора. Выпрямленное напряжение U_d пульсирующее, и частота пульсации в 6 раз больше частоты переменного напряжения, т. е. f_п = 6f = 6pn/60 = 0,1pn

Минимальное значение выпрямленного напряжения равно 1,5U_m (U_A +U_C = U_msinπ/6 + U_msin2π/3 = 0,5U_m + 1U_m), а максимальное 1,73U_m (U_B +U_C = U_msinπ/3 + U_msin5π/3 = U_m√3/2 + U_m√3/2 = U_m√3 = U_m1,73). Пульсация выпрямленного на­пряжения,

ΔU_d = (1,73 – 1,5)U_м = 0,23U_м.

Среднее значение выпрямленного напряжения (период пуль­сации Т/6).

По определению среднее значение (постоянная составляющая) равна сумме площади положительной и отрицательной части импульса напряжения или тока деленная на период следования импульсов,

U_d = (S₊ + S_-)/T_и = (S₊ + 0)/T_и = S₊ /T_и.

Период следования выпрямленных импульсов синусоидального напряжения (тока) T_и равен:

1. 2π/6 = π/3 или 60⁰ электрических градусов для двухполупериодного трехфазного выпрямителя.

Пощадь выпрямленных импульсов напряжения равена:

1. S₊ = ∫U_л cosωt dωt = U_л (sinωt) = U_л (sin π/6 – (sin -π/6)) = U_л (1/2 – (- 1/2)) = U_л (1) = U_м√3, (предел интегрирования от – π/6 до +π/6, переместили начало координат в точку π/2, поэтому sin заменили на cos).

Постоянная составляющая выпрямленного напряжения равна:

1. U_d = √3U_м /T_и = √3U_м/(π/3) = 3√3 U_м /π = 1,65U_м.

При определении интеграла необходимо иметь в виду, что ω = 2π/T.

Пульсацию выпрямленного напряжения можно выразить через среднее значение выпрямленного напряжения,

ΔU_d = 0,23U_м, U_d = 1,65U_м, U_м = U_d/1,65, ΔU_d = 0,23U_d/1,65.

Так, например, при среднем значении выпрямленного напря­жения 14 В пульсация равна 1,95 В. При этом максимальное зна­чение выпрямленного напряжения равно 14,65 В, а минимальное 12,7 В.

При подключении к выпрямителю активной нагрузки R_н про­текает ток

I_d = U_d/R_н.

Следовательно, форма выпрямленного тока имеет такой же вид, как и выпрямленное напряжение.

Среднее значение выпрямленного тока

I_d = (3/π) ∫I_dm cosωt dωt = (3/π) I_dm (sinωt) = (3/π)I_dm (sin π/6 – sin -π/6) =

(3/π)I_dm = 0,955I_dm,

(предел интегрирования от – π/6 до +π/6, переместили начало координат в точку π/2, поэтому sin заменили на cos).

Каждый диод пропускает ток в течение одной трети периода (Т/3). Поэтому токи i₁, i₂, i₃, i₄, i₅, i₆ имеют пульсирующий характер (рис. 55). Среднее значение тока одного диода равно I_d/3.

Действующее значение фазного тока. Действующее значение фазного тока важно знать на том основании, что тепловое действие тока пропорционально квадрату тока или напряжения.

Действующее значение тока I_д – это среднеквадратичное значение за период переменного тока.

I_д = √ (i²) _ср = √ (S_ср.²/T) ,

где S_ср² значение суммы квадратов площадей сигнала за период (S²₊ + S²_-),

Т - период частоты сигнала.

Для косинусоидального тока квадрат площади за период равен,

S² = ₀∫^2π I²_m cos² ωt dωt = I²_m π.

Период частоты сигнала равен 2π.

Среднеквадратическое значениями значение косинусоидального тока равно,

I_ср.кв. = √ (I²_mπ /2π) = I_m/√2 = 0,707I_m.

Среднеквадратическое значение сигнала переменного тока зависит от его формы. Так, среднеквадратическое значение синусоидального сигнала составляет 0,707 его пикового значения (амплитуды). Это справедливо только для синусоидального сигнала.

Среднеквадратиче­ское значение сигналов, имеющих другую форму, может быть определено следующим образом:

1. определяем квадрат площади положительной части сигнала за один период,

S²₊ = U²₊×t₊;

2. определяем квадрат площади отрицательной части сигнала за один период. Заметим, что при опре­делении площади отрицательное значение превращается в положи­тельное,

S²_- = U²_-×t_-;

3. определяем среднее значение суммарной площади сигнала за период

(S²₊ + S²_-) /T;

4. вычисляем квадратный корень из средней площади сигнала за период

U_д = √[(S²₊ + S² _-) /T].

Токи, протекающие по фазным обмоткам генератора, имеют несинусоидальный преры­вистый характер из (рис.55), видно, что кривая тока фазный обмотки генератора содержит четыре одинаковые части длительностью Т/6 каждая.

Определим действующее значение фазного тока.

1. определяем среднее значение квадрата площади фазного тока за период

(S²₊ + S²_-) /T = 4(_-π/6∫^+π/6I_dm²cos²ωtdωt)/2π = 2I_dm²/π(ωt/2 + 1/4sin2ωt) =

= 2I_dm²/π [π/12 + 1/4sinπ/3 – (- π/12 + 1/4sin - π/3)] =

= 2 I_dm²/π (π/6 + √3/4) = I_dm²0,6;

2. вычисляем квадратный корень из средней площади сигнала за период

I_дф = √ I_d²0,6 = I_dm 0,775.

Обычно при определении действующего значения фазного тока полагают, что форма фазного тока прямоугольная и имеет ампли­туду, равную среднему значению выпрямленного тока I_d. В этом случае:

1. (S²₊ + S²_-) /T = (4I_d²T/6)/T = (2I_d²/3);

2. I_dф = I_d√2/3 = I_d0,816.

Сравнение показывает, что погрешность невелика.

При рассмотрении соотношений напряжений и токов вентиль­ного генератора следует учитывать, что полупроводниковые вен­тили (диоды) не являются идеальными (рис. 56). Ток закрывающего диода исчезает не мгновенно, а ток открывающего диода нарастает постепенно.

Рис. 56. Вольт - амперные характе­ристики диода

С достаточной для инженерных расчетов точ­ностью диод замещается моделью из простейших линейных элементов. На рис. 56 показана прямая ветвь ВАХ диода (линия 1) и аппроксимирующий эту ветвь отрезок прямой 2. Уравнение линейной аппроксимации имеет вид:

U_d = U_o + R_диф.пр I_{д. пр},

где R_диф.пр - дифференциальное сопротивление диода при прямом смещении, U_o - пороговое напряжение.

Для диодов, применяемых в автотракторном электрооборудо­вании, пороговое напряжение U₀ = 0,8 -1,0 В.

Для определения величины R_{диф. пр} необходимо выбрать на аппроксимирующей прямой (прямая 2 на рис. 56) две произвольные точки (одна из них может лежать на оси напряжения). Для этих точек нужно найти разность напряжений и разность токов, а затем разделить первую разность на вторую,

R_диф.пр = ΔU/ΔI.

Выходными параметрами вентильного генератора являются:

1. среднее значение выпрямленного напряжения U_d;

2. среднее значение выпрямленного тока I_d;

3. выпрямленная мощность P_d = U_dI_d.