21.Двугранный угол. Признак перпендикулярности двух плоскостей

Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями .Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней. Линейный угол между этими двумя лучами и будет равен по величине двугранному углу. Если один из лучей не перпендикулярен ребру, то величина линейного угла между лучами в общем случае будет отлична от величины двугранного угла. Например, в любой двугранный угол (в том числе больший 90 градусов) можно поместить прямой угол так, чтобы его вершина лежала на ребре двугранного угла, а стороны принадлежали его граням. В этом легко убедиться, размещая угольник в приоткрытой книг

ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство: Пусть   - плоскость , b - перпендикулярная ей прямая,  - плоскость проходящая через прямую b, и с - прямая по которой пересекаются плоскости   и  . Докажем, что плоскости   и  перпендикулярны. Проведем в плоскости   через точку пересечения прямой b с плоскостью  прямую а, перпендикулярную прямой с. Проведем через прямые а и bплоскость  . Она перпендикулярна прямой с, так как прямые а и bперпендикулярны, то плоскости   и   перпендикулярны. Теорема доказана. 

22.Призмы. Виды призм. Площадь поверхности

Призма - это многогранник, две грани которого - одноименные многоугольники, лежащие в параллельных плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны

Если боковые ребра призмы перпендикулярны к плоскости основания, то — призма прямая. Если нет — призма наклонная. Если в прямой призме основание — правильный многоугольник — призма правильная.

1. Основания призмы являются равными многоугольниками

2. Боковые ребра призмы равны

3. Боковые грани призмы являются параллелограммами.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой стороны призмы – сумма площадей ее боковых граней. Площадь Sполн полной поверхности выражается через площадь Sбок боковой поверхности и площадь Sосн основания призмы формулой

Sполн=Sбок+2Sосн

23.Параллелепипед. Виды и свойства

Параллелепипед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм. Типы параллелепипедов Параллелепипеды, как и призмы, могут быть прямыми и наклонными. Прямым параллелепипедом называется прямая призма, основание которой — параллелограмм. Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники. Моделями прямоугольного параллелепипеда служат классная комната, кирпич, спичечная коробка. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями. Например, имеются спичечные коробки с измерениями 15, 35, 50 мм Куб — прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты. Свойства Параллелепипед симметричен относительно середины его диагонали, соединяющей противоположные вершины. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Противолежащие грани параллелепипеда параллельны и равны. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. Аффинное преобразование всегда переводит параллелепипед в параллелепипед. Для любого параллелепипеда существует аффинное преобразование, которое преобразует его в куб.

222222

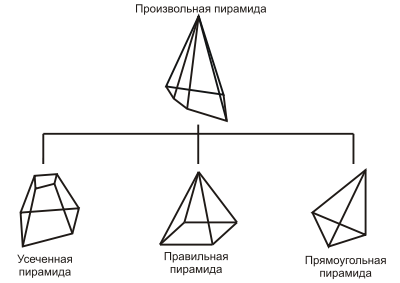
Пирамида. Виды пирамид. Сечение пирамиды

Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину^[1]. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.