
- •3. Экстремумы функции. Исследование функции на экстремум с помощью первой производной.
- •4. Наибольшее и наименьшее значение функции на отрезке.
- •5. Асимптоты. Схема построения графика функции
- •6.Первообразная. Неопределенный интеграл, его свойства
- •7. Основные табличные интегралы
- •Неопределенный интеграл степенной функции
- •Неопределенный интеграл експоненты показательной функции
- •8. Интегрирование способом подстановки
- •9.Определеный интеграл.Геометрический смысл
- •10. Вычисление площадей плоских фигур через определенный интеграл
- •12.Деление отрезка в данном отношении.
- •Операции над векторами в прямоугольной системе координат.
- •13. Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
- •14.Уравнение прямой в отрезках.
- •15.Взаимное расположения прямых.
- •16.Угол между прямыми
- •17.Аксиомы стереометрии
- •18.Признак параллельности двух плоскостей
- •20.Перпендикуляр и наклонные к плоскости. Теорема о трех перпендикулярах
- •21.Двугранный угол. Признак перпендикулярности двух плоскостей
- •22.Призмы. Виды призм. Площадь поверхности
- •23.Параллелепипед. Виды и свойства
- •25.Площадь поверхности пирамиды
- •26.Усеченная пирамида. Площадь ее поверхности
- •31.Конус. Усеченный конус. Площадь поверхности конуса и усеченного конуса
- •36.Кривые второго порядка
Операции над векторами в прямоугольной системе координат.
С векторами, заданными в прямоугольной системе координат совершать действия еще проще, чем с их геометрическими образами. В этой статье мы покажем как выполняются операции сложения векторов и умножения вектора на число, если известны их координаты, и подробно разберем решения примеров.
Пусть
на плоскости задана прямоугольная
декартова система координат Oxy.
Рассмотрим векторы ![]() и
и ![]() .
Эти векторы можно разложить по
координатным векторам
.
Эти векторы можно разложить по
координатным векторам ![]() и
и ![]() как
как ![]() и
и ![]() ,
что было показано в
,
что было показано в
13. Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
Вывод [показать]
![]()
где ![]() —
координаты
—
координаты ![]() и
и ![]() направляющего
вектора прямой,
направляющего
вектора прямой, ![]() и
и ![]() координаты
точки, принадлежащей
прямой.
координаты
точки, принадлежащей
прямой.
Параметрические уравнения прямой могут быть записаны в виде:
![]()
где ![]() —
производный параметр,
—
производный параметр, ![]() —
координаты
и
направляющего
вектора прямой. При этом
—
координаты
и
направляющего
вектора прямой. При этом
![]()
![]()
Смысл параметра аналогичен параметру в векторно-параметрическом уравнении.
Уравнение прямой, проходящей через две заданные несовпадающие точки
Если
заданы две несовпадающие точки с
координатами ![]() и
и ![]() ,
то прямая, проходящая через них, задаётся
уравнением
,
то прямая, проходящая через них, задаётся
уравнением

или
![]()
или в общем виде
![]()
14.Уравнение прямой в отрезках.
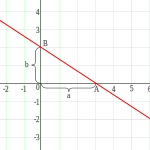
Уравнение
прямой линии, пересекающей ось ![]() в
точке
в
точке ![]() и
ось
и
ось ![]() в
точке
в
точке ![]() :
:
![]()
В этом виде невозможно представить прямую, проходящую через начало координат.
15.Взаимное расположения прямых.
Три
точки
,
и ![]() лежат
на одной прямой тогда и только тогда,
когда выполняется условие
лежат
на одной прямой тогда и только тогда,
когда выполняется условие

Отклонение точки
от
прямой ![]() может
быть найдено по формуле
может
быть найдено по формуле![]()
где
знак перед радикалом противоположен
знаку ![]() Отклонение
по модулю равно расстоянию
между точкой и прямой;
оно положительно, если точка и начало
координат лежат по разные стороны от
прямой, и отрицательно, если по одну
сторону.
Отклонение
по модулю равно расстоянию
между точкой и прямой;
оно положительно, если точка и начало
координат лежат по разные стороны от
прямой, и отрицательно, если по одну
сторону.
16.Угол между прямыми
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
17.Аксиомы стереометрии
Признаки параллельности прямой и плоскости
Стереометрия - раздел геометрии, в котором изучаются фигуры в пространстве.
Аксиома 1.1. Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Аксиома 1.2. Если две разные плоскости имеют общую точку, то они имеют и общую прямую, проходящую через эту точку.
Аксиома 1.3. Если две разные прямые имеют общую точку, то через них можно провести плоскость, и притом единственную.
Аксиома 1.4. Для произвольной плоскости выполняются аксиомы планиметрии
Теорема
Если
прямая, не принадлежащая плоскости,
параллельна какой-нибудь прямой в этой
плоскости, то она параллельна и самой
плоскости.
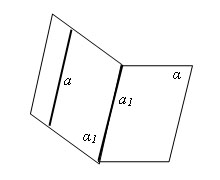 Доказательство
Пусть
α - плоскость, a – не лежащая в ней прямая
и a1 – прямая в плоскости α, параллельная
прямой a. Проведем
плоскость α1 через прямые a и a1. Плоскости
α и α1 пересекаются по прямой a1. Если бы
прямая a пересекала плоскость α, то
точка пересечения принадлежала бы
прямой a1. Но это невозможно, так как
прямые a и a1 параллельны. Следовательно,
прямая a не пересекает плоскостью α, а
значит, параллельна плоскости α. Теорема
доказана.
Доказательство
Пусть
α - плоскость, a – не лежащая в ней прямая
и a1 – прямая в плоскости α, параллельная
прямой a. Проведем
плоскость α1 через прямые a и a1. Плоскости
α и α1 пересекаются по прямой a1. Если бы
прямая a пересекала плоскость α, то
точка пересечения принадлежала бы
прямой a1. Но это невозможно, так как
прямые a и a1 параллельны. Следовательно,
прямая a не пересекает плоскостью α, а
значит, параллельна плоскости α. Теорема
доказана.
