11) Рекурсивный способ моделирования иерархий средствами реляционной субд. Проблема поиска листьев.
Классически проблема представления иерархий решается с помощью рекурсивной связи, что позволяет хранить в одной таблице дерево любой глубины и размерности.
Таблицу можно создать следующим предложением SQL:
CREATE TABLE T (Id INT NOT NULL IDENTITY PRIMARY KEY,
Parent INT NOT NULL REFERENCES T(Id),
Data VARCHAR);
Список узлов, не имеющих потомков, получаем как выборку имѐн узлов, не входящих в список узлов, являющихся предками других узлов (рис. 14):
SELECT DISTINCT Id, Data FROM T
WHERE Id NOT IN (SELECT DISTINCT Parent FROM T);
Другой вариант запроса с таким же результатом, но с использованием EXIST:
SELECT * FROM T AS E1 WHERE NOT EXISTS
(SELECT * FROM T AS E2 WHERE E1.Id=E2.Parent);
12) Нормализация, основное назначение. Что оптимизирует нормализация?
Процесс нормализации это последовательное преобразование исходной БД к НФ, при этом каждая следующая НФ обязательно включает в себя предыдущую (что, процесс на этапы и производить его однократно, не возвращаясь к предыдущим этапам).
Всего в реляционной теории насчитывается 6 НФ:
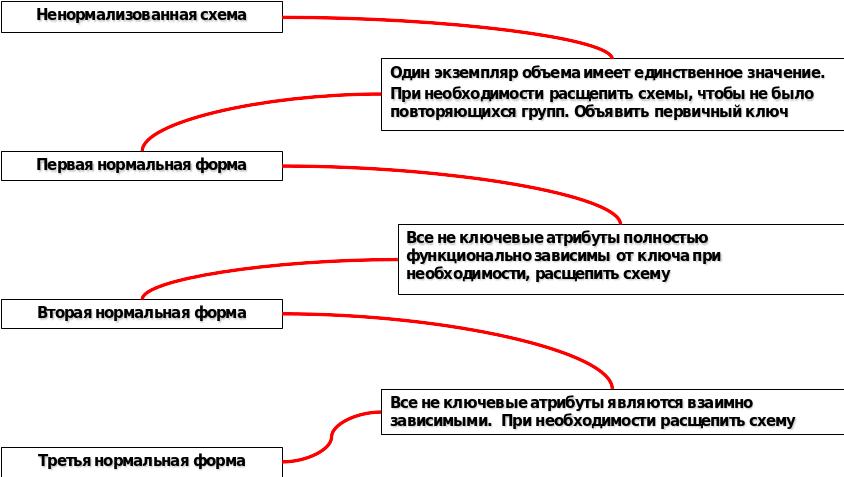
Первая нормальная форма (обычно обозначается также 1НФ).
Вторая нормальная форма.
Третья нормальная форма.
нормальная форма Бойса-Кодда (НФБК).
Четвёртая нормальная форма.
Пятая нормальная форма, или нормальная форма проекции-соединения (5NF или PJ/NF) .
На практике, как правило, ограничиваются 3НФ, ее оказывается вполне достаточно для создания надежной схемы БД. НФ более высокого порядка представляют скорее академический интерес из-за их сложности. Более того, при реализации абстрактной схемы БД в виде реальной базы иногда разработчики вынуждены сделать шаг назад – провести денормализацию с целью повышения эффективности, т.к. идеальная, с точки зрения теории, структура может оказаться слишком накладной на практике.
13) Моделирование сложных структур средствами реляционной СУБД. 3 способа моделирования деревьев.
2.1. Рекурсивный способ представления иерархии
Классически проблема представления иерархий решается с помощью рекурсивной связи, что позволяет хранить в одной таблице дерево любой глу-бины и размерности.
2.2. Способ правого и левого коэффициентов
Метод, предложенный Джо Селко, называемый ещѐ методом вложен-ных множеств, основан на полном обходе дерева (рис. 43). При полном обходе дерева каждому узлу назначается пара значений – левый и правый коэффици-енты. Левые коэффициенты присваиваются во время движения от предка к по-томку. Правые коэффициенты назначаются при движении от потомка к предку.
2.3. Способ вспомогательной таблицы
Способ, описанный Ральфом Кимбаллом, может рассматриваться как расширенный вариант рекурсивного способа. Здесь модель дерева строится на основе двух таблиц. Первая таблица (базовая) хранит список всех узлов, снаб-жѐнных уникальными идентификаторами, и всю содержательную информацию по каждому узлу.
Билет №29. 1) Регулярные выражения. Основные понятия. Шаблоны регулярных выражений.
Регуля́рные выраже́ния (англ. regular expressions, сокр. RegExp, RegEx, жарг. регэ́кспы или ре́гексы) — это формальный язык поиска и осуществления манипуляций с подстроками в тексте, основанный на использовании метасимволов (символов-джокеров, англ. wildcard characters). По сути это строка-образец (англ. pattern, по-русски её часто называют «шаблоном», «маской»), состоящая из символов и метасимволов и задающая правило поиска.
Регулярные выражения произвели прорыв в электронной обработке текстов в конце XX века. Набор утилит (включая редактор sed и фильтр grep), поставляемых в дистрибутивах UNIX, одним из первых способствовал популяризации регулярных выражений для обработки текстов. Многие современные языки программирования имеют встроенную поддержку регулярных выражений. Среди них Perl, Java[1], PHP, JavaScript, языки платформы .NET Framework[2], Python, Tcl, Ruby и др.
Регулярные выражения используются некоторыми текстовыми редакторами и утилитами для поиска и подстановки текста. Например, при помощи регулярных выражений можно задать шаблоны, позволяющие:
найти все последовательности символов «кот» в любом контексте, как то: «кот», «котлета», «терракотовый»;
найти отдельно стоящее слово «кот» и заменить его на «кошка»;
найти слово «кот», которому предшествует слово «персидский» или «чеширский»;
убрать из текста все предложения, в которых упоминается слово кот или кошка.
Регулярные выражения позволяют задавать и гораздо более сложные шаблоны поиска или замены.
Обычные символы (литералы) и специальные символы (метасимволы)
Большинство символов в регулярном выражении представляют сами себя за исключением специальных символов [ ] \ ^ $ . | ? * + ( ) { }, которые могут быть предварены символом \ (обратная косая черта) («экранированы», «защищены») для представления их самих в качестве символов текста. Можно экранировать целую последовательность символов, заключив её между \Q и \E.
Метасимвол . (точка) означает один любой символ, но в некоторых реализациях исключая символ новой строки.
Символьные классы (наборы символов)
Набор символов в квадратных скобках [ ] именуется символьным классом и позволяет указать интерпретатору регулярных выражений, что на данном месте в строке может стоять один из перечисленных символов. В частности, [абв] задаёт возможность появления в тексте одного из трёх указанных символов, а [1234567890] задаёт соответствие одной из цифр. Возможно указание диапазонов символов: например, [А-Яа-я] соответствует всем буквам русского алфавита, за исключением букв «Ё» и «ё».[5]
Если требуется указать символы, которые не входят в указанный набор, то используют символ ^ внутри квадратных скобок, например [^0-9] означает любой символ, кроме цифр.
Позиция внутри строки
Следующие символы позволяют спозиционировать регулярное выражение относительно элементов текста: начала и конца строки, границ слова.
Представление Позиция
^ Начало строки
$ Конец строки
\b Граница
\B Не граница слова
\G Предыдущий успешный поиск
Квантификация (поиск последовательностей).
Квантификатор после символа, символьного класса или группы определяет, сколько раз предшествующее выражение может встречаться. Следует учитывать, что квантификатор может относиться более чем к одному символу в регулярном выражении, только если это символьный класс или группа.
Представление Число повторений
{n} Ровно n раз
{m,n} От m до n включительно
{m,} Не менее m
{,n} Не более n
Представление Число повторений Эквивалент
* Ноль или более {0,}
+ Одно или более {1,}
? Ноль или одно {0,1}