15.Косплексное представление синусоидальных электрических величин.

Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.

Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис. 3.3. Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:

Алгебраической

U = U’+ jU"

I = I’ – jI",

где U', U", I', I" – проекции векторов на оси действительных и мнимых чисел.

Показательной

U=U*e^(j*ψ_u)

I=I*e^(j*ψ_i)

где U, I – модули (длины) векторов; е – основание натурального логарифма; e^(j*ψ_u) и e^(j*ψ_i) - поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.

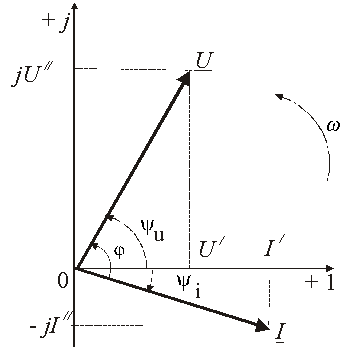Рис. 3.3 – Представление синусоидальных напряжения и тока векторной диаграммой на комплексной плоскости

Тригонометрической

U = U·(cosψ_u + jsinψ_u)

I = I·(cosψ_i – jsinψ_i).

При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера

е^j·ψ = cosψ + jsinψ.

17. Активная, реактивная и полная мощности.

Р = UrI = I2r — активная мощность цепи, Вт, кВт;

QL = ULI = I2xL —реактивная индуктивная мощность цепи, обусловленная энергией магнитного поля, вар, квар;

QС = UСI = I2хС — реактивная емкостная мощность цепи, обусловленная энергией электрического поля, вар, квар);

Q = QL - QС = I2x — реактивная мощность цепи, вар, квар ,это та мощность, которой приемник обменивается с сетью;

S = UI = I2z — полная мощность цепи. В • А, кВ • А (рис. 2.9, г, 2.10, г, 2.11, г и ж);

cos φ = r/z = P/S—коэффициент   мощности   цепи   (рис.   2.9, г, 2.10, г, 2.11, г и ж).

Из треугольников мощностей можно установить следующие связи между Р, Q, S и cos φ:

P = S cos φ = UI cos φ; Q = S sin φ = UI sin φ; S = √P2 + Q2 = UI .

За единицу активной мощности принят ватт (Вт) или киловатт (кВт), реактивной мощности — вольтампер реактивный (вар) или киловольтампер реактивный (квар), полной мощности — вольтампер (ВА) или киловольтампер (кВ•А).

Реактивные (индуктивная, емкостная) мощности, обусловленные соответственно энергией магнитного поля индуктивности и электрического поля емкости, не совершают никакой полезной paботы, однако они оказывают существенное влияние на режим работы электрической цепи. Циркулируя по проводам трансформаторов, генераторов, двигателей, линий передач, они нагревают их. Поэтому расчет проводов и других элементов устройств переменного тока производят, исходя из полной мощности S, которая учитывает активную и реактивную мощности.

19.Резонанс напряжений в последлвательной цепи r,l,c.

Так как сопротивления конденсатора и катушки индуктивности зависят от частоты колебаний тока в цепи, то и полное сопротивление Z также будет изменяться при изменении .

Если  = 0, то R_C = 1/C =  и, следовательно, Z = , а ток в цепи равен нулю. Действительно, постоянный ток не проходит через конденсатор, между пластинами которого располагается диэлектрик. С увеличением  сопротивление Z уменьшается и принимает минимальное значение Z_min = R при частоте _о, определяемой условием ω₀L-1/(ω₀C)=0, откуда ω₀=1/√(LC)

При дальнейшем увеличении частоты сопротивление Z вновь будет увеличиваться, а амплитуда тока - уменьшаться, асимптотически прибли-жаясь к нулю при   .

Частота _о называется резонансной частотой. При  = _о амплитудное значение тока в цепи достигает максимального значения I_0max =U₀/R. Напряжения на катушке индуктивности и конденсаторе в этот момент равны,по,величине:U_co=I_0maxR_c=U₀/Rω₀C=U₀/R*√(L/C)=QU_{0 ULO=IOmaxRL=(UCωOL)/R=(UO*√(L/C))/R=UOρ/R=QUO}

.

Величина ρ=_√L/C называется волновым сопротивлением, а величина Q=ρ/R – добротностью RLC-цепи. Если ρ>R, то в момент резонанса амплитуды напряжений на индуктивности и емкости превышают амплитуду общего напряжения, приложенного к RLC-цепи U_o. Однако, как видно из векторной диаграммы (рис. 7), в момент резонанса фазы колебаний напряжения на емкости и индуктивности противоположны и сумма этих напряжений равна нулю. Напряжение на резисторе при этом равно общему напряжению, приложенному к RLC-цепи: U_RO=I_OmaxR=U_O