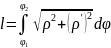- •Что такое дифференциальное уравнение и его решение ? Примеры задач, приводящих к дифференциальным уравнениям (задача о радиоактивном распаде и задача о колебании груза напружине).
- •Линейные дифференциальные уравнения первого порядка, Метод вариации произвольной постоянной. Уравнения Бернулли.
- •Однородные дифференциальные уравнения первого порядка.
- •Задача Коши и теорема Коши для дифференциального уравнения порядка n (формулировка). Общее решение дифференциального уравнения.
- •Линейные дифференциальные уравнения (второго порядка). Линейность пространства решений однородного уравнения.
- •Теорема о связи первообразных одной и той же функции. Определение неопределенного интеграла.
- •Взаимная обратность операций интегрирования и дифференцирования. Свойство линейности неопределенного интеграла.
- •Задачи о вычислении площади криволинейной трапеции и нахождении длины пути по известной скорости.
- •Определение определенного интеграла. Теорема существования (формулировка). Геометрический и механический смысл интеграла.
Теорема о связи первообразных одной и той же функции. Определение неопределенного интеграла.
Первообразной функции f(x) на некотором (конечном или бесконечном) интервале называется дифференцируемая функция F(х), производная которой равна f(x) во всех точках интервала, т.е. F'(х) = f(x).
Теорема.
Пусть
 и
и
 - первообразные для
,
тогда они отличаются друг от друга на
постоянные слагаемые(const),т.е.
- первообразные для
,
тогда они отличаются друг от друга на
постоянные слагаемые(const),т.е.
 .
.
Док-во.
1.
По условию
 и
и

2.

 , т.е.
, т.е.
Неопределённым
интегралом
 функции
называется множество всех её первообразных.
функции
называется множество всех её первообразных.

Для проверки формулы достаточно найти производную функции F(х) и убедиться в том, что она равна подынтегральной функции f(х).
Взаимная обратность операций интегрирования и дифференцирования. Свойство линейности неопределенного интеграла.
Интегрирование и дифференцирование есть две взаимно обратные операции. Всякому правилу дифференцирования соответствует правило (метод) интегрирования. Так, свойство линейности производной переходит в свойство линейности интеграла. Правилу дифференцирования сложной функции соответствует, как мы видели, метод интегрирования введением под знак дифференциала. Этому же правилу соответствует также метод интегрирования заменой переменной. И правилу дифференцирования произведения соответствует метод интегрирования по частям.
Свойство линейности: интеграл от линейной комбинации функций равен линейной комбинации от интегралов этих функций.
Задачи о вычислении площади криволинейной трапеции и нахождении длины пути по известной скорости.
1)Вычисление
площадей криволинейных трапеций. Из
геометрического
смысла
определенного интеграла следует, что
площадь криволинейной трапеции,
т.е.
области,
лежащей
под графиком
функции
 ,
,
 ,
вычисляется по формуле
,
вычисляется по формуле
 .
.
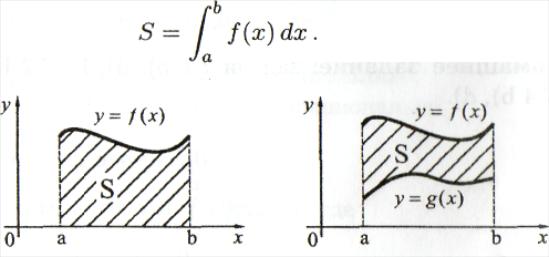
Площадь области S, расположенной между графиками двух функций, т.е. S : а ≤ х ≤ b, g(х) ≤ у ≤ f(х), вычисляется по формуле

2)Пусть мат. точка движется по прямой(оси x) с известной переменной скоростью dt от d=a до d=b. Требуется найти расстояние S, которое проходит точка.
 ,
тогда
,
тогда

Разобьем
время движения на части

Рассмотрим
промежуток времени.
 ,
тогда за время от
,
тогда за время от
 до
до
 мы можем считать приближенно, что мы
едем с постоянной скоростью. При этом
проходим расстояние
мы можем считать приближенно, что мы
едем с постоянной скоростью. При этом
проходим расстояние
 ,
,


Определение определенного интеграла. Теорема существования (формулировка). Геометрический и механический смысл интеграла.
Определённым интегралом от функции f(x) по отрезку [a,b] , или в пределах от a до b, называется предел интегральных сумм при стремлении диаметра разбиения к нулю:

Теорема существования определённого интеграла. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема по этому отрезку.
Геометрически
интегральная сумма представляет из
себя площадь ступенчатой фигуры,
сост-щей из прямоугольников, в основании
которых лежат отрезки ∆xi,
а высоты равны f(ci),
если f(x)≥0
Механический смысл опред. интеграла. Если переменная- это время, а функция – это скорость, то интеграл скорости по времени равен расстоянию.

Свойства определенного интеграла.
1)Если
функция интегрируема на ,
то она интегрируема на любом отрезке
,
то она интегрируема на любом отрезке

2)
Аддитивность.
Для любых a,
b
и c

3)
Линейность. Интеграл
обладает свойством линейности: для
любых функций
 и любой постоянной A
и любой постоянной A


4)
Если
 интегрируемы на [a; b], то
интегрируемы на [a; b], то
 также интегрируема на этом отрезке.
также интегрируема на этом отрезке.
5)
Интегрирование
неравенств.
Если ,
то
,
то
 .
В частности, если
.
В частности, если ,
то
,
то

6)
Если
для любого
 и существует
и существует
 такое, что
такое, что
 причем
непрерывна в x0
то
причем
непрерывна в x0
то

7) Если поменять местами пределы интегрирования, то интеграл изменит знак.

8)
Если
непрерывна на
,
то
 точка
такая, что
точка
такая, что

Теорема (Барроу) о дифференцировании определенного интеграла по переменному верхнему пределу.
Если
непрерывна, то
 имеет производную, которая равна
подынтегральной функции.
имеет производную, которая равна
подынтегральной функции.
Док-во.

 ,т.е.
,т.е.

Следствие. Теорема утверждает, что является первообразной . Т.О. У каждой непрерывной функции есть первообразная.
Формула Ньютона-Лейбница.
Если
функция
непрерывна на
и
 – её первообразная, то
– её первообразная, то

Замена переменных в определенном интеграле.
Пусть функция непрерывна на [a;b], а функция
 непрерывно
дифференцируема на отрезке
непрерывно
дифференцируема на отрезке ,
причем
,
причем ,
и значения функции
,
и значения функции
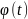 не выходят за пределы отрезка [a;b],
когда
не выходят за пределы отрезка [a;b],
когда
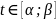 .
Тогда
.
Тогда

Интегрирование по частям для неопределенного и определенного интеграла

Для
определенного интеграла.
Если функция
 непрерывно дифференцируемы на отрезке
[a;b],
то
непрерывно дифференцируемы на отрезке
[a;b],
то

Вычисление площади криволинейного сектора в полярных координатах.
Площадь
криволинейного сектора, ограниченного
кривой, заданной в полярных координатах
уравнением
 и
двумя лучами
и
двумя лучами
 ,
определяется по формуле
,
определяется по формуле

Длина дуги кривой. Вычисление длины дуги графика функции.
Если
существует
 и этот предел не зависит от способа
разбиения отрезка
и этот предел не зависит от способа
разбиения отрезка
 на кусочки, то он называется длиной
дуги кривой AB.
на кусочки, то он называется длиной
дуги кривой AB.
Элемент
длины дуги кривой dl
находится по теореме Пифагора:
 .
.
Если
гладкая прямая является графиком
функции
,
 то
её длина l
равна
то
её длина l
равна

Вычисление длины дуги кривой, заданной параметрически и в полярной системе координат.
Если кривая задана параметрическими уравнениями х =x(t), y=y(t), α≤t≤β, то

Если
кривая задана в полярных
координатах уравнением
,
 ,
то
,
то