матан

1.

Основные понятия теории вероятностей

Основным понятием теории вероятностей является событие. Как и всякому основному понятию, событию не может быть дано строгое определение, но оно может быть пояснено на примерах.

Приведем их.Подбрасываются 3 игральные кости. Выпадение в сумме 14 очков — это событие.Парашютист готовится к прыжку. Тот факт, что парашют раскроется — событие.Студент отправляется на зачет. То, что он сдаст (не сдаст) зачет — это событие.Из колоды вынимаются 3 карты. То, что мы при этом вытянем тройку, семерку и туза — это тоже событие.Различные события можно классифицировать следующим образом.

1. Невозможное событие — событие, которое не может произойти ни при каких испытаниях.

2. Достоверное событие — событие, которое обязательно произойдет при любом испытании.

3. Случайное событие — событие, которое может произойти, а может не произойти.

Пример 1.1Бросают 2 кубика.Невозможное событие: сумма цифр равна 1, сумма цифр больше 13 и т.п.Достоверное событие: сумма цифр больше 1 и меньше 13.Случайное событие: сумма цифр меньше 5, сумма цифр больше 7 и т.п.Дадим несколько определений, относящихся к случайным событиям.

Определение. Несовместными называются события, в которых появление одного события исключает появление другого события.Пример 1.2Бросают кубик. Выпадение 2 исключает выпадения 1, 3 и т.д. События, когда выпало 1, 2, 3 и т.д., — несовместны. А, например, два события — выпало 3 и выпало число очков меньше 5 — совместны, так как выпадение 3 очков укладывается и в категорию «меньше 5».

Определение. События образуют полную группу событий, если в результате испытания появляется хотя бы одно из них.Пример 1.3Бросают кубик. Шесть событий (выпали 1, 2, 3, 4, 5, 6) образуют полную группу, так как одно из этих событий обязательно произойдет.

Пример 1.4Бросают кубик. Два события (выпадет число, меньшее 5, и выпадет число, большее двух) образуют полную группу событий

.Замечание. В задачах по теории вероятности часто неявно предполагаются выполненными ряд очевидных условий. Так, в предыдущем примере неявно предполагается, что кубик встать на ребро или повиснуть в воздухе не может.

Определение. События называются равновозможными (равновероятными), если при большом числе испытаний частота их появления одинакова.

Пример 1.5Равновозможные события — это «орел — решка» при подбрасывании монеты; выпадения 1, 2, 3, 4, 5, 6 при подбрасывании кубика. Неравновозможные события: выпадение числа очков больше 1, между 4 и 6, равного 2 при подбрасывании кубика; оценки 2, 3, 4, 5 на экзамене

.Определение. Событие называется элементарным, если оно не разделимо на более простые.

Пример 1.6Шесть событий (выпали 1, 2, 3, 4, 5, 6) — элементарные, а событие —выпало число очков меньше 4 — не элементарное, так как разложимо на более простые: выпало 1, 2, 3.

Определение. Множество всех элементарных событий, которые могут появиться в испытаниях, называется пространством элементарных событий и обозначается символом Ω.Очевидно, что все элементарные события попарно несовместны.

2.

Классическое и статистическое определение вероятностей

Существуют классическое и статистическое определение вероятности события. Их основное отличие друг от друга состоит в том, что классическое определение вероятности основывается исключительно на умозаключениях и не предполагает проведения какого бы то ни было эксперимента, в то время как статистическое определение вероятностей, наоборот, не связано ни с какими рассуждениями, а основывается только лишь на проводимых многочисленных испытаниях. Кажущееся на первый взгляд принципиальное отличие этих двух понятий вероятностей на самом деле не так значительно, поскольку в основу умозаключений классического определения вероятностей положен огромный предшествующий опыт. Рассмотрим каждое из этих определений вероятностей.

Классическое определение вероятности. Когда мы хотим дать количественную оценку возможности реализации какого либо события, мы разлагаем все события, которые могут произойти на элементарные события (см. квант 1).

Например, если речь идет о вытаскивании карты из колоды, содержащей 36 карт, то под элементарными событиями понимается возможность извлечь шестерку пик, семерку пик и т.д. Общее количество элементарных событий в данном примере будет равно 36, ровно столько, сколько карт в колоде. В случае, когда мысленно проводятся механические испытания (вытаскивание карт из колоды, подбрасывание монеты и т.д.), естественно предположить, что все элементарные события равновозможны, т.е. нет преимуществ в реализации одних элементарных событий перед другими. Тогда количественной оценкой возможности реализации события А будет являться классическое определение вероятности данного события. Определяется эта вероятность как отношение числа элементарных событий, благоприятствующих наступлению события А к общему количеству элементарных событий:.

Пример 2.1В рассмотренном примере с картами если мы зададимся вопросом, какова вероятность, что вынутая из колоды наугад карта окажется достоинством не ниже десятки, то по данной формуле это легко вычислить.

Действительно, поскольку  (4 туза, 4 короля и т.д.), то .Пример 2.2Бросается игральная кость. Какова вероятность, что выпадет шестерка?Количество элементарных событий равно 6. Только одно из них благоприятствует наступлению события А. Следовательно, вероятность, что выпадет шестерка, равна .

Статистическое определение вероятности. Часто оказывается довольно сложно представить результат испытания в виде совокупности элементарных событий. Кроме того, не всегда элементарные события равновероятны. Например, когда студент идет на экзамен, четыре элементарных события — оценка 2, 3, 4, 5 — равновероятными не являются. В подобных случаях наряду с классическим используют статистическое определение вероятности. В качестве статистической вероятности события принимается относительная частота его реализации при большом числе испытаний. Если проводится n испытаний и при этом событие А реализовалось m раз, то относительная частота появления события А есть .Например, если монета подбрасывалась 2000 раз, и орел при этом выпал 982 раза, то статистическая вероятность события, что выпадет орел, равна относительной частоте его появления .

Геометрическая вероятность

В кванте 2 рассмотрены классическое и статистическое определения вероятностей. В частности, даже когда количество элементарных событий конечно, но нет никаких оснований считать их равновероятными, применяется понятие статистической вероятности.

Еще одним примером, когда понятие классической вероятности оказывается неприменимым, является ситуация, когда имеется неограниченное количество элементарных событий, которые нельзя даже пронумеровать. Например, если мы произвольным образом выбираем точку на заданном отрезке, то пространством элементарных событий будет множество всех точек, принадлежащих этому отрезку. В этом случае говорить о конечности множества элементарных событий не приходится. Вероятность выбора какой то конкретной точки, как и любой другой, равна нулю, но, в то же время, событие выбора этой точки не является невозможным, просто мы имеем дело с бесконечным числом элементарных событий, вероятность каждого из которых равна нулю. В том случае, если нет никаких оснований полагать, что одни точки обладают преимуществом выбора относительно других, имеет смысл говорить о вероятности того, что выбранная точка принадлежит некоторому подмножеству основного множества, из которого мы выбираем. Например, если мы выбираем точку на отрезке L= [0, 10], то имеет смысл ставить вопрос о вероятности, что выбранная точка окажется внутри отрезка l= [1, 2]. Если, как говорилось выше, преимуществ в выборе одних точек над другими нет, то естественно в качестве вероятности задать отношение меры множества l к мере множества L. В качестве меры выбирают геометрическую меру. Для одномерных объектов, таких, как отрезки, такой мерой является длина, для двумерных объектов — площадь, для трехмерных объектов — объем и т.д. Тогда вероятность, что наугад выбранная на отрезке [0, 10] точка окажется внутри отрезка [1, 2] будет равна 0,1.Пример 3.1Пол расчерчен квадратами со стороной а, как показано на рисунке:Подбрасывается монета радиуса r. Какова вероятность, что монета ляжет таким образом, что не будет пересекать ни одну из линий.

Решение. Нарисуем квадрат, внутрь которого попал центр монеты:Задача имеет смысл, если выполнено условие 2r < a. Отступим с каждой стороны квадрата внутрь на радиус монеты r и нарисуем меньший квадрат со стороной a - 2r. Если центр монеты попадает в маленький квадрат, то монета не пересечет ни одну из сторон большого квадрата. Если же центр монеты попадет за пределы маленького квадрата, монета обязательно пересечет хотя бы одну из сторон большого квадрата. Отсюда следует, что вероятность того, что монета не пересечет ни одну из линий, которыми расчерчен пол, есть отношение площади малого квадрата к площади большого квадрата: .

Пример 3.2Петя и Вася договорились встретиться между 15.00 и 16.00 часами дня возле библиотеки. Оба люди пунктуальные — если договорились, обязательно придут в произвольный момент указанного временного диапазона. Какова вероятность, что их встреча состоится, если каждый готов ждать другого не более 30 минут?

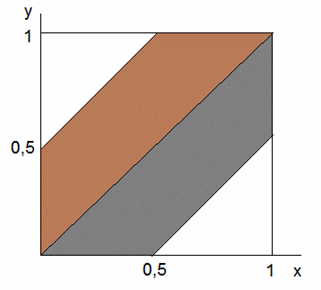
Решение. Обозначим за x время прихода Пети, за y — время прихода Васи и отложим на плоскости (x, y) время их прихода. Поскольку они люди пунктуальные, время их прихода представляет собой множество всех точек квадрата со стороной 1 (1 час). Рассмотрим 2 случая.

1. Петя приходит раньше. Можем написать 2 условия:, из которых первое означает, что Петя пришел раньше Васи, а второе, — что ждать он будет не более получаса. Множество точек внутри единичного квадрата, удовлетворяющее этим условиям есть верхняя заштрихованная трапеция.

2. Вася приходит раньше Пети. Также можем написать 2 услов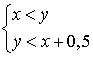ия:, из которых первое означает, что Петя пришел позже Васи, а второе, — что ждать Вася будет не более получаса. Множество точек внутри единичного квадрата, удовлетворяющее этим условиям, есть нижняя заштрихованная трапеция.

Вероятность встречи есть отношение площади двух заштрихованных трапеций к площади единичного квадрата. Площадь заштрихованной области есть площадь квадрата, равная 1, минус сумма площадей оставшихся треугольников. В результате получим: .

4.

Аксиомы теории вероятностей

В случае, когда пространство элементарных событий дискретно, можно сформулировать следующие аксиомы теории вероятностей.

1. Каждому событию A поставлено в соответствие некоторое число 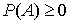, называемое вероятностью этого события.

2. Вероятность достоверного события равна единице: .

3. Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.

Следствия аксиом теории вероятностей

Следствие 1. В случае, если пространство элементарных событий состоит из равновозможных элементарных событий, то вероятность каждого из них .Убедимся в справедливости данного утверждения. Пусть все элементарные события равновозможны (равновероятны), а общее число элементарных событий равно . По второй аксиоме вероятность появления ходя бы одного из элементарных событий равна 1, или . Поскольку все элементарные события попарно несовместны, то из третьей аксиомы следует, что . Поскольку по условию элементарные события равновозможны, то , следовательно получаем, что , или .Равновероятные элементарные события, как правило, возникают при механических испытаниях (подбрасывание игральной кости, подбрасывание монеты, вытягивание карты из колоды).

Замечание. Формула  справедлива только в том случае, когда пространство элементарных событий конечно, а сами элементарные события равновероятны.Пример 4.1Подбрасывается игральная кость. Какова вероятность, что выпадет шестерка?Пространство элементарных событий состоит из 6 равновероятных событий (1, 2, 3, 4, 5, 6). Следовательно, .

Пример 4.2Подбрасываются 2 монеты. Какова вероятность, что на обеих выпадет орел?Пространство элементарных событий состоит из 4 равновероятных событий (орел — орел, орел — решка, решка — орел, решка — решка). Следовательно, . Следствие 2. В случае, если пространство элементарных событий состоит из Nравновозможных элементарных событий, то вероятность события A равна ,где  — количество элементарных событий, благоприятствующих наступлению события A.Пример 4.3Подбрасывается игральная кость. Какова вероятность, что выпадет число, меньшее 5?Пространство элементарных событий состоит из 6 равновероятных событий (1, 2, 3, 4, 5, 6). Нас устраивают 4 из них (1, 2, 3, 4). Следовательно, .

5.

Перестановки

При решении задач теории вероятностей часто приходится подсчитывать количество возможных вариантов событий. Действительно, формула, приведенная в кванте 4, —  — очень простая. Для вычисления вероятности наступления события A нужно всего лишь вычислить N — общее число элементарных событий и N_A — количество элементарных событий, благоприятствующих наступлению события A. В то же время не всегда простой оказывается задача вычисления величин N и N_A. Например, если необходимо вычислить вероятность того, что из вытянутых наугад восьми карт окажутся 3 шестерки, 2 туза, 1 король и ни одной десятки при условии, что изначально в колоде имеется 36 карт, то мы конечно можем воспользоваться формулой , но вот только подсчитать N и N_A

будет не совсем просто. Задачи, в которых вычисляется количество вариантов выбора решаются с помощью комбинаторики. Одним из понятий комбинаторики является понятие перестановки.

Перестановки — это комбинации, составленные из одних и тех же элементов и отличающиеся порядком их следования. Число всех возможных перестановок элементов обозначается P_n, и может быть вычислено по формуле:,где  — произведение всех натуральных чисел от 1 до n.

Действительно, будем расставлять n элементов по n местам в различном порядке. Заполнить первое место мы можем n способами. Когда первое место заполнено, перед нами n -1 — элемент для того, чтобы заполнить второе место. Таким образом, число способов заполнить второе место, когда первое заполнено выбранным ранее элементом, равно n -1. Причем такое число способов заполнить второе место есть для каждого варианта заполнения первого места, значит, число способов заполнить первые два места будет . Далее по аналогии, заполнить третье место можно n -2 способами, а первые три — n (n – 1) (n – 2) и т.д. Предпоследнее место можно заполнить двумя способами (осталось два элемента), последнее только одним. Число способов заполнить все n мест, а, значит, и число перестановок равно n!.

Пример 5.1Четверо участников квартета из басни Крылова всякий раз, пересаживаясь, исполняют десятиминутное произведение. Сколько времени потребуется на прослушивание всех вариантов исполнения?

Решение. Количество вариантов для пересаживания (перестановок) равно . Требуемое время для исполнения:24 × 10 мин. = 240 мин. = 4 часа.

6.

Размещения

В 5 кванте рассматривалось комбинаторное понятие «перестановка», когда происходит упорядочивание n различных элементов. Если из n различных элементов происходит выбор не всех, а только  различных элементов, то понятие перестановки применять нельзя. В этом случае мы имеем дело с размещениями.

Размещениями называют комбинации, составленные выбором из n различных элементов m различных элементов, отличающиеся либо составом элементов, либо порядком их следования. Число всех возможных размещений m элементов из n обозначается  и равно:(читается «а из эн по эм» или «а эм эн»). Действительно, будем расставлять n элементов по m местам в различном порядке. Заполнить первое место мы можем n способами. Когда первое место заполнено, перед нами n -1 элемент для того, чтобы заполнить второе место. Таким образом, число способов заполнить второе место, когда первое заполнено выбранным ранее элементом, равно n -1. Причем такое число способов заполнить второе место есть для каждого варианта заполнения первого места, значит, число способов заполнить первые два места будет n (n – 1). Далее по аналогии, заполнить третье место можно n -2 способами, а первые три — n (n – 1) (n – 2) и т.д. Предпоследнее место можно заполнить n –m + 2 способами (осталось n –m + 2 элементов), последнее — n –m + 1 способами.

Число способов заполнить все m мест, а, значит, и число размещений, равно:.

Замечание. Перестановка является частным случаем размещений. Действительно, в случае, когда , т.е. происходит выбор различных элементов из имеющихся элементов, очевидно, что понятия перестановки и размещения совпадают, а формула размещений в этом случае принимает вид:.Рассмотрим примеры применения формулы для размещений .Пример 6.1Имеется кодовый замок, чувствительный к порядку набора цифр. Код состоит из четырех различных цифр. Сколько всего различных кодов может быть набрано?Решение. В кодовом замке имеется всего 10 различных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Из них надо выбрать 4 различные цифры, при этом важен не только состав, но и порядок следования выбранных цифр. Очевидно, что мы имеем дело с размещениями, поэтому можем вычислить количество различных кодов по формуле:.

Сочетания

В 5 кванте и 6 кванте рассматривались комбинаторные понятия перестановка и размещение, когда происходит выбор m различных элементов из n различных элементов  при условии, что важен не только состав выбранных элементов, но и порядок их следования. В то же время, бывают ситуации, когда производится выбор различных элементов из различных элементов , и при этом важен только состав, а порядок следования не важен. В этом случае мы имеем дело с таким комбинаторным понятием, как сочетание.

Сочетаниями называются комбинации, составленные выбором m различных элементов из n различных элементов, отличающиеся только составом (но не порядком следования). Число всех возможных сочетаний m элементов из nравно:(читается «цэ из эн по эм» или «цэ эм эн»). Действительно, имеется  возможных размещений m элементов из n. Размещений, различающихся порядком следования элементов при заданном их составе, — m!, то есть на одно сочетание приходится m! размещений. Следовательно, количество сочетаний есть:.Рассмотрим примеры применения формулы для размещений.

Пример 7.1Имеется кодовый замок не чувствительный к порядку набора цифр. Код состоит из четырех различных цифр. Сколько всего различных кодов может быть набрано?Решение. Всего различных цифр 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Из них надо выбрать 4 различные цифры, при этом важен только состав, а порядок следования выбранных цифр роли не играет. Очевидно, что мы имеем дело с сочетаниями, поэтому можем вычислить количество различных кодов по формуле: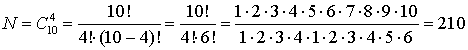.Пример 7.2В группе — 25 студентов. Наугад выбирают 4-х. Если они все вместе весят меньше 240 кг, всей группе ставится зачет по физкультуре, в противном случае вся группа бежит пятикилометровый кросс. Какое количество вариантов выбора есть у преподавателя физкультуры?Решение. Из 25 человек выбирается 4. При этом очевидно, что важен только состав, поскольку суммарный вес выбранных студентов не зависит от порядка их выбора. Следовательно, можно применить формулу для сочетаний:.

8.

Выбор с возвращением

В 5 кванте, 6 кванте и 7 кванте рассматривались комбинаторные понятия перестановка, размещение и сочетание, когда происходит выбор m различных элементов из n различных элементов . В то же время бывают ситуации, когда производится выбор m из nразличных элементов таким образом, что один и тот же элемент может быть выбран несколько раз. Например, из колоды карт вынимается одна карта, затем она возвращается обратно, колода перемешивается и процедура повторяется. В такой ситуации одна и та же карта может быть вынута из колоды несколько раз. В случае, когда выбор каждый раз осуществляется из одного и того же набора различных элементов, мы имеем дело с таким комбинаторным понятием, как выбор с возвращением.

Выбор с возвращением представляет собой комбинации m элементов из n элементов, отличающиеся составом или порядком следования, причем выбранный элемент возвращается на место и может участвовать в дальнейшем выборе. Число комбинаций mэлементов из n элементов, при условии, что выбранный элемент возвращается на место и может участвовать в дальнейшем выборе, равноn_m. Действительно, будем расставлять n элементов по m местам в различном порядке. Заполнить первое место мы можем n способами. Второе место можем заполнить тоже n способами. Причем такое число способов заполнить второе место есть для каждого варианта заполнения первого места, значит, число способов заполнить первые два места будет n₂. Заполнить третье и все последующие места мы можем также n способами. По аналогии существует всего n_mспособов заполнить m мест, выбирая из n элементов.

Замечание. В отличие от трех предыдущих комбинаторных понятий перестановки, размещения и сочетания, изложенных в 5 кванте, 6 кванте и 7 кванте, в которых обязательным условием было , для выбора с возвращением такого условия нет, поскольку выбранный элемент всякий раз возвращается обратно и участвует в дальнейшей процедуре выбора.Пример 8.1Монета подбрасывается 10 раз. Сколько существуют вариантов испытаний? То же самое рассмотреть для игральной кости.Решение.Каждое подбрасывание монеты есть выбор одного варианта из двух (орел, решка). Количество испытаний равно 10. По формуле выбора с возвращением получим:.Если 10 раз подбрасывается игральная кость, то n = 6, а m по-прежнему равно 10. Следовательно, .