Задача Коши и теорема Коши (формулировка) для диффе­ренциального уравнения первого порядка. Общее решение диф­ференциального уравнения первого порядка

Дифференциальное уравнение первого порядка связывает независимую переменную, искомую функцию и ее производные и в общем виде записывается следующим образом:

.

Разрешая это уравнение (если возможно) относительно y’ , получим

Полученное уравнение является частным случаем более общего дифференциального уравнения первого порядка

Общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную: .

Теорема Коши. Если функция f(х,y) и ее частная производная f'_y(х,y) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (x₀,y₀) области G, в некоторой окрестности этой точки существует единственное решение уравнения у'=f(x,у), удовлетворяющее условиям: у =у₀ при х =х₀

Теорема Коши дает возможность по виду дифференциального уравнения решать вопрос о существовании и единственности его решения.

Линейные дифференциальные уравнения первого порядка, Метод вариации произвольной постоянной. Уравнения Бернулли.

Линейным дифференциальным уравнением первого порядка на­зывается уравнение вида

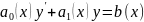где а₀(х), а₁(х) и b(х) — непрерывные функции (в некотором интервале).

Метод Бернулли. Ищем решение у = у(х) уравнения, делая замену . Подставляем функцию и ее произ­водную у'=и'v+uv’в уравнение и получаем:

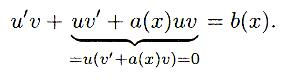
Группируем второе и третье слагаемые ("серединку").

Решаем 1ое уравнение системы( с разделяющимися переменными), находим , далее решаем 2ое (простейшее) – находим . Записываем ответ: у = и(х)v(х).

Дифференциальное уравнение вида называется уравнением Бернулли.

Однородные дифференциальные уравнения первого порядка.

Определение однородного дифференциального уравнения первого порядка связано с понятием однородной функции.

Функция f(х,у) называется однородной функцией степени k; если для любого λ имеет место тождество

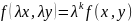
т. е. если при умножении x и у на одну и ту же постоянную λ функция умножается на .

Если k=0, т.е. , то функция называется просто однородной.

Простейший пример однородной функции — это однородный многочлен, т. е. многочлен все члены которого имеют одну и ту же степень k.

Однородное ДУ может быть представлено в виде:

Метод решения. Замена

Задача Коши и теорема Коши для дифференциального урав­нения порядка n (формулировка). Общее решение дифференци­ального уравнения.

Задачей Коши для дифференциального уравнения порядка n, разрешённого относительно старшей производной, называется задача отыскания решения этого уравнения, удовле­творяющего начальным условиям

, ,…

Теорема Коши. Если функция и её частные производные по переменным непрерывны в некоторой окрестности точки , то в

некоторой окрестности точки х₀ существует, и притом един­ственное, решение у = у(х) уравнения, удовлетворяющее начальным условиям.

Из теоремы Коши следует, что общее решение уравнения зависит от n произвольных постоянных

С₁., С₂, …С_n.

Для того чтобы решить задачу Коши, сначала на­ходят общее решение, а затем находят произвольные посто­янные из начальных условий,

т. е. С₁, C₂,….C_п находят из системы уравнений:

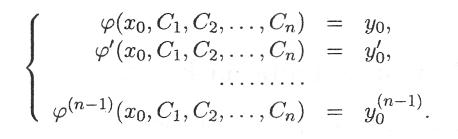
Простейшим дифференциальным уравнением порядка п называется уравнение вида

Дифференциальные уравнения, допускающие понижение порядка

(y⁽ⁿ⁾ =f(x), F(х ,у',у") = 0, F(у,у',у") = 0).

Д.У не завис. От у

Если k — наименьший порядок производной, входящей в урав­нение, то уравнение можно записать в виде

Делаем замену — новая неизвестная функция. Тогда , что понижает порядок

уравнения на k единиц:

Так как порядок уравнения стал меньше, то уравнение стало проще. Пусть z = z(х) — его общее решение. Тогда, чтобы ре­шить исходное уравнение, остается найти у из простейшего урав­нения у^(k) = z(х).

В случае уравнений второго порядка (n = 2)

замена у' = z сводит уравнение к уравнению первого по­рядка .

F(x, z, z') = 0.

Д.У не завис. От х

Такие уравнения второго порядка имеют вид (1)

Порядок уравнения понижается заменой обеих переменных: счи­таем у независимой переменной, а — некоторой неизвестной функцией от у. Тогда по правилу дифференциро­вания сложной функции имеем:

или, сокращенно,

Р = р(у):

Таким образом, замена , где р = р(у), (и тогда сводит уравнение (1) к уравнению первого поряд­ка (2)

Пусть р = р(у} — общее решение уравнения (2). Тогда, чтобы решить исходное уравнение, остается решить уравнение первого порядка с разделяющимися переменными у ‘= р(у).

Линейные дифференциальные уравнения (второго порядка). Линейность пространства решений однородного уравнения.

Линейным дифференциальным уравнением 2ого порядка называет­ся уравнение вида ₍₁₎

_{Уравнение (10)}

называется линейным однородным дифференциальным уравне­нием (сокращенно ЛОДУ) 2ого порядка, соответствующим уравнению (1). Ур авнение (1) при этом называют линейным неодно­родным дифференциальным уравнением (сокращенно ЛНДУ). Линейное уравнение (1о) называют также уравнением без пра­вой части, а уравнение (1) — с правой частью.

Решение уравнения (1) начинается с уравнения (1о).

Множество частных решений линейного однородного дифференциального уравнения образует линейное пространство.

Теорема о структуре общего решения однородного линейного дифференциального уравнения. неоднородного линей­ного дифференциального уравнения.

Фундаментальная система ре­шений.

Пусть имеется ЛНДУ порядка n

(1) где a_i(х) — непрерывные функции на отрезке [а; Ь], а

(1о) — ЛОДУ, соответствующее уравнению (1).

Теорема

1) Если есть решение ЛНДУ (1), есть решение ЛОДУ (1о), то сумма есть решение ЛНДУ.

2) Если есть какое-то одно решение ЛНДУ (1), то любое другое решение у — у(х) ЛНДУ (1) можно представить в виде

есть некоторое решение ЛОДУ (1о). Таким образом, общее решение ЛНДУ есть сумма частного (т.е. какого-то одного) решения ЛНДУ и общего решения соответ­ствующего ЛОДУ:

Если уравнение (1) есть, например, уравнение второго поряд­ка (n = 2), то общее решение ЛНДУ имеет вид

где — фундаментальная система решений соответствующего ЛОДУ. Таким образом, чтобы найти все решения ЛНДУ достаточно найти одно его решение и два решения соответствующего ЛОДУ.

Линейные однородные дифференциальные уравнения с по­стоянными коэффициентами. Вывод характеристического урав­нения. Общее решение в случае действительных различных кор­ней.

_{Пусть в уравнении}

коэффициенты a_i(х) = a_i = const: (1о)

Показательная функция у — е^λх является решением ЛОДУ (0о) тогда и только тогда, когда λ является корнем характеристи­ческого уравнения (2)

Характеристическое уравнение (2) получается из уравнения (1о), если производные у⁽ⁱ⁾ заменить на степени λⁱ переменной λ.

Если λ.₀ является корнем кратности k уравнения (2), то ему соответствует k решений

уравнения (1о). Если λ_1,2= α±β пара комплексно-сопряженных корней характеристического уравнения (2), то им соответству­ют два решения у1 — е^ах соsβх и у2 = е^ах sinβx уравнения (1о).

Пусть — характеристическое уравнение ЛОДУ второго порядка

Тогда два решения линейно независимы (образуют фундаментальную систему решений) и общее решение имеет вид

ЛОДУ с по­стоянными коэффициентами второго порядка. Фундаменталь­ная система решений в случае совпадающих действительных корней и в случае комплексных корней характеристического уравнения

Пусть — характеристическое уравнение ЛОДУ второго порядка

2. Корни уравнения действительные и равные

Тогда образуют фундаментальную систему решений, и общее решение имеет вид

3. Корни уравнения комплексные

Тогда функции

Образуют фундаментальную систему решений, и общее решение имеет вид

Неоднородные линейные дифференциальные уравнения с по­стоянными коэффициентами и специальной правой частью. Ме­тод неопределенных коэффициентов (формулировка).

ЛНДУ

(1)

с постоянными коэффициентами а_i, и специальной правой ча­стью f(x).

сначала нужно решить соответствую­щее ЛОДУ

(1о)

Затем нужно найти частное решение у* ЛНДУ. Это всегда мож­но сделать методом вариации произвольных постоянных. Тогда общее решение уравнения (1) имеет вид у = у* + уо, где уо — общее решение уравнения (1о).

Суть "метода неопределенных коэффициентов” состоит в том, что, если ЛНДУ имеет специальную правую часть, то у* можно найти в "таком же виде", как и правая часть уравнения. Зная вид у*, мы находим входящие в у* неизвестные (они же неопре­деленные коэффициенты), пользуясь тем, что у* должно быть решением дифференциального уравнения, т.е. при подстановке в уравнение должно получаться тождество.