
- •Что такое дифференциальное уравнение и его решение ? Примеры задач, приводящих к дифференциальным уравнениям (задача о радиоактивном распаде и задача о колебании груза напружине).
- •Линейные дифференциальные уравнения первого порядка, Метод вариации произвольной постоянной. Уравнения Бернулли.
- •Однородные дифференциальные уравнения первого порядка.
- •Задача Коши и теорема Коши для дифференциального уравнения порядка n (формулировка). Общее решение дифференциального уравнения.
- •Линейные дифференциальные уравнения (второго порядка). Линейность пространства решений однородного уравнения.
- •Теорема о связи первообразных одной и той же функции. Определение неопределенного интеграла.
- •Взаимная обратность операций интегрирования и дифференцирования. Свойство линейности неопределенного интеграла.
- •Задачи о вычислении площади криволинейной трапеции и нахождении длины пути по известной скорости.
- •Определение определенного интеграла. Теорема существования (формулировка). Геометрический и механический смысл интеграла.
Вычисление объемов с помощью определенного интеграла по известным площадям поперечных сечений.
Вычисление
объема тела по известным площадям
поперечных сечений. Пусть
тело Т
находится между двумя плоскостями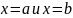 .
Тогда
его объем вычисляется по формуле
.
Тогда
его объем вычисляется по формуле
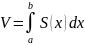
где
S(c)
— площадь сечения тела плоскостью х
= с,
перпендикулярной
оси Ох
и
проходящей через точку
 на этой оси.
В частности, отсюда получаются формулы
для объема тел вращения.
на этой оси.
В частности, отсюда получаются формулы
для объема тел вращения.
Объем
тела вращения.
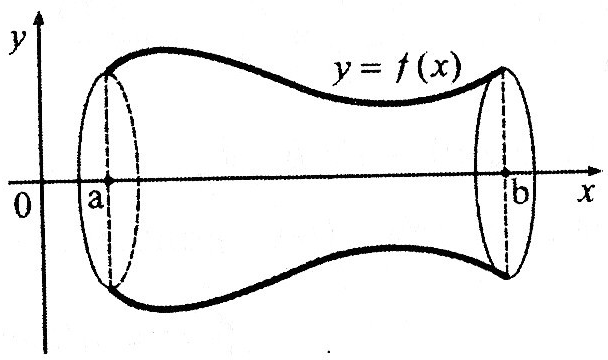
Объём
тела, полученного, при вращении
вокруг оси Ох
криволинейной
трапеции, ограниченной кривыми
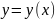 ,
,
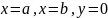 находятся
по формуле
находятся
по формуле
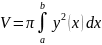
Несобственные интегралы с бесконечными пределами и от неограниченных функций. Определение и формула Ньютона-Лейбница. Исследование сходимости интегралов
Понятие
определенного интеграла
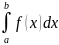 от ограниченной
функции
по конечному отрезку [a;b]
распространяют на случаи, когда
либо промежуток интегрирования является
бесконечным ("бесконечность
— сбоку"), либо функция является
неограниченной
("бесконечность — сверху").
Различают
несобственные интегралы первого и
второго родов. Общая конструкция
интеграла как предела интегральных
сумм в этих случаях
"не проходит". Из положения выходят
так: сначала бесконечность "отрубают",
а затем несобственные интегралы
определяют
как пределы определенных интегралов
в старом смысле (собственных
интегралов) с переменными пределами
интегрирования.
от ограниченной
функции
по конечному отрезку [a;b]
распространяют на случаи, когда
либо промежуток интегрирования является
бесконечным ("бесконечность
— сбоку"), либо функция является
неограниченной
("бесконечность — сверху").
Различают
несобственные интегралы первого и
второго родов. Общая конструкция
интеграла как предела интегральных
сумм в этих случаях
"не проходит". Из положения выходят
так: сначала бесконечность "отрубают",
а затем несобственные интегралы
определяют
как пределы определенных интегралов
в старом смысле (собственных
интегралов) с переменными пределами
интегрирования.
Пусть
функция
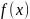 непрерывна
на полупрямой
непрерывна
на полупрямой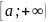 Несобственным
интегралом
Несобственным
интегралом
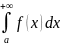 от функции
по
бесконечному
промежутку
,
или
несобственным
интегралом первого рода,
называется
предел
от функции
по
бесконечному
промежутку
,
или
несобственным
интегралом первого рода,
называется
предел
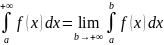
Если указанный предел существует и равен некоторому числу, то интеграл называется сходящимся, в противном случае — расходящимся.
Для несобственных интегралов сохраняется формула Ньютона-Лейбница
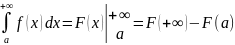
Что такое дифференциальное уравнение и его решение ? Примеры задач, приводящих к дифференциальным уравнениям (задача о радиоактивном распаде и задача о колебании груза напружине).
Обыкновенным
дифференциальным уравнением называется
соотношение
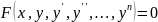 ,
связывающее
независимую переменную х,
функцию
у
— у(х) и
её
производные у', у",..., у(n).
Порядок n
старшей производной, входящей
в уравнение, называется порядком
дифференциального
уравнения.
,
связывающее
независимую переменную х,
функцию
у
— у(х) и
её
производные у', у",..., у(n).
Порядок n
старшей производной, входящей
в уравнение, называется порядком
дифференциального
уравнения.
Решением
дифференциального
уравнения называется
функция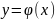 ,
при
подстановке которой в уравнение
получается тождество.
Решить
уравнение
—
это значит найти все его решения.
Решение уравнения часто получается в
виде функции, заданной
неявно уравнением Ф(х,у)
= 0.
Решения уравнения иногда
называют его интегралами.
,
при
подстановке которой в уравнение
получается тождество.
Решить
уравнение
—
это значит найти все его решения.
Решение уравнения часто получается в
виде функции, заданной
неявно уравнением Ф(х,у)
= 0.
Решения уравнения иногда
называют его интегралами.
