40. Частные производные и дифференциалы высших порядков функции нескольких переменных.

Частная производная

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции   определяется следующим образом:

Следует обратить внимание, что обозначение   следует понимать как цельный символ, в отличие от обычной производной функции одной переменной  , которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции:  , где   — частный дифференциал функции f по переменной x. Часто непонимание факта цельности символа   является причиной ошибок и недоразумений, как, например, сокращение   в выражении  . (подробнее см. Фихтенгольц, «Курс дифференциального и интегрального исчисления»).

Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции   в точке   по координате   равна производной   по направлению  , где единица стоит на  -ом месте.

Примеры:

Объём V конуса зависит от высоты h и радиуса r, согласно формуле

Частная производная объема V относительно радиуса r

которая показывает скорость, с которой изменяется объем конуса, если его радиус меняется, а его высота остается неизменной. Частная производная относительно h

которая показывает скорость, с которой изменяется объем конуса, если его высота меняется, а его радиус остается неизменным.

Полная производная V относительно r и h

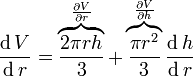
и

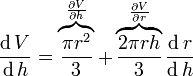
Различие между полной и частной производной — устранение косвенных зависимостей между переменными в последней.

Если (по некоторым причинам) пропорции конуса остаются неизменными, то высота и радиус находятся в фиксированном отношении k,

Это дает полную производную относительно r:

Уравнения, в которые входят частные производные, называются дифференциальными уравнениями в частных производных и широко известны в физике, инженерии и других науках и прикладных дисциплинах.

Дифференциалы высших порядков нескольких переменных:

Дифференциалом порядка n, где n > 1 от функции    в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть

  .

Дифференциал высшего порядка функции нескольких переменных

Если функция    имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .

Символически общий вид дифференциала n-го порядка от функции   выглядит следующим образом:

,где  , а    произвольные приращения независимых переменных  . Приращения    рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.

40. Понятие и необходимые условия локального экстремума функции нескольких переменных. Стационарные точки. Достаточные условия экстремума функции двух переменных. Нахождение наибольших и наименьших значений функции двух переменных в замкнутой области.

Локальный экстремум:

 Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Определение 7.4   Пусть функция   определена в некоторой окрестности  ,  , некоторой точки   своей области определения. Точка  называется точкой локального максимума, если в некоторой такой окрестности   выполняется неравенство   (  ), и точкой локального минимума, если    .     

Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум.

Локальный экстремум функции двух переменных       Необходимое условие локального экстремума дифференцируемой функции       Если   - точка экстремума функции f, то

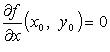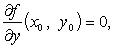 и   или 

     Достаточные условия локального экстремума дважды дифференцируемой функции 

     Обозначим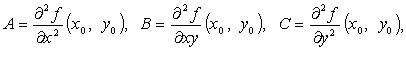   

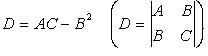
     Если D > 0, A > 0, то   - точка минимума.

     Если D > 0, A < 0, то   - точка максимума.

     Если D < 0, экстемума в точке   нет.

     Если D = 0, необходимы дополнительные исследования.

     Функции n переменных 

     Приращение функции в точке   

     Функция, дифференцируемая в точке   

 при 

 В этом случае дифференциал функции f в точке  :

 - частные производные первого порядка функции f.

Критической точкой дифференцируемой функции  , где   — область в  , называется точка, в которой все её частные производные обращаются в нуль. Это условие эквивалентно обращению в нуль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.