- •Классификация функций по свойствам.
- •Основные элементарные функции. Понятия сложной и обратной функций. Элементарные функции и их классификация.
- •Бесконечно малые и бесконечно большие функции, свойства. Связь бесконечно больших и бесконечно малых функций.
- •Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
- •Основные свойства пределов функции. Замечательные пределы.
- •Непрерывность функции в точке. Свойства функций, непрерывных в точке. Непрерывность основных элементарных функций.
- •Односторонняя непрерывность. Точки разрыва функции и их классификация.
- •Определение и свойства функции, непрерывной на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения. Теорема об обратной функции.
- •Понятие производной функции в точке. Геометрический и механический смысл производной.
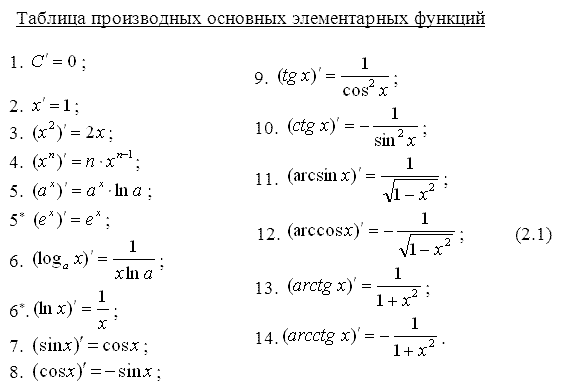
- •Правила вычисления производной, связанные с арифметическими действиями над функциями. Производные основных элементарных функций.
- •Производная сложной и обратной функций.
- •Производные функций, заданных в параметрическом виде и неявно.
- •Частные производные и дифференциалы высших порядков функции нескольких переменных.
- •Формальное определение
- •Понятия числового ряда, его суммы. Сходящиеся и расходящиеся числовые ряды. Необходимое условие сходимости числового ряда. Действия с числовыми рядами.
- •Знакопеременные числовые ряды. Понятия абсолютной и условной сходимости, их свойства.
- •Знакочередующиеся числовые ряды. Теорема Лейбница.
- •Числовые ряды с комплексными членами.
- •Функциональные ряды. Область сходимости функционального ряда. Равномерная сходимость функционального ряда. Признак Вейерштрасса.
- •Функциональный ряд
- •Сходимость
- •Свойства равномерно сходящихся функциональных рядов.
- •Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда, свойства степенных рядов.
- •Признаки сходимости
- •Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Формула Тейлора. Разложение основных элементарных функций в ряд Маклорена.
- •Формула Тейлора
- •Понятие тригонометрического ряда Фурье, условия его сходимости.
- •Основные элементарные функции комплексных переменных.
- •1. Дробно-рациональная функция
- •2. Показательная функция:
- •3. Тригонометрические функции:
- •4. Гиперболические функции:
- •5. Логарифмическая функция.
- •6. Общая степенная функция:
- •Дифференцируемость, условия Коши-Римана дифференцируемости функции комплексной переменной.
- •Определение аналитической функции комплексной переменной, свойства.
- •Интегрирование функций комплексной переменной. Дифференцирование Определение
- •Разложение аналитических функций в степенные ряды. Понятие ряда Лорана.
Понятие производной функции в точке. Геометрический и механический смысл производной.
Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференцированием.
Пусть
в некоторой окрестности точки
![]() определена функция
определена функция
![]()
Производная функции f в точке x0 называется предел, если он существует,
![]()
Производная функции y=f(x) в точке x0 обозначается символами
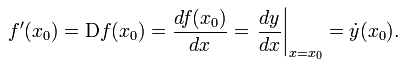
Г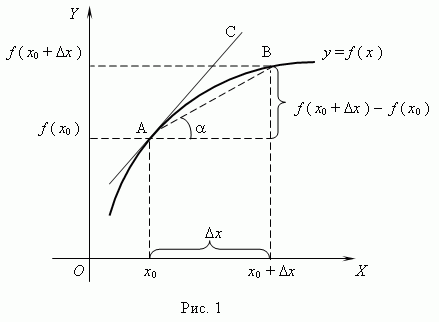 еометрический
смысл производной. Рассмотрим
график функции y = f ( x ):
еометрический
смысл производной. Рассмотрим
график функции y = f ( x ):
Из рис.1 видно, что для любых двух точек A и B графика функции:
![]()
где ![]() - угол
наклона секущей AB.
- угол
наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей. Если
зафиксировать точку A и двигать
по направлению к ней точку B,
то ![]() неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда
следует: производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке. В
этом и состоит геометрический
смысл производной.
неограниченно
уменьшается и приближается к 0, а секущая
АВ приближается к касательной АС.
Следовательно, предел разностного
отношения равен угловому коэффициенту
касательной в точке A. Отсюда
следует: производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке. В
этом и состоит геометрический
смысл производной.
Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x0 , f ( x0 ) ). В общем случае уравнение прямой с угловым коэффициентом f ’( x0 ) имеет вид:
y = f ’( x0 ) · x + b .
Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:
f ( x0 ) = f ’( x0 ) · x0 + b ,
отсюда, b = f ( x0 ) – f ’( x0 ) · x0 , и подставляя это выражение вместо b, мы получим уравнение касательной:
y = f ( x0 ) + f ’( x0 ) · ( x – x0 ) .
Механический
смысл производной. Рассмотрим
простейший случай: движение материальной
точки вдоль координатной оси, причём
закон движения задан: координата x
движущейся точки – известная
функция x ( t )
времени t.
В течение интервала времени от t0
до t0 + ![]() точка
перемещается на расстояние: x ( t0 +
) - x ( t0 )
=
,
а её средняя
скорость равна: va =
/
. При
точка
перемещается на расстояние: x ( t0 +
) - x ( t0 )
=
,
а её средняя
скорость равна: va =
/
. При
![]() 0
значение средней скорости стремится к
определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
0
значение средней скорости стремится к
определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
![]()
отсюда, v ( t0 ) = x’ ( t0 ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).
Правила вычисления производной, связанные с арифметическими действиями над функциями. Производные основных элементарных функций.
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
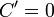
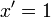
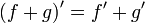
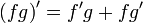
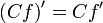
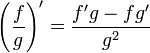 …(g ≠ 0)
…(g ≠ 0)