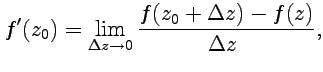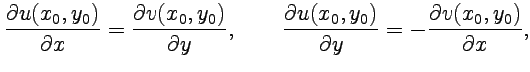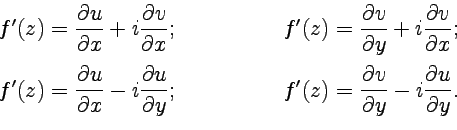- •Классификация функций по свойствам.
- •Основные элементарные функции. Понятия сложной и обратной функций. Элементарные функции и их классификация.
- •Бесконечно малые и бесконечно большие функции, свойства. Связь бесконечно больших и бесконечно малых функций.
- •Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
- •Основные свойства пределов функции. Замечательные пределы.
- •Непрерывность функции в точке. Свойства функций, непрерывных в точке. Непрерывность основных элементарных функций.
- •Односторонняя непрерывность. Точки разрыва функции и их классификация.
- •Определение и свойства функции, непрерывной на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения. Теорема об обратной функции.
- •Понятие производной функции в точке. Геометрический и механический смысл производной.
- •Правила вычисления производной, связанные с арифметическими действиями над функциями. Производные основных элементарных функций.
- •Производная сложной и обратной функций.
- •Производные функций, заданных в параметрическом виде и неявно.
- •Частные производные и дифференциалы высших порядков функции нескольких переменных.
- •Формальное определение
- •Понятия числового ряда, его суммы. Сходящиеся и расходящиеся числовые ряды. Необходимое условие сходимости числового ряда. Действия с числовыми рядами.
- •Знакопеременные числовые ряды. Понятия абсолютной и условной сходимости, их свойства.
- •Знакочередующиеся числовые ряды. Теорема Лейбница.
- •Числовые ряды с комплексными членами.
- •Функциональные ряды. Область сходимости функционального ряда. Равномерная сходимость функционального ряда. Признак Вейерштрасса.
- •Функциональный ряд
- •Сходимость
- •Свойства равномерно сходящихся функциональных рядов.
- •Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда, свойства степенных рядов.
- •Признаки сходимости
- •Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Формула Тейлора. Разложение основных элементарных функций в ряд Маклорена.
- •Формула Тейлора
- •Понятие тригонометрического ряда Фурье, условия его сходимости.
- •Основные элементарные функции комплексных переменных.
- •1. Дробно-рациональная функция
- •2. Показательная функция:
- •3. Тригонометрические функции:
- •4. Гиперболические функции:
- •5. Логарифмическая функция.
- •6. Общая степенная функция:
- •Дифференцируемость, условия Коши-Римана дифференцируемости функции комплексной переменной.
- •Определение аналитической функции комплексной переменной, свойства.
- •Интегрирование функций комплексной переменной. Дифференцирование Определение
- •Разложение аналитических функций в степенные ряды. Понятие ряда Лорана.
Основные элементарные функции комплексных переменных.
Следующие функции (как однозначные, так и многозначные) называют основными элементарными функциями:
1. Дробно-рациональная функция
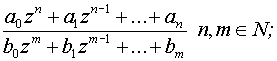
a) az+b,
(а![]() 0,
а, b
0,
а, b![]() C)
– линейная функция;
C)
– линейная функция;
б) zn , n N;– степенная функция с натуральным показателем;
в) 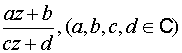 –
дробно-линейная функция;
–
дробно-линейная функция;
г) функция
Жуковского 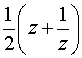 .
.
2. Показательная функция:
![]()
Наряду с введенным обозначением для показательной функции используют обозначение exp z.
Заметим, что на вещественной оси показательная функция комплексного переменного совпадает с показательной функцией действительного переменного. Непосредственная проверка убеждает, что на показательную функцию комплексного переменного переносится теорема сложения
![]()
Показательная функция комплексного переменного является периодической функцией с основным периодом 2i, т. е.
![]() .
.
3. Тригонометрические функции:
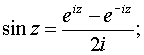
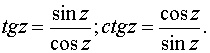
Для тригонометрических функций сохраняются теоремы сложения, а следовательно, и остальные формулы, справедливые для тригонометрических функций действительного переменного. Они являются периодическими функциями с теми же периодами, что и соответствующие тригонометрические функции действительного переменного.
Однако в случае комплексного переменного функции sinz, cosz ограниченными не являются.
4. Гиперболические функции:
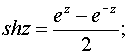
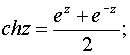
5. Логарифмическая функция.
Логарифмическая функция Lnz, при z определяется как обратная к показательной функции, причем
![]()
Так как показательная функция – периодическая с периодом 2i, то логарифмическая функция является многозначной. В каждой точке z она принимает бесконечно много значений.
Функция
![]()
где arg z – главное значение аргумента, называется главным значением логарифмической функции. Итак,
![]()
Известные правила о логарифме произведения и частного сохраняют свою силу и для многозначного логарифма, а именно: при z1 и z2, отличных от нуля, верны формулы
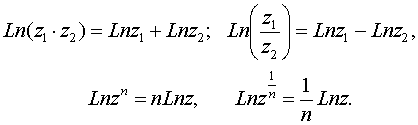
6. Общая степенная функция:
![]() , a
C.
, a
C.
Эта
функция многозначная, её главное значение
равно ![]() .
.
При a=1/n, n N получаем многозначную функцию – корень n-й степени из z:
![]()
7. Функции, обратные к тригонометрическим и гиперболическим, являются многозначными и выражаются через логарифмическую.
Поясним сказанное на примере функций а) w= аrcsin z, б) w= аrth z.
a) Имеем по определению
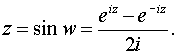
Откуда
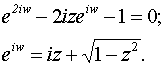
(Знаки ± в формуле решения квадратного уравнения можно опустить, если понимать корень как двузначную функцию).
Итак,
![]()
б) По определению w= аrthz z= thw. Откуда получаем
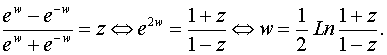
Таким
образом, 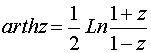 .
.
Для остальных обратных тригонометрических функций выполняются формулы:
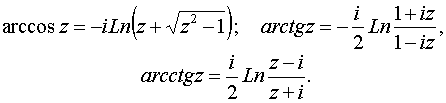
Дифференцируемость, условия Коши-Римана дифференцируемости функции комплексной переменной.
Условия
Коши — Римана,
называемые также условиями
д’Аламбера — Эйлера —
соотношения, связывающие вещественную ![]() и
мнимую
и
мнимую ![]() части
всякой дифференцируемой функции
комплексного переменного
части
всякой дифференцируемой функции
комплексного переменного ![]()
Производной функции ![]() в
точке
в
точке ![]() (обозначается
как
(обозначается
как ![]() или
или ![]() )
называется предел разностного отношения:
)
называется предел разностного отношения:
|
(20) |
если
он существует и не
зависит от
способа устремления ![]() к
нулю. Последнее требование явно указано
с целью еще раз подчеркнуть отличия по
отношению к функциям действительной
переменной, хотя, как правило, оно не
приводится, так как относится к определению
комплексного аналога предела. Требование
дифференцируемости
в
точке
накладывает
важные условия на свойства ее действительной
и мнимой частей и их производных, которые
должны подчиняться соотношениям:
к
нулю. Последнее требование явно указано
с целью еще раз подчеркнуть отличия по
отношению к функциям действительной
переменной, хотя, как правило, оно не
приводится, так как относится к определению
комплексного аналога предела. Требование
дифференцируемости
в
точке
накладывает
важные условия на свойства ее действительной
и мнимой частей и их производных, которые
должны подчиняться соотношениям:
|
(21) |
если ![]() и
и ![]() ,
которые называются условиями
Коши-Римана. На
основе (20)
и (21)
можно получить явные формулы
дифференцирования функций комплексной
переменной:
,
которые называются условиями
Коши-Римана. На
основе (20)
и (21)
можно получить явные формулы
дифференцирования функций комплексной
переменной:
|
(22) |
Пример
2-4. Найти
все точки, в которых дифференцируемы
функции ![]() :
:
1). ![]() 2).
2). ![]() 3).
3). ![]() .
.