40. Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Формула Тейлора. Разложение основных элементарных функций в ряд Маклорена.

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Определение

Пусть функция   бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд

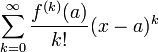
называется рядом Тейлора функции   в точке  .

Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.

Ряды Маклорена некоторых функций

Экспонента:

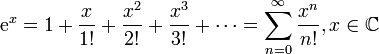
• Натуральный логарифм:

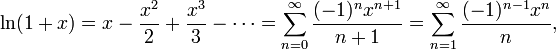 для всех 

• Квадратный корень:

 для всех 

 для всех 

• Конечный геометрический ряд:

 для всех 

• Тригонометрические функции:

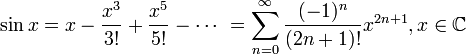
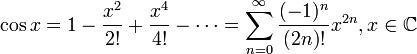
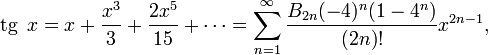 для всех   где   — Числа Бернулли

 для всех   где   — Числа Бернулли

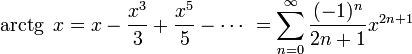 для всех 

 для всех 

Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

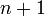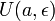
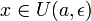
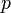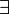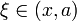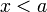Пусть функция   имеет   производную в некоторой окрестности точки  ,  Пусть  Пусть   — произвольное положительное число, тогда:   точка   при   ил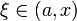и   при  :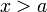

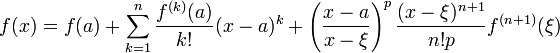
При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.

Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:

1)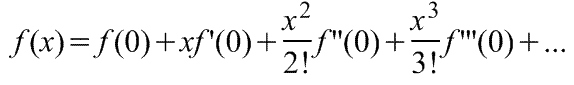  , где f(x) - функция, имеющая при а=0 производные всех порядков. R_n - остаточный член в ряде Маклорена (=Макларена) (Тейлора при а=0)определяется выражением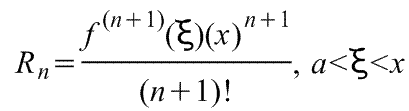 

2)

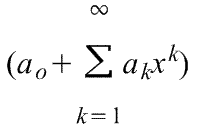
k-тый коэффициент (при х_k) ряда определяется формулой

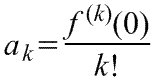
Разложение в ряд Маклорена

 1) Определяем производные иначе выражаясь,  , записываем ряд Маклорена для ,

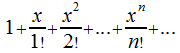
2) Находим интервал сходимости:

 

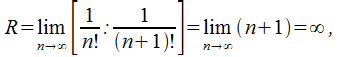
для ряда характерна абсолютная сходимость на промежутке .

3) Представим в форме Лагранжа (30.9):

(30.11)

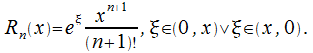
Функция монотонно возрастает, следовательно Учитывая то, что (30.10), в соответствии с признаком необходимости имеем

 

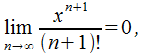
получается, что формула (30.11) является прооизведением ограниченной функции на б.м., следовательно .

40. Понятие тригонометрического ряда Фурье, условия его сходимости.

Тригонометрический ряд Фурье — представление произвольной функции   с периодом   в виде ряда

(1)

или используя комплексную запись, в виде ряда:

.

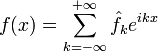Тригонометрическим рядом Фурье функции   называют функциональный ряд вида:

(1)

где

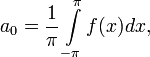
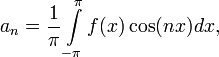
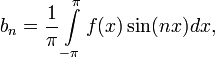
Числа  ,   и   ( ) называются коэффициентами Фурье функции  . Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию   в виде ряда (1), и нам надо определить неизвестные коэффициенты  ,   и  . Если умножить правую часть (1) на  и проинтегрировать по промежутку  , благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент  . Аналогично для 

Ряд (1) сходится к функции   в пространстве  . Иными словами, если обозначить через   частичные суммы ряда (1):

,

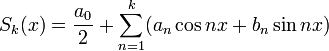то их среднеквадратичное отклонение от функции   будет стремиться к нулю:

.
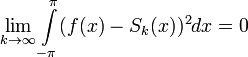