Свойства равномерно сходящихся функциональных рядов.
Свойства равномерно сходящихся последовательностей и рядов
Теоремы о непрерывности
Последовательность непрерывных в точке функций сходится к функции непрерывной в этой точке.
Последовательность 
функция
непрерывна
в точке
Тогда 
непрерывна
в
.
Ряд непрерывных в точке функций сходится к функции непрерывной в этой точке.
Ряд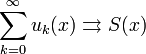 
функция непрерывна в точке
Тогда 
непрерывна
в
.
Теоремы об интегрировании
Теорема о переходе к пределу под знаком интеграла.
функция
непрерывна
на отрезке 
на
Тогда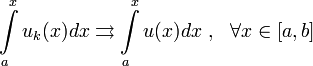 
Теорема о почленном интегрировании.
функция непрерывна на отрезке
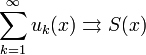на
Тогда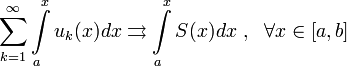 
Теоремы о дифференцировании
Теорема о дифференцировании под пределом.
функция непрерывно дифференцируема на отрезке
сходится
на
отрезке
Тогда 
—
непрерывно дифференцируема на
, 
на
Теорема о почленном дифференцировании.
функция непрерывно дифференцируема на отрезке
-
сходится
-
равномерно
сходится на отрезке
Тогда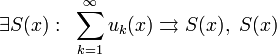 
—
непрерывно дифференцируема на
, 
на
Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда, свойства степенных рядов.
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
в
котором коэффициенты
берутся
из некоторого кольца 
.
Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
Первая теорема Абеля: Пусть ряд
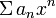сходится
в точке
.
Тогда этот ряд сходится абсолютно в
круге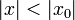 
и
равномерно по 
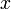на
любом компактном
подмножестве этого
круга.
Обращая
эту теорему, получаем, что если степенной
ряд расходится при 
,
он расходится при всех
,
таких что 
.
Из первой теоремы Абеля также следует,
что существует такой радиус
круга
(возможно,
нулевой или бесконечный), что при 
ряд
сходится абсолютно (и равномерно по
на
компактных подмножествах круга
),
а при 
—
расходится. Это значение
называется
радиусом сходимости ряда, а круг
—
кругом сходимости.
Вторая теорема Абеля: Пусть степенной ряд сходится в точке . Тогда он сходится равномерно по на отрезке, соединяющем точки 0 и .
Сумма степенного ряда как функция комплексного параметра является предметом изучения теории аналитических функций.
Свойства Степенных рядов:
Рассмотрим степенной ряд
с0 + с1 х + с2 х2 + ... + сn xn + ... , (10.1)
имеющий
радиус сходимости R>0 (R может равняться 
).
Тогда каждому значению х из интервала
сходимости соответствует некоторая
сумма ряда. Следовательно, сумма
степенного ряда есть функция от х на
интервале сходимости. Обозначим ее
через S(x). Тогда можно записать равенство
S(x) = c0 + c1 x + c2 x2 + ... + cn xn + ... , (10.2)
понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции S(x) в этой точке. В этом же смысле будем говорить, что ряд (10.1) сходится к функции S(x) на интервале сходимости. Вне интервала сходимости равенство (10.2) не имеет смысла.
Пример.
Найти сумму степенного ряда
1 - х + х2 - ... + (-1)n xn + ... .
Это
ряд, составленный из членов геометрической
прогрессии, у которой b1=1,
q= -x. Следовательно, его сумма есть
функция 
.
Ряд сходится, если |x|<1. Поэтому равенство
cправедливо
лишь для значений х 
(-1;
1), хотя функция
определена
для всех значений х, кроме х= -1.
Можно доказать, что сумма степенного ряда S(x) непрерывна и дифференцируема на любом отрезке [a, b] внутри интервала сходимости.
Равенство (10.2), справедливое в интервале сходимости степенного ряда, называют разложением S(x) в степенной ряд.
Для степенных рядов справедливы следующие утверждения:
Теорема 1.
Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны S`(x), S``(x), ... , S(n)(x).
Теорема 2.
Степенной
ряд можно неограниченное число раз
почленно интегрировать в пределах от
0 до х, если х
(-R;
R), причем получающиеся при этом степенные
ряды имеют тот же радиус сходимости,
что и исходный ряд, а суммы их соответственно
равны: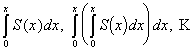 
.