4.Соотношение между сдвиговой и продольной вязкостями.

Для многих реальных материалов зависимость между и носит временной характер, т.е. определяется не только скоростью сдвига , но и продолжительностью деформации сдвига. В соответствии с тем, убывают или возрастают со временем напряжения сдвига , если материал деформируется с постоянной , различают две разновидности материалов: тиксотропные и антитиксотропные.

Реопексия сопровождается возрастанием в процессе деформирования с , также как и антитиксотропия. Однако реопексия обнаруживается только при малых и вызвана постепенным структурированием материала при механических воздействиях. При дальнейшем увеличении материал становится тиксотропным.

Полимеры в процессах переработки часто подвергаются деформации растяжения (формование заготовок для последующего раздува, вытяжка волокон и пленок и т.п.). Процесс растяжения жидкости описывается зависимостью, аналогичной закону Ньютона:

где - истинное напряжение в сечении, перпендикулярном к направлению растяжения;

- коэффициент продольной вязкости.

Для ньютоновских жидкостей, как показал Трутон, справедливо соотношение:

(4)

Для полимеров соотношение (4) удовлетворяется только при малых . В области высоких продольная вязкость возрастает значительно быстрее сдвиговой и соотношение достигает, например, для расплава ПС 350.

Лекция №2.

5.Вязкость полимеров. Температурная зависимость вязкости .

Вязкость – свойство оказывать сопротивление необратимому изменению формы образца. Большинство экспериментальных методов измерения сводится к независимому определению в опыте и и определение функции течения . Величина эффективной вязкости полимеров определяется как отношение величин , зависящее от значении или по результатам измерении на капиллярных или ротационных вискозиметрах. Размерность в системе СИ – , в системе СГС – пуаз (пз). .В полимергомологическом ряду вязкость может изменяться в очень широких пределах

Температурная зависимость вязкости существенно влияет на технологические свойства расплавов полимеров, определяет выбор режимов переработки, качество изделий и требования к контрольно-регулирующей аппаратуре. В настоящее время сложилось 2 подхода к рассмотрению . Они связаны с теориями абсолютных скоростей реакции и свободного объема в полимере.

Элементарный акт процесса течения состоит в преодолении молекулярно-кинетической единицей (МКЕ) потенциального барьера при переходе из одного положения в другое. Для этого она должна обладать достаточной энергией и, кроме того, вблизи исходного положения равновесия должно существовать свободное пространство – “дырка”, которой может отвечать новое равновесное положение МКЕ. Второе требование связано с условием одновременного изменения равновесных положений нескольких МКЕ. В таком случае течение становится кооперативным процессом. В теории Эйринга нахождение сводится к определению числа возможных переходов МКЕ через потенциальный барьер при различных температурах. Общие методы теории абсолютных скоростей приводят к следующему выражению вязкости жидкости:

, (5)

Поскольку мольный объем изменяется с температурой слабо, а величину энтропии принимают независящей от температуры, уравнение (5) можно переписать в виде:

, (6)

(формула Аррениуса-Френкеля-Эйринга: АФЭ),

где - энергия активации процесса;

- .

Поскольку , хотя и слабо, но все же зависит от , более точным для описания является выражение:

, (7)

Учет сомножителя дает незначительное уточнение по сравнению с экспоненциальным членом формулы (7).

А.И.Бачинский, используя другой подход, связанный с концепцией свободного объема, предложил формулу:

, (8)

(формула Бачинского)

согласно которой, текучесть прямо пропорциональна разности между удельным объемом жидкости и удельным объемом , занятым молекулами вещества, т.е. вязкость обратно пропорциональна свободному объему. Формула Бачинского качественно правильно описывает и имеет глубокий физический смысл, но для полимеров является лишь грубым приближением. Теория свободного объема в современном понимании основывается на наблюдениях А. Дулитла:

, (9)

Для явного введения температуры в формулу (9) можно использовать температурную зависимость свободного объема, предложенную М.Вильямсом, Р.Лэнделом и Дк.Ферри (ВЛФ):

, (10)

где - температура стеклования;

- свободный объем при ;

- коэффициент термического расширения свободного объема. Уравнение ВЛФ справедливо для . Допускается, что при свободный объем неизменен, что обусловлено замороженной конформацией полимерных цепей. Удельный объем жидкости изменяется с температурой линейно:

, (11)

где - удельный объем жидкости при ;

- коэффициент термического расширения жидкости. Подставляя (10) и (11) в (9) получаем:

, (12)

где - вязкость полимера при .

Объединяя входящие в (12) постоянные, получаем:

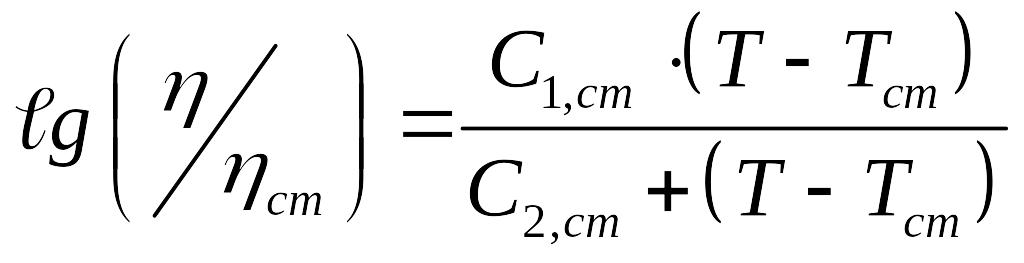, (13)

Формула (13) называется также формулой ВЛФ и применима от до .

В области близких к определяющее значение имеет свободный объем и его изменение, поэтому в этой области хорошо описывается формулой (13). При повышении важное значение приобретает скорость активации процессов, более точным для описания оказывается формула (6).

6. Энергия активации течения.

- это та энергия, которую сегмент должен получить в результате флуктуации тепловой энергии, для его отрыва от окружающих соседей, т.е. это энергия испарения вещества с молекулярной массой, равной молекулярной массе сегмента. Исходя из (8) определяется как угловой коэффициент прямой в координатах: - . В случае нелинейной зависимости - устанавливается зависимость от температуры так называемой “эффективной” (кажущейся) энергии активации. Для каждого заданного значения ее определяют как по тангенсу угла наклона касательной к кривой, выражающей зависимость в координатах - . Н.И.Шишкин показал, что во многих случаях величина линейно зависит от . Тогда функция имеет вид:

, (14)

где , , - эмпирические постоянные;

- размерный множитель, равный .

Таким образом, энергия активации является функцией температуры:

, (15)

Эта формула отражает тот факт, что с понижением температуры энергетические барьеры, которые преодолеваются в элементарном акте течения, повышаются. Это можно объяснить либо образованием новых межмолекулярных связей, либо увеличением числа связей, которые требуется преодолеть при элементарном акте течения. По смыслу теории Эйринга должно быть того же порядка, что и теплота испарения . Для многих низкомолекулярных соединений , однако при увеличении длины цепи начинает постепенно отставать от , стремясь к некоторому пределу. По мере удлинения молекулы размеры МКЕ становятся меньше полной длины макромолекулы: течение приобретает сегментный характер. С увеличением длины молекулы сегмент составляет все меньшую долю от ее размера.

Значение для полимеров относят к молю сегментов. Наименьшей отличаются полимеры с высокой гибкостью цепи и слабым межмолекулярным взаимодействием. Введение боковых заместителей в полимерную цепь увеличивает размеры сегмента и повышает . Таким образом, на величину оказывают влияние факторы, определяющие гибкость и взаимодействие макромолекул, прежде всего микроструктура цепи, содержание полярных групп, боковые ответвления. показывает, насколько сильно вязкость расплава полимера зависит от температуры. Чем больше , тем сильнее снижается с ростом . Поэтому ПП, например, снижается быстрее, чем ПЭНД с ростом . Но при любой скорости снижения с ростом , температура – мощное средство влияния на вязкость расплава. Даже у ПЭ расплава снижается почти в 10 раз при повышении на . Поэтому при переработке стремятся поднять насколько это возможно ( ).

определяется взаимодействием сегментов с окружением, поэтому энергия межмолекулярного и внутримолекулярного взаимодействия не зависит от числа сегментов в макромолекуле данного полимера, а следовательно и от его молекулярной массы. Поэтому в справочной литературе приводится независимо от молекулярной массы полимеров.

7.Зависимость вязкости от молекулярной массы и разветвленности полимеров. Критическая молекулярная масса. Если размеры сегмента меньше размеров макромолекулы, то элементарные акты течения не зависят от ММ. Однако для совершения необратимого перемещения макромолекулы в целом необходимо смещение центра тяжести всей макромолекулы. Но чем выше ММ полимера, т.е. чем больше сегментов в макромолекуле, тем большее число согласованных движений сегментов должно произойти для перемещения ее центра тяжести и тем более высокой должна быть вязкость.

Существует 2 области ММ линейных полимеров, разделенных характерным для каждого полимергомологического ряда критическим значением ММ . В обеих областях зависимость может быть представлена степенным законом:

, (16)

З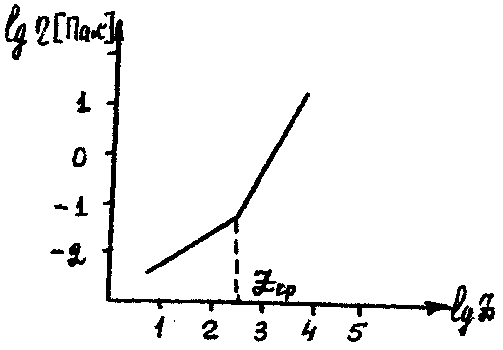 десь и - индивидуальные константы полимергомологического ряда. Величина , . Типичный пример таких экспериментальных данных – зависимость для полиметиленов.

Угловые коэффициенты участков ломанной линии (значения и ) до , после . - число атомов в цепи главных валентностей.

По достижении критической ММ изменяется комплекс свойств, присущих полимерам (вещество может быть отнесено к полимеру лишь по достижении ).

Достижение критической молекулярной массы принято связывать с появлением в полимере пространственной сетки узлов типа зацеплений макромолекул, которые характеризуются слабыми межмолекулярными взаимодействиями и соответственно низким потенциальным барьером. Это объясняет очень слабую зависимость от температуры. Аномалия вязкости проявляется при и может быть связана с уменьшением плотности сетки зацеплений под влиянием сдвиговой деформации. При с увеличением ММ и ростом и возрастает возможность разрушения сетки зацеплений – аномалия вязкости становится все более сильной. При у полимера обнаруживается способность переходить в высокоэластическое состояние, для которого типично существование 3-хмерной сетки.

Строение макромолекул существенно влияет как на , так и на степень аномалии вязкости. А.Чарлеби на примере полисилоксанов, подвергнутых -облучению, показал, что вязкость разветвленных полимеров меньше, чем вязкость линейных с той же ММ. Снижение вязкости с увеличением разветвленности описано также для ПС, ПЭ, полиэфиров. Влияние боковых ответвлений в макромолекулах на вязкость может быть столь значительным, что отношение при заданных и иногда достигает нескольких десятков. Хотя вязкость разветвленного ПС понижена по сравнению с линейным ПС, темп зависимости для образцов с постоянным числом боковых цепей, оказывается более высоким, чем для линейных (показатель степени в уравнении (16) равен 4,5). Влияние разветвленности на вязкость может быть понято, если учесть, как под влиянием разветвленности изменяется средний радиус инерции невозмущенного клубка макромолекулы. Это изменение выражается через конформационный параметр , равный отношению среднеквадратичных радиусов инерции. Для звездообразных полимеров, например:

, (17)

где - число ответвлений.

Замена величиной в формулах (16) дает возможность правильно описать разветвленных полимеров. Использование параметра приводит к тому, что независима от числа ответвлений. Снижение вязкости разветвленных полимеров по сравнению с линейными той же ММ наблюдается тогда, когда длина боковых ответвлений не превосходит некоторого критического предела. В зависимости от длины боковых ответвлений отношение изменяется от до .

С увеличением и влияние разветвленности макромолекул на полимера уменьшается и при высоких скоростях сдвига иногда может быть несущественным.

Лекция № 3.

Физические модели основных технологических процессов переработки полимеров: