31. Аналитические показатели динамического ряда, способы их расчета, взаимосвязь.

Для характеристики особенностей и закономерностей развития изучаемого явления во времени необходимо решить целый ряд задач и осветить широкий круг вопросов. К числу основных задач, возникающих при изучении динамических рядов, относятся: (1) характеристика интенсивности отдельных изменений в уровнях ряда с течением времени; (2) определение средних показателей динамики; (3) выявление закономерностей динамики ряда в целом; (4) интерполяция и экстраполяция; (5) выявление основных факторов, влияющих на изменение динамики исследуемого явления.

Динамический ряд - ряд последовательных уровней, сопоставляя которые между собой можно получать характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система абсолютных и относительных показателей динамики, к числу которых относятся: абсолютный прирост, коэффициент (темп) роста, темп прироста, абсолютное значение 1% и др. При этом, сравниваемый уровень называется текущим, а уровень, с которым производится сравнение - базисным. За базисный часто принимается либо начальный в динамическом ряду уровень, либо уровень, с которого начинается какой-то новый этап развития явления, отражаемого данным динамическим рядом.

Если производится сравнение каждого уровня ряда с предыдущим, то имеем цепные показатели динамики; при сравнении с базисным уровнем - базисные показатели динамики. В первом случае показатели динамики характеризуют интенсивность изменения уровней от периода (момента) к периоду (моменту), во втором - окончательный результат всех изменений в уровнях ряда за период от базового уровня до текущего. Выбор базиса должен быть обоснованным и отвечать сущности изучаемого явления.

Абсолютный прирост — это разность двух уровней ряда динамики. Он показывает, на сколько единиц данный уровень больше или меньше уровня, взятого для сравнения, и выражается в тех же единицах, что и уровни динамического ряда.

Цепной абсолютный прирост Δy_ц исчисляется как разность между сравниваемым (текущим) уровнем у_i и уровнем, который ему предшествует у_i-1:

Δy_ц = у_i - у_i-1

Базисный абсолютный прирост Δу_б исчисляется как разность между сравниваемым уровнем уi и уровнем, принятым за постоянную базу сравнения, y0:

Δу_б = у_i - y₀

Абсолютный прирост может быть положительной или отрицательной величиной, в последнем случае это снижение. Цепyой абсолютный прирост выражает абсолютную скорость роста.

Сумма цепных абсолютных приростов за какой-то период времени равна базисному абсолютному приросту за весь этот период. Разность между анализируемым и предыдущим базисными абсолютными приростами дает соответствующий цепной абсолютный прирост.

Темп роста — это отношение двух уровней ряда динамики. Он показывает, во сколько раз больше (или меньше) или сколько процентов данный уровень составляет по отношению к другому уровню, взятому для сравнения. В первом случае темп роста выражается в коэффициентах, во втором — в процентах.

Цепной темп роста Тц исчисляется как отношение между сравниваемым (текущим) уi и предшествующим ему уровнем У i-1: Тц= уi/ уi-1.

Базисный темп роста Тб исчисляется как отношение между сравниваемым уровнем уi и уровнем, принятым за постоянную базу сравнения у0, Тб = уi/ у0.

Если темп роста меньше единицы, то имеет место не рост, а снижение (падение) анализируемого уровня. Цепные темпы роста характеризуют относительную скорость (интенсивность) изменения уровней ряда динамики.

Последовательное произведение цепных темпов роста, выраженных в коэффициентах, за определенный период времени дает базисный темп роста за этот же период. Отношение анализируемого базисного темпа роста к предыдущему дает соответствующий цепной темп роста.

Темп прироста — это отношение абсолютного прироста к уровню, принятому за базу сравнения. Он обычно выражается в процентах и показывает, на сколько процентов уровень иного периода больше (или меньше) базисного.

Цепной темп прироста ΔТц исчисляется как отношение цепного абсолютного прироста ΔУц к предыдущему уровню Уi-1: ΔТц = (Уi - Уi-1)/ Уi-1=Тц-1 .

Базисный темп прироста ΔТб исчисляется как отношение базисного абсолютного прироста ΔУб к базисному уровню У0: ΔТб = (Уi - У0)/ У0=Тб-1 .

Темп прироста ΔТ вычисляется и как разность между темпом роста Т, выраженным в процентах, и 100%: ΔТ= Т-100%.

Темп прироста может быть как положительной, так и отрицательной величиной. В первом случае это свидетельствует о положительной динамике (росте), а во втором — об отрицательной динамике (снижении).

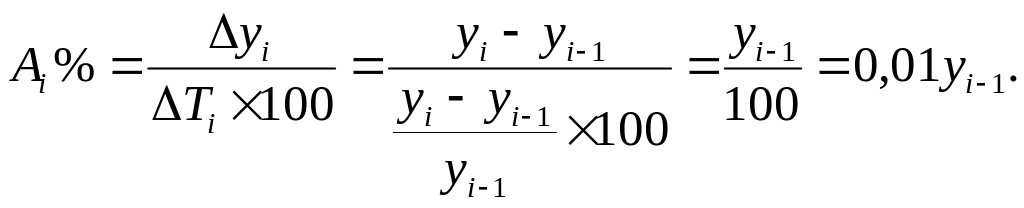А бсолютное значение одного процента прироста А_i% — это отношение абсолютного прироста ΔУ_i за определенный период (обычно за год) к темпу прироста ΔТ_i за этот же период, выраженному в процентах. Этот показатель раскрывает, какая абсолютная величина скрывается за относительной — одним процентом прироста.

Следовательно, количественно абсолютное значение одного процента прироста равно одной сотой части уровня, предшествующего анализируемому.

Если в исследуемый период наблюдалось снижение, а не рост явления, характеризуемого рядом динамики, то рассчитывается соответственно абсолютное значение одного процента не прироста, а снижения. Выражается абсолютное значение одного процента прироста (или снижения) в единицах измерения уровней анализируемого ряда динамики.