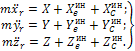11.Колебания материальной точки. Затухающие колебания точки. Вынужденные колебания.

Рассмотрим важный случай колебаний, возникающих, когда на точку, кроме восстанавливающей силы , действует еще периодически изменяющаяся со временем сила , проекция которой на ось Ох равна

. Эта сила называется возмущающей силой, а колебания, происходящие при действии такой силы, называются вынужденными. Величина Р является частотой возмущающей силы Возмущающей силой может быть сила, изменяющаяся со временем и по другому закону. Мы ограничимся рассмотрением случая, когда определяется указанным равенством. Такая возмущающая сила называется гармонической. Рассмотрим движение точки, на которую, кроме восстанавливающей силы , действует только возмущающая сила . Дифференциальное уравнение движения в этом случае . Разделим обе части этого уравнения на т и положим . Тогда, учитывая обозначение, приведем уравнение движения к виду . Уравнение является дифференциальным уравнением вынужденных колебаний точки при отсутствии сопротивления. Его решением, как известно из теории дифференциальных уравнений, будет , где -общее решение уравнения без правой части, а - какое-нибудь частное решение полного уравнения. Полагая, что p = k, будем искать решение в виде где А - постоянная величина, которую надо подобрать так, чтобы равенство обратилось в тождество. Подставляя значение и его второй производной в уравнение будем иметь: . Это равенство будет выполняться при любом t, если или . Таким образом, искомое частное решение будет . Так как , а общее решение имеет окончательно вид , где а и - постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от начальных условий) и частотой k, называемых собственными колебаниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колебаниями. Частота р вынужденных колебаний, как видно, равна частоте возмущающей силы. Амплитуду этих колебаний, если разделить числитель и знаменатель на , можно представить в виде: где , т. е. есть величина статического отклонения точки под действием силы . Как видим, A зависит от отношения частоты р возмущающей силы к частоте k собственных колебаний. Подбирая различные соотношения между р и k, можно получить вынужденные колебания с разными амплитудами. При амплитуда равна (или близка к этой величине). Если величина р близка к k, амплитуда A становится очень большой. Когда , амплитуда A становится очень малой (практически близка к нулю).Резонанс. В случае, когда , т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать .

12. Динамика относительного движения.

Движение точки относительно подвижной системы отсчета описывается дифференциальными уравнениями относительного движения.

Дифференциальное уравнение относительного движения точки:

(1)

где  переносная сила инерции (о силах инерции см. "Кинетостатика. Принцип Даламбера");   – кориолисова сила инерции.

Дифференциальные уравнения относительного движения точки в координатной форме:

(1a)

Из уравнений (1) и (1а) следует, что относительное движение точки можно изучать как движение относительно неподвижной системы отсчета, если к числу действующих на точку сил добавить переносную и кориолисову силу инерции.

В случае относительного покоя (v_r=0, ω_r=0) уравнение (1) приобретает вид:

т. е. приложенные к точке силы и переносная сила инерции образуют уравновешенную систему сил.

В случае движения относительно инерционной системы отсчета, т. е. системы отсчета, движущейся поступательно, прямолинейно и равномерно, уравнение (1) приобретает вид:

не отличающийся от   Таким образом, никакие наблюдения в инерциальной системе отсчета не позволяют установить факта ее равномерного прямолинейного движения (принцип относительности классической механики).