3. Пространства представления исследуемых процессов

Наряду с непосредственно зарегистрированными компонентами алфавита признаков в процедурах распознавания важную роль играют производные пространства представления сигналов, часто это спектральные, вейвлет преобразования, и другие существенно понижающие размерность пространства исходов и облегчающие расчеты разделяющих поверхностей.

В анализе оптических и ряда других волновых изображений получила представление объектов в «цветовых» пространствах. Одним из важных параметров регистрируемой компоненты оптического излучения является ее значение для фиксированной длины волны (частоты). Однако, объем информационного описания сигнала при этом существенно возрастает. Выход, который найден природой и его широко используют искусственные системы, заключается в формировании сигнала в определенном диапазоне длин волн. В оптике получившей название цвета. (Материал этого раздела достаточно обширен и в лекционном курсе задействован частично. Дополнительная информация представляет интерес для выполнения лабораторных работ).

 Для простоты вначале рассмотрим понятие цвета, сформулированное в среде специалистов в прошлые столетия и ориентированные на восприятие изображений человеком.

В системах, ориентированных на зрение человека, в результате цветовых измерений определяются три числа, цветовые координаты (ЦКС), полностью определяющие цвет при некоторых, строго стандартизованных условиях его рассматривания.

Основой математики описания цвета является положение о том, что любой цвет при соблюдении упомянутых условий можно представить в виде суммы трёх линейно независимых цветов. Групп линейно независимых цветов существует бесконечно много. Три выбранных линейно независимых цвета называют основными цветами. Они определяют цветовую координатную систему.

Экспериментальные результаты по цветовому восприятию получают при усреднении данных наблюдений большого числа наблюдателей; поэтому они не отражают точно свойств цветового зрения конкретного наблюдателя, а относятся к среднему стандартному наблюдателю.

Цвет геометрически представляется точкой в трёхмерном, цветовом пространстве или же вектором, начало которого совпадает с началом координат, а конец — с упомянутой точкой цвета. Точечная и векторная геометрическая трактовки цвета равноценны и обе используются в различных рассуждениях. Расширение толкования цвета как математического объекта приводит к понятию нереальных цветов, которые невозможно наблюдать или как-либо реализовать практически. Тем не менее, с этими цветами можно производить математические операции так же, как и с реальными цветами.

Своего рода «качество» цвета (цветность) удобно характеризовать в двумерном пространстве — на «единичной» плоскости. Например, проходящей через три единичные точки координатных осей. Линии пересечения единичной плоскости с координатными плоскостями образуют на ней цветовой треугольник, в вершинах которого находятся единичные значения. Если такой треугольник— равносторонний, его часто называют треугольником Максвелла. Другими словами, цветность определяется только направлением цветового вектора, а не его величиной и, следовательно, её можно охарактеризовать положением точки пересечения этого вектора с единичной плоскостью. Вместо треугольника Максвелла часто используют цветовой треугольник более удобной формы — прямоугольной и равнобедренный. Положение точки цветности в нём определяется двумя координатами цветности, каждая из которых равна частному от деления одной из цветовых координат на сумму всех трёх. Двух координат цветности достаточно, т. к., по определению, сумма её трёх координат цветности равна 1. Точка цветности опорного цвета, для которой три координаты равны между собой (каждая равна 1/3), находится в центре тяжести цветового треугольника.

Результаты сложения цветов можно считать линейными комбинациями чувствительности трёх типов приёмников человеческого глаза.

Основой всех ЦКС является система, кривые сложения которой были определены экспериментально описанным выше способом. Её основными цветами являются чистые спектральные цвета, соответствующие монохроматическим излучениям с дл. волн 700,0 (красный), 546,1 (зелёный) и 435,8 (синий) нм. Исходная (опорная) цветность — цветность равноэнергетического белого цвета Е (т. е. цвета излучения с равномерным распределением интенсивности по всему видимому спектру). Кривые сложения этой системы, приняты Международной комиссией по освещению (МКО) в 1931. Они известны под названием международной колориметрической системы МКО RGB (рис. 7.1). В этой системе координаты цвета монохроматических излучений (т. н. уд. координаты цвета показывают, какое количество единиц основных цветов воспроизводят при смешении воспринимаемого цвета монохроматического излучения данной длины волны мощностью в 1 Вт. Спектральные распределения значений уд. координат (по или ) наз. кривыми сложения Кривые сложения системы МКО RGB имеют отрицательные участки для некоторых цветов. Поэтому наряду с системой RGB МКО в 1931 приняла другую ЦКС, систему XYZ, в которой отсутствовали недостатки системы RGB.

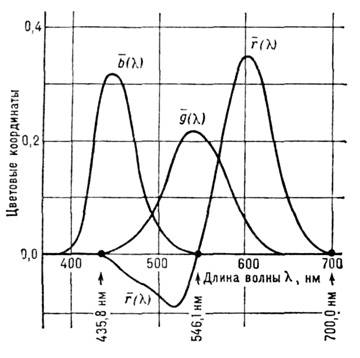
Рис 7.1. Кривые сложения для ЦКС МКО RGB.

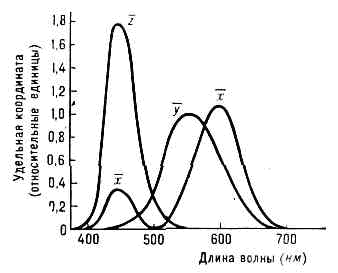
Рис.7.2. Кривые сложения для ЦКС МКО XYZ.

Оси системы XYZ — это нереальные цвета, выбранные так, что кривые сложения этой системы (рис. 7.2) не имеют отрицательных участков, а координата Y равна яркости наблюдаемого окрашенного объекта, т. к. кривая сложения у совпадает с функцией относительной спектральной световой эффективности стандартного наблюдателя МКО для дневного зрения.

На рис.7. 3 показан график цветностей (цветовой треугольник) х, у системы XYZ. На нём приведены линия спектр. цветностей, линия пурпурных цветностей, цветовой треугольник (R) (G) (В) системы МКО RGB, линия цветностей излучения абсолютно чёрного тела и точки цветностей стандартных источников освещения МКО A, В, С и D. Цветность равноэнергетического белого цвета Е (опорная цветность системы XYZ) находится в центре тяжести цветового треугольника этой системы. Система XYZ получила всеобщее распространение. Но она не отражает цветоразличительных свойств глаза. Одинаковым расстояниям на графике цветностей х, у в различных его частях не сопутствуют одинаковые зрительные различия между соответствующими цветами при одинаковой яркости. Предложено много эмпирических формул для подсчёта числа цветовых различий (порогов цветоразличения) между цветами. Более ограниченная задача — создание зрительного однородного графика цветностей — приблизительно решена. МКО на основании экспериментальных данных в 1960 рекомендовала такой график, полученный в 1937 Д. Л. Мак-Адамом путём видоизменения графика, предложенного Д. Б. Джаддом.

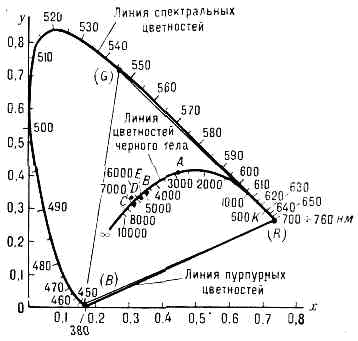
Рис.7.3. График цветностей х, у системы МКО XYZ и цветовой треугольник системы МКО RGB.

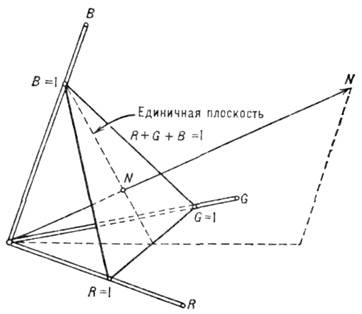
Рис.7.4. Единичная плоскость и нейтральный цвет N в цветовом пространстве RGB.

Приведённое описание показывает, что цель процесса измерения цвета — определение его в какой либо ЦКС. Чаще всего это —система МКО XYZ. Когда цвет представлен спектр. распределением излучения (испускаемого источником, либо отражённого или пропущенного предметом), то для нахождения его ЦК нужно использовать кривые сложения как взвешивающие функции, оценивающие это излучение.

Выражение цвета в определённой ЦКС (заданием его цветовых координат или же яркости и координат цветности) универсально и наиболее употребительно. Все вышесказанное иллюстрирует рис.7.4.

Расположение координатных осей цветового пространства тоже достаточно произвольно, но часто применяют такое расположение и масштаб, чтобы вектор белого цвета N пересекал бы единичную плоскость в центральной точке N треугольника, образованного вершинами единичных векторов R, G, В (рис. 7.4).

Любой цвет , точка цветности которого S (r, g, b )расположена внутри цветового треугольника, может быть получен как сумма положительных значений основных цветов системы RGB. Однако если цвет не входит в цветовой охват данной системы, то одна или две координаты цвета становятся отрицательными. Физически это означает, что измеряемый цвет не может быть получен смешиванием основных цветов, но измеряемый цвет в смеси с тем основным цветом, координата которого отрицательна, образует такой же цвет, как и смесь двух других основных цветов.

Рис.7. 5. Трёхкоординатное цветовое пространство, построенное на основных цветах (МКО, 1931) X, Y, Z.

Основные цвета X, Y, Z выбраны с таким расчётом, что кривая подобна кривой относительной спектральной эффективности (видности) глаза. Тогда координата непосредственно характеризует яркость цвета. В этой системе все реальные цвета укладываются внутри цветового треугольника (рис. 3.5).

Единичные цвета системы XYZ связаны с единичными цветами системы RGB след, преобразованиями:

Координаты цвета двух систем связаны между собой уравнением

Цветовое уравнение в системе XYZ записывается в виде

где -координаты цвета, а X, Y, Z- единичные векторы основных цветов. Координаты цветности в системе XYZ определяются аналогично их определению в системе RGB:

Излучение сложного спектрального состава состоит из суммы монохроматических излучений, поэтому все коэффициенты света сложного спектрального состава определяются как

Здесь - спектральное распределение энергии излучения, - удельные коэффициенты цвета монохроматических излучений, 683 - коэффициент перехода от энергетической величины лучистого потока (в Вт) к фотометрической величине светового потока (в люменах). Интервал суммирования обычно берётся 5 10 нм.

Рис. 7.6. Равноконтрастный цветовой график (МКО, 1960) с эллипсами ошибок, увеличенными по масштабу в 10 раз.

В литературе много описаны результаты представления цветности по окружности, например, понятие цветового круга, в котором инверсные цвета находятся друг против друга.

Сегодня понятие цвета шире и связано с селекцией наблюдаемого излучения в определенном достаточно локальном диапазоне длин волн или наборе поддиапазонов. Цветовая компонента может удерживать информацию о энергии излучения , где i – номер компонента (от 1 до N), – спектральная чувствительность i-го канала, - спектральная плотность потока от j – го объекта попавшая в i – канал, λ – длина волны оптического излучения, ... – рабочий диапазон длин волн.

При отказе от информации об общем уровне энергии переходят в пространство цветностей. Это понижает размерность исходного пространства на единицу и облегчает процедуру распознавания, если распознавание ведется и по цветовым признакам. Сформируем нормированные, не зависящие от общего уровня сигнала составляющие цветностей: .

Величина N определяет размерность цветового пространства до нормировки или после нормировки ( ). Часто говорят N – компонентном пространстве цветностей.

Размерность пространства цветностей на единицу меньше цветояркостного. Описание в цветностях теряет информацию об интенсивности оптического потока. Такое положение объясняет слабую зависимость выводов в системах распознавания от яркости осветителя.

И это только введение в науку о цвете. Многие годы ученые, художники постигали тонкости предмета, пытались предложить различные модели описания цветных изображений.

Очень распространена трехцветная модель RGB в видимом диапазоне длин волн оптического излучения. Она отображает чувствительность рецепторов глаза человека.

Для данного диапазона создана недорогая аппаратура считывания и генерации изображений, разработаны признанные типы описаний файлов и имеется множество графических программных продуктов для работы с ними. Как правило, информационное наполнение изображений полученных не в RGB пространстве переносят в него для более естественного анализа.

Человеческий глаз состоит примерно из 7 млн. колбочек и 120 млн. палочек. Функция палочек заключается в «ночном зрении» - светочувствительности и приспособлении к окружающей яркости. Функция колбочек - «дневное зрение» - восприятие цвета, формы и деталей предмета. В них заложены три типа воспринимающих элементов, каждое из которых воспринимает световое излучение только определенной длины волн, соответствующих одному из трех основных цветов: красному, зеленому и синему. Остальные цвета и оттенки получаются смешением этих трех.

Воспринимая цветовую информацию в диапазоне волн примерно от 380 нм (начало синих цветов) до 760 нм (конец красных цветов). Человеческий глаз имеет наилучшую чувствительность имеет в районе 550 нм (зона зеленых цвет).

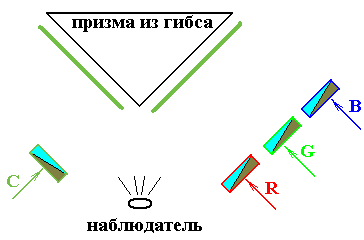
Рис.7.7. Схема опыта Грассмана

Много в цветовом представлении дали труды Ньютона, Ломоносова и многих других исследователей.

Немецкий математик Грассман в 1848 году на основе опытов конкретизировал следующие закономерности восприятия цвета человеком, которые могут, с определенными оговорками, расширены на любую перекрывающуюся трехцветную систему для глаза человека:

Четыре цвета всегда линейно зависимы, то есть , где . Для смеси двух цветов и имеет место равенство: .

Если цвет равен цвету и цвет тоже равен цвету , то цвет равен цвету независимо от структуры спектров энергии . Данная зависимость предполагает и наличие отрицательных сигналов среди слагаемых.

Цветовое пространство непрерывно. Если в смеси трех цветов один непрерывно изменяется, а другие остаются постоянными, то цвет смеси будет меняться непрерывно.

Как описано выше, распространенной рабочей цветовой моделью является модель RGB. Она идеально удобна для светящихся поверхностей (мониторы, телевизоры, цветные лампы и т.п.). Часто данную модель представляют в виде единичного куба с ортами: (1;0;0)- красный, (0;1;0)- зеленый, (0;0;1)- синий и началом (0;0;0)- черный.

Цвет в световом диапазоне длин волн достаточно долго является предметом изучения ученых, рабочим полигоном конструкторов, художников, дизайнеров, телевизионщиков и т.п. Такое положение отобразило и разнообразие используемых цветовых моделей.

Как признаки могут выступать цветовой тон - преобладающий основной цвет (длину волны, преобладающей в излучении); насыщенность цвета - чем она больше, тем «чище» цвет (то есть ближе к тоновой волне), например, у белого цвета – насыщенность = 0, так как невозможно выделить его цветовой тон. Введем, наконец, для завершения яркость (у черного цвета = 0, у белого=1).

Часто рассматривают два типа цветных объектов – самосветящиеся и излучающие объекты, такие как экраны кинескопов, плазменные панели, матрицы светодиодов и т.п. и несамосветящиеся объекты, отражающие или преломляющие падающий на них свет, такие как, например, оттиски на бумаге и т.п.

Для самосветящихся объектов используется аддитивное формирование оттенков, когда требуемый цвет формируется за счет смешения трех основных оттенков цветов. В этом случае удобно использование модели смешения RGB (Red, Green, Blue - красный, зеленый, синий).

Для несамосветящихся объектов используется субтрактивное формирование оттенков, основанное на вычитании из падающего света определенных длин волн. В этом случае удобно использование модели смешения CMY (Cyan, Magenta, Yellow - голубой, пурпурный, желтый).

Эти модели смешения показаны на рис. 7.8. На нем показаны результаты смешения цветов в аддитивной модели для трех самосветящихся площадок чистых цветов (красного, зеленого и синего) и результаты их смешения.

Цвета одной модели являются дополнительными к цветам другой модели. Дополнительный цвет - цвет, дополняющий данный до белого. Дополнительный для красного - голубой (зеленый + синий), дополнительный для зеленого - пурпурный (красный + синий), дополнительный для синего - желтый (красный + зеленый) и т.д.

Рис.7.8. Модели смешения цветов

Пример субтрактивного формирования оттенков показан на рис.7.9.

При освещении падающим белым светом в слое голубой краски из спектра белого цвета поглощается красная часть, затем из оставшегося света в слое пурпурной краски поглощается зеленая часть спектра, отраженный от поверхности бумаги свет еще раз подвергается поглощению и в результате мы видим синий цвет.

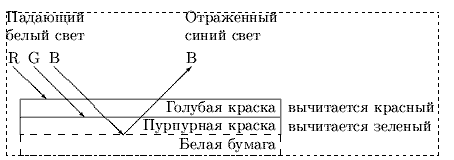
Рис.7.9. Цвет несамосветящегося объекта

Назначение цветовой модели - дать средства описания цвета в пределах некоторого цветового охвата, в том числе и для выполнения интерполяции цветов. Наиболее часто в компьютерной графике используются модели RGB (рис. 7.10), CMY, CMYK (Cyan Magenta Yellow Key, причем Key означает черный цвет), HSV , HSB, HLS и другие.

CMY (Cyan, Magenta, Yellow - голубой, пурпурный, желтый) - аппаратно-ориентированная модель, используемая в полиграфии для субтрактивного формирования оттенков, основанного на вычитании слоем краски части падающего светового потока. Цвета модели CMY являются дополнительными к цветам модели RGB, т.е. дополняющими их до белого. Таким образом, система координат CMY - тот же куб, что и для RGB, но с началом отсчета в точке с RGB координатами (1,1,1), соответствующей белому цвету. Цветовой куб модели CMY показан на рис. 7.11. Цвета, использующие белый свет, вычитая из него определенные участки спектра называются субтрактивными. Основные цвета этой модели: голубой (белый минус красный), фуксин (в некоторых книгах его называют пурпурным) (белый минус зеленый) и желтый (белый минус синий). Эти цвета являются полиграфической триадой и могут быть легко воспроизведены полиграфическими машинами. При смешение двух субтрактивных цветов результат затемняется (в модели RGB было наоборот). При нулевом значении всех компонент образуется белый цвет (белая бумага). Эта модель представляет отраженный цвет, и ее называют моделью субтрактивных основных цветов. Данная модель является основной для полиграфии и также является аппаратно-зависимой.

Рис. 7.10. Цветовой куб модели RGB

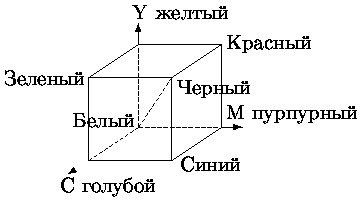
Рис. 7.11. Цветовой куб модели CMY

Преобразования между пространствами RGB и CMY определяются следующим образом:

[ R G B ]   =  [ 1 1 1 ]  -  [ C M Y ]

Причем единичный вектор-строка в модели RGB - представление белого цвета, а в модели CMY - черного.

Модель CMYK является дальнейшим улучшением модели CMY и уже четырехканальная. Поскольку реальные типографские краски имеют примеси, их цвет не совпадает в точности с теоретически рассчитанным (голубым, желтым и пурпурным). Особенно трудно получить из этих красок черный цвет. Поэтому в модели CMYK к триаде добавляют черный цвет. Почему-то в названии цветовой модели черный цвет зашифрован как K (от слова Key - ключ).Модель CMYK является «эмпирической», в отличие от теоретических моделей CMY и RGB. Модель является аппаратно-зависимой.

HSV (Hue, Saturation, Value - цветовой тон, насыщенность, количество света или светлота) - модель, ориентированная на человека и обеспечивающая возможность явного задания требуемого оттенка цвета (рис. 7.12). Подпространство, определяемое данной моделью - перевернутый шестигранный конус.

1. По вертикальной оси конуса задается V - светлота, меняющаяся от 0 до 1. Значению V = 0 соответствует вершина конуса, значению V = 1 - основание конуса; цвета при этом наиболее интенсивны.

2. Цветовой тон H задается углом, отсчитываемым вокруг вертикальной оси. В частности, 0° - красный, 60° - желтый, 120° - зеленый, 180° - голубой, 240° - синий, 300° - пурпурный, т.е. дополнительные цвета расположены друг против друга (отличаются на 180°).

3. Насыщенность S определяет насколько близок цвет к "чистому" пигменту и меняется от 0 на вертикальной оси V до 1 на боковых гранях шестигранного конуса.

Точка V = 0, в которой находится вершина конуса, соответствует черному цвету. Значение S при этом может быть любым в диапазоне 0-1. Точка с координатами V = 1, S = 0 - центр основания конуса соответствует белому цвету. Промежуточные значения координаты V при S=0, т.е. на оси конуса, соответствуют серым цветам. Если S = 0, то значение оттенка H считается неопределенным.

Рис. 7.12. Цветовая модель HSV

Модель HSB (Hue Saturation Brightness = Тон Насыщенность Яркость) построена на основе субъективного восприятия цвета человеком. Предложена в 1978 году. Эта модель тоже основана на цветах модели RGB, но любой цвет в ней определяется своим цветом (тоном), насыщенностью (то есть добавлением к нему белой краски) и яркостью ( то есть добавлением к нему черной краски). Фактически любой цвет получается из спектрального добавлением серой краски. Эта модель аппаратно-зависимая и не соответствует восприятию человеческого глаза, так как глаз воспринимает спектральные цвета как цвета с разной яркостью (синий кажется более темным, чем красный), а в модели HSB им всем приписывается яркость 100%. Модель является аппаратно-зависимой. H определяет частоту света и принимает значение от 0 до 360 градусов. V - значение (принимает значения от 0 до 1) или B - яркость, определяющая уровень белого света (принимает значения от 0 до 100%). Являются высотой конуса. S - определяет насыщенность цвета. Значение ее является радиусом конуса. Данная модель позволяет работать с 3 миллионами цветов.

Рис. 7.13. Цветовой круг при S=1 и V=1 (B=100%)

Модель HLS (Hue, Lightness, Saturation - цветовой тон, светлота, насыщенность) - ориентированна на человека и обеспечивающая возможность явного задания требуемого оттенка цвета (см. рис. 7.15). Эта модель образует подпространство, представляющее собой двойной конус, в котором черный цвет задается вершиной нижнего конуса и соответствует значению L = 0, белый цвет максимальной интенсивности задается вершиной верхнего конуса и соответствует значению L = 1. Максимально интенсивные цветовые тона соответствуют основанию конусов с L = 0.5, что не совсем удобно. Цветовой тон H, аналогично системе HSV, задается углом поворота. Насыщенность S меняется в пределах от 0 до 1 и задается расстоянием от вертикальной оси L до боковой поверхности конуса. Т.е. максимально насыщенные цветовые цвета располагаются при L=0.5, S=1.

В общем, систему HLS можно представить как полученную из HSV "вытягиванием" точки V=1, S=0, задающей белый цвет, вверх для образования верхнего конуса.

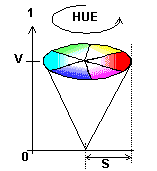
Рис. 7.14. Модели HSB и HSV

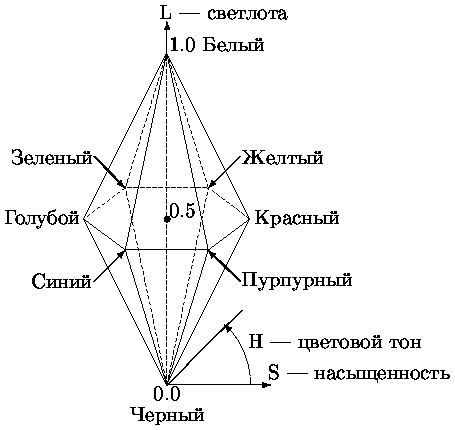
Рис. 7.15. Цветовая модель HLS

Цветовая модель Lab, использующаяся в компьютерной графике, является производной от цветовой модели XYZ. Компонент L несет информацию о яркостях изображения, а компоненты а и b - о его цветах (т. е. a и b - хроматические компоненты). Компонент а изменяется от зеленого до красного, а b - от синего до желтого. Яркость в этой модели отделена от цвета, что удобно для регулирования контраста, резкости и т.д.

Приведем формулы связи RGB и HSV:

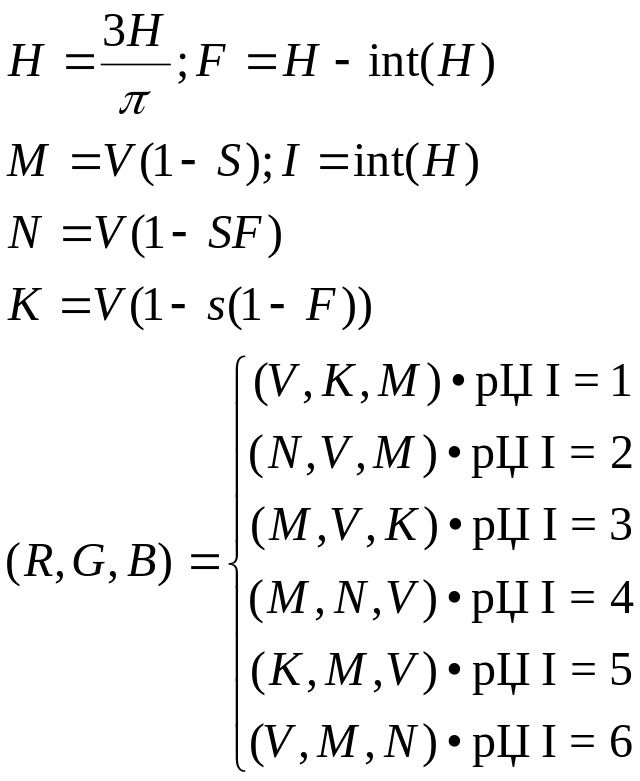
RGB в HSV:

RGB в HLS:

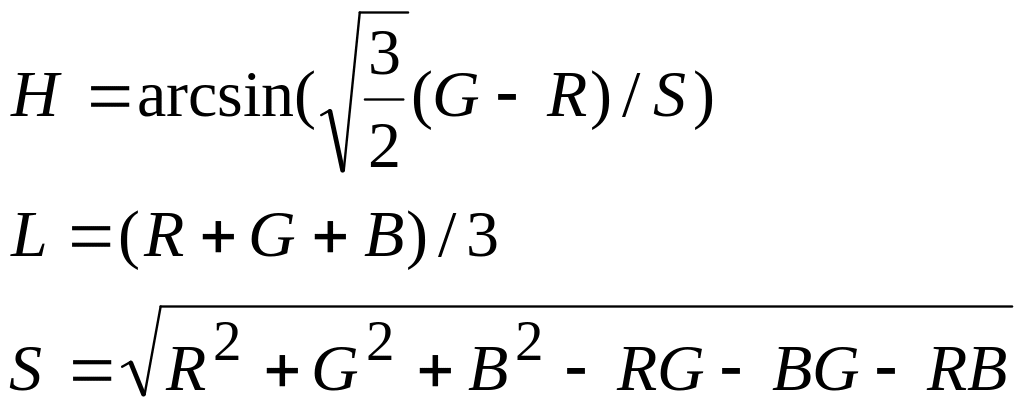
HLS в RGB:

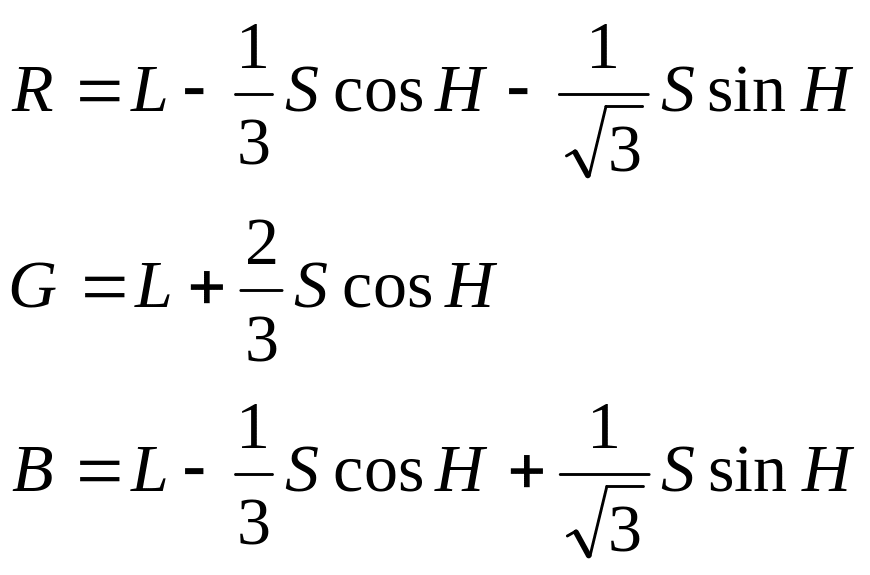
Пример перевода RGB в HSB. В данном формате RGB имеет на каждую из компонент R, G, B по 8 бит (256 уровней градации) - True Color. HSB представлен тремя плоскостями, соответствующими H, S, B, в виде черно/белых изображений с 256 уровнями градации .

Поскольку все цветовые модели описаны математически, они конвертируются одна в другую по простым формулам. Такие конверторы встроены во все графические программы.

При цветовых преобразованиях необходимо помнить, что между цветовыми моделями CMY, RGB, YIQ существуют аффинные преобразования, тогда, как между HLS и HSV- нет. Данное обстоятельство будет заметно, если изображение, содержащее непрерывные цветовые переходы, переводить, например, из HLS в RGB (на изображениях может появиться разрыв непрерывности).

Необходимо также показать и не менее чем RGB распространенную модель, используемую в телевидении, в которой формируются сигнал яркости Y и цветоразностные сигналы R-Y, B-Y.

, , , где a, c, d – соответственно для телевизионного сигнала равны 0,3; 0,59; 0,11 соответственно. Сигнал яркости передается в системах PAL, SECAM с шириной полосы 4 МГц, цветоразностные имеют ширину полосы 2 МГц и передаются попеременно. Таким образом, полоса сигнала яркости вдвое превышает полосу цветоразностных сигналов. Специализированные АЦП имеют соответственно частоты дискретизации от 13,5 Мотсчетов в секунду. Восстанавливая RGB специальные микросхемы видеоадаптторов, видеограберов увеличивают потоки до 27 Мотсчетов в секунду.