3. Описание объектов и классов в пространствах признаков. Алфавит признаков.

Эталоном системы распознавания образов до настоящего времени является система восприятия человека (если абстрагироваться от быстродействия).

Обычно целью создания систем распознавания является оптимизация ее функционирования над выборочным набором образов.

В общей схеме распознавания образов и принятия решений (рис. 5.1) преобладающей по трудовым затратам является операция преобразования пространства наблюдений с целью получения компактного описания объектов в пространстве признаков.

Системы распознавания объектов – сложные динамические системы с элементами искусственного интеллекта. Эти системы могут включать и подготовленных специалистов, экспертов т. е. и быть комплексными человеко-машинными системами. Сегодня они в основном специализированны.

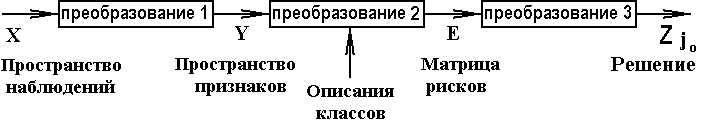
Рис.5.1. Обобщенная схема принятия решений при распознавании образов

В процессе разработки таких систем формируются описания физико-математических, химических, биологических, социальных моделей характеризующих объекты исследования.

В них должны отображаться только те признаки, значения которых можно измерить, или получить в процессе последующего исследования объекта распознавания.

Признаки могут быть детерминированные, вероятностные, логические и структурные.

Для формирования зон существования признаков, характеристики и параметры которых носят случайный характер, используют методы математической статистики.

Наиболее часто - это определение законов распределения и их параметров по имеющимся выборкам.

По результатам наблюдений проявлений признаков в различных реализациях распознаваемых объектов, ситуаций формируется статистическая гипотеза о виде и параметрах закона распределения.

Однако основную часть алфавита признаков, как правило, составляет множество детерминированных параметров и характеристик распознаваемых классов.

Классификация систем распознавания образов позволяет понять взаимосвязи в таких системах и решать задачу выбора признаков (процесс эвристический).

Классификация также способствует планированию использования как априорной информации (описание классов), так и апостериорных данных (измерения по данному неизвестному подлежащему классификации объекту).

Классификация - это распределение предметов, явлений по классам в зависимости от их общих свойств. В основе классификации лежат определенные принципы.

Для классификации систем распознавания можно использовать следующие признаки:

1. Однородность информации для описания распознаваемых объектов или явлений.

2. Способ получения апостериорной информации.

3. Количество и качество первоначальной априорной информации.

4. Характер информации о признаках распознавания.

1. Однородность информации. Под однородностью будем понимать - различную или единую физическую природу информации (признаков). По этому принципу системы распознавания (СР) образов делятся на простые и сложные. Простые системы распознавания характеризуются единой физической природой признаков. Например, только масса — для систем распознавания жетонов, монет в автоматах таких, как междугородный телефон, турникет метро; геометрические размеры - для таких систем распознавания, как всякого рода замки. Сложные системы распознавания характеризуются физической неоднородностью признаков.

2. Способ получения апостериорной информации. По этому принципу системы распознавания делятся на одноуровневые и многоуровневые. Многоуровневые сложные системы распознавания отличаются от одноуровневых тем, что не все признаки от разнородных физических измерителей используются непосредственно для решения задачи распознавания. Здесь на основе объединения признаков нескольких измерителей и соответствующей обработки могут быть получены вторичные признаки, которые могут как использоваться в следующей ступени, так и сами в свою очередь служить основой для объединения. То есть, получаем 2-й, 3-й и др. уровни признаков, определяющие иерархичность системы распознавания. Причем подсистемы, которые осуществляют объединение признаков, в свою очередь могут представлять собой также устройства распознавания (локальные системы распознавания). В одноуровневых СР информация о признаках распознаваемого объекта (апостериорная информация) формируется непосредственно на основе обработки прямых измерений;

В многоуровневых СР информация о признаках формируется на основе косвенных измерений, как результат функционирования вспомогательных распознающих устройств (например, при измерении дальности радиолокатором по временным задержкам излученного импульса, изменению его формы).

Таблица 5.1.

Системы распознавания по характеру информации	Характерные особенности
	метод решения задачи распознавания	метод априорного описания классов
Детерминированные	использование геометрических мер близости	координаты векторов-эталонов по каждому из классов или координаты всех объектов, принадлежащих классам
Вероятностные	вероятностный, основанный на вероятностной мере близости	вероятностные зависимости между признаками и классами
Логические	логический, основанный на дискретном анализе и исчислении высказываний	логические связи, выражаемые через систему булевых уравнений, где признаки - переменные, классы - неизвестные величины
Структурные	грамматический разбор предложения, описывающего объект на языке непроизводных структурных элементов с целью определения его правильности	подмножества предложений, описывающих объекты каждого класса
Комбинированные	специальные методы вычисления оценок	табличный, предполагающий использование таблиц, содержащих классифицированные объекты и их признаки (детерминированные, вероятностные, логические)

3. Количество и качество первоначальной априорной информации. Достаточно или недостаточно априорной информации для определения априорного алфавита классов, построения априорного словаря признаков и описания каждого класса на языке этих признаков в результате непосредственной обработки исходных данных. Соответственно этому системы распознавания делятся на системы без обучения, обучающиеся (ОСР) и самообучающиеся системы (ССР).

Многие системы распознавания однозначно нельзя разделить на указанные классы, так как каждая из локальных систем распознавания, входящих в их состав, сама может представлять как систему без обучения, так и систему обучающуюся или самообучающуюся. Для построения системы без обучения необходимо располагать полной первоначальной априорной информацией.

Для обучающихся систем нужно иметь дело с ситуацией, когда априорной информации не хватает для описания распознаваемых классов на языке признаков.

Исходная информация для обучающихся систем распознавания (ОСР) представляется в виде набора объектов , , , , где в первом приближении можно представить наличии трех видов слабо коррелированных между собой данных - детерминированных, случайных и лингвистических ( - числа осей пространства исходов по видам данных). Их распределение по m классам формирование и определение разделяющих функций является целью процесса обучения. Необходимо заметить то, что отнесение определенного сигнала сдатчика к определенной группе, например, не исключает его же отнесение и в группу . Данный сигнал, например, используется как детерминированный при различии объектов нескольких классов, и как случайный при работе с прочими классами.

Определение этой функции осуществляется путем многократного предъявления системе указанных объектов (из набора w1,w2,....,wl ) с указанием, какому классу они принадлежат.

То есть, на стадии формирования ОСР работают с “учителем”, осуществляющим указание о принадлежности предъявленного для обучения объекта. И прежде, чем система будет применяться, должен пройти этап обучения.

В отличии от систем без обучения и систем, обучающихся с учителем, для самообучающихся систем характерна недостаточность информации для формирования не только описаний классов, но даже алфавита классов. То есть, определен только словарь признаков распознавания.

Однако для организации процесса обучения задается некоторый набор правил, в соответствии с которым система сама вырабатывает классификацию.

Для ССР характерно наличие периода самообучения также как и для ОСР существует период обучения. ССР предъявляются объекты обучающей последовательности. Только при этом не указывается принадлежность их к каким-либо классам.

4. Характер информации о признаках распознавания. В соответствии с ее отличительными особенностями задач создания системы распознавания можно подразделить на детерминированные, вероятностные, логические, структурные (лингвистические), комбинированные. Характеристики систем по данному признаку классификации приведены в таблице 5.1.

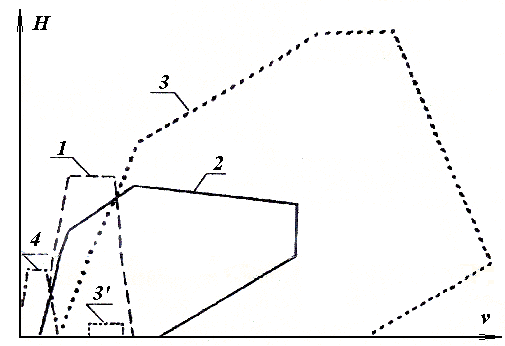
Рис.5.2. Классификация с двумя признаками и пятью классами.

Примером может служить и вариант распознавания воздушных целей по двум траекторным признакам (высотам и скоростям движения) (рис.5.2). Назначены классы: 1- самолеты больших размеров; 2- самолеты средних размеров; 3 – ракеты; - крылатые ракеты типа АЛКМ; 4 - вертолеты. Из рисунка видно то, что двух признаков не достаточно для распознавания объектов по назначенным классам. Дополнительно вводятся эффективные площади целей, поляризационные признаки, отражаемые в сигналах при узкополосном зондировании.

Приведенная схема односторонняя и лишь дополняет множество классификаций СР. Но она подчеркивает важность процедуры составления алфавита признаков и первичных преобразований выполняемых при этом. Признаки, как правило, выбираются итерационной процедурой, исходя из априорных сведений об объектах, фоне, и результатах сравнения перекрытий описаний классов. Сравнение проводится при отсутствии корреляции между признаками в их комплексном гиперпространстве.

Математические модели – цели первоначального (стартового) этапа составления алфавита признаков.

Впервые математические модели были использованы для решения практических задач в 30-х годах в Великобритании при создании системы противовоздушной обороны. Для разработки данной системы были привлечены ученые различных специальностей. Система создавалась в условиях неопределенности относительно возможных действий противника, поэтому исследования проводились на адекватных математических моделях. В последующие годы операционные исследования развиваются как наука, результаты которой применяются для выбора оптимальных решений при управлении реальными процессами и системами.

Хорошую модель составить не так просто. Математик Беллман Р. сказал «Если мы попытаемся включить в нашу модель слишком много черт действительности, то захлебнемся в сложных уравнениях; если слишком упростим ее, то она перестанет удовлетворять нашим требованиям». Для выполнения успешного моделирования надо удовлетворить трем правилам, которые применяются к задачам математического моделирования и формулируются следующим образом:

1. Необходимо учесть главные свойства моделируемого объекта;

2. Следует пренебречь его второстепенными свойствами;

3. Нужно уметь отделить главные свойства от второстепенных.

Математическая модель – это система математических соотношений приближенно в абстрактной форме, описывающих изучаемый процесс или систему, в нашем случае это оценка типа соотношений и вектора параметров, позволяющий отнести исследуемый объект к известному классу, или, хотя бы, облегчить классификацию.

Построение и расчет математической модели позволяют проанализировать ситуацию и выбрать оптимальные решения по управлению ей или обосновать предложенные решения. Применение математических моделей необходимо в тех случаях, когда проблема сложна и зависит от большого числа факторов, по-разному влияющих на ее решение.

Математические модели могут осуществлять предварительный выбор оптимальных вариантов решений по определенным критериям. Они научно обоснованы, и работник, принимающий решение, может руководствоваться ими при выборе окончательного решения. По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия. «Хорошая » модель. Должна быть:

1. целенаправленной;

2. надежной в смысле гарантии от абсурдных решений;

3. удобной в расчетах;

4. полной, с точки зрения возможностей решения поставленных задач;

5. адаптивной, т. е. позволяющей легко переходить к другим модификациям или обновлять данные;

6. допускающей постепенные изменения т.е. при последующих исследованиях становится все более точной.

По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.

В стохастических моделях неизвестные факторы – это случайные величины, для которых известны функции распределения и различные статистические характеристики. А в детерминированных моделях неизвестные факторы не учитываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи. По виду целевой функции и ограничений детерминированные модели делятся на: линейные, нелинейные, динамические и графические. В линейных моделях целевая функция и ограничения линейны по управляющим переменным. Построение и расчет линейных моделей являются наиболее перспективным разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения. Для линейных моделей любого вида и достаточно большой размерности известны стандартные методы решения. Нелинейные модели – это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) нелинейные по управляющим переменным. Графические данные обычно получают в результатах испытаний, они сложно объяснимы и часто плохо представляются известными уравнениями.

Построение моделей. При построении любой модели процесса управления желательно придерживаться следующего плана действий:

1. Сформулировать цели изучения системы;

2. Установить наиболее существенные для данной задачи факторы, компоненты и переменные;

3. Учесть тем или иным способом посторонние, не включенные в модель факторы;

4. Осуществить оценку результатов, проверку модели, оценку полноты мо-дели.

Виды моделей. Модели можно классифицировать как:

1. Функциональные модели – выражают прямые зависимости между эндогенными и экзогенными переменными;

2. Модели, выраженные с помощью систем уравнений относительно эндогенных величин;

3. Модели оптимизационного типа. Основная часть модели – система уравнений полученных относительно эндогенных переменных. Цель – найти оптимальное решение для некоторого показателя;

4. Имитационные модели – весьма точное отображение процесса или явления. Математические уравнения при этом могут содержать сложные, нелинейные, стохастические зависимости.

Имитационные системы занимают в моделировании особое место. В принципе, любая модель имитационная, ибо она имитирует реальность. Имитационная система – это совокупность моделей, имитирующих протекание изучаемого процесса, объединенная с информационной базой и специальной системой вспомогательных программ, позволяющих достаточно просто и оперативно реализовать вариантные расчеты. Таким образом, под имитацией в тренажерах понимают результаты расчетов адекватные параметрам имитируемым объектам.

Решение задач для многомерных систем сопряжено с большими трудностями, которые носят как математический, так и эксплуатационный характер, ибо часто требует затрат неприемлемых объемов машинного времени. Подходы к проблеме снижения порядка сложности моделей могут быть разные. Разумеется, сложная нелинейная система может быть эквивалентна линейной системе в определенных условиях. Существенные свойства управляемых систем, такие, как управляемость, устойчивость, оптимальность решений, сохраняются при переходе к эквивалентной системе.

Методология моделирования. Моделирование процессов управления предполагает последовательное осуществление трех этапов исследования:

Первый этап – от исходной практической проблемы до теоретической чисто математической задачи;

Второй этап – математическое изучение и решение этой задачи;

Третий этап – переход от математических выводов обратно.

Математическая модель связана с функционированием объекта и ориентирована на решение поставленной задачи. Технологическим объектам, например, свойственна целенаправленность. Это обстоятельство требует, при моделировании технологического объекта, обратить самое пристальное внимание на цели и задачи, которые должен решать данный технологический объект.

Построение комплексных математических моделей, описывающих процессы распознавания, реально возможно только в рамках теории сложных систем. Наиболее подходящим аппаратом описания процессов и выходных сигналов, сообщений, в данном случае, является математическая теория систем и особенно аппарат математических структур.

Математическая теория систем предполагает наличие, прежде всего общей цели в функционировании компонентов системы. Система считается заданной, если имеется ее модель. Исходно, не редко, это конструкторская документация, математические, физические модели, описывающие сигналы в компонентах системы. Математическая модель такой системы сегодня представляется набором связанных основных множеств. Связующим звеном между составными частями системы будем считать сигналы, несущие информацию об распознаваемых образах или ситуациях.

Часто математическая структура представляется набором объектов различной природы

,

где - элементы структуры, в том числе и виртуальные, в общем случае с неизвестными фрагментами описаний (сигналы, компоненты и т.п.).

Отношение – термин обозначающий пространство, в котором существуют всех комбинаций элементов, их взаимное расположение и взаимосвязи. В радиофизике часто сигналы заданы в узлах пространственной решетки, это упрощает, структурирует анализ.

Такие фразы при описании отношений, как - произвольное подмножество всех кортежей элементов традиционны. На теоретико-множественном языке понятие отношений связей между объектами. Например, - описание структуры набора №12 (кортежа) в пятимерном пространстве параметров (например, 3D координат, длины волны излучения и времени). Множество элементов, входящих хотя бы в один кортеж называют полем этого отношения.

Отображение - закон, график, нечеткая зависимость, показывающая связь сигналов на входе и выходе элемента или их набора.

Описанный подход позволяет работать с известными закономерностями, чертежами, графиками, нечеткой информацией в рамках одной системы, дополняя и уточняя ее во времени существования.

Описание систем ведется в рамках внешних (пример черного ящика) и внутренних моделей различного уровня и глубины представления. В ходу структурные, функциональные, принципиальные схемы. Для сигналов широко используют независимость реакции элементов системы от наличия других сигналов, величин сигналов. То есть начальный этап анализа это линейные, изопланарные, дифракционно-ограниченные реакции элементов системы на входные сигналы. Безаберрационная оптическая система изображает светящуюся точку в монохроматическом свете в виде дифракционной фигуры, состоящей из центрального яркого пятна (кружка Эри), и ряда светлых концентрических колец, разделенных темными промежутками, в которых освещенность падает до нуля.

В этих ограничениях реакцию объектива системы можно выразить, как сумму сверток от взвешенных входных (как правило, элементарных - ) сигналов с функцией рассеивания точки объектива.

, где - коэффициент увеличения, - коэффициент пропускания объектива, - входные сигналы, часто заданные в узлах квадратной решетки, - функция рассеивания точки, характеризующая объектив.

Выражение для аберраций может также упрощено

Эквивалентный радиус сферической аберрации , комы , астигматизма , увеличивающие размер кружка Эри, можно получить из выражений:

, , , где , , - соответствующие коэффициенты, характеризующие качество оптической системы и юстировки - угловое поле в пространстве предметов.

Все модели дополняют друг друга на различных этапах анализа и синтеза оптико-элекронных систем.

Переход от элементов одной природы к элементам другой осуществляется через соответствующие отношения. Например, пространственные частоты в изображении на CCD – матрице переходят во временные частоты электрических сигналов , где - длина строки сканирования, - интервал времени сканирования строки (не учитывает синхросигнал), , - пространственная и временная частоты на объекте в плоскости предметов и в сигнале. Оптическая передаточная функция где - передаточные функции составляющих аберрации вдоль осей , , , .

Для полноты картины добавим «аберрацию», обусловленную смазом изображения при регистрации кадра матричным фотоприемником. , где - скорость движения вращающегося изображения, - время интегрирования заряда в одном кадре, - число накапливаемых кадров (в условиях слабого освещения используют суммирование подряд идущих кадров без смещения), - пространственная частота в направлении смещения.

Считается аксиомой то, что с увеличением числа признаков вероятность правильного распознавания неизвестных объектов также увеличивается.

Обычно стремятся назначить независимые между собой признаки распознавания.

Снижение эффективности распознавания за счет увеличения числа классов может быть скомпенсировано увеличением размерности вектора признаков. Компромисс между размерами алфавита классов и объемом рабочего словаря признаков обеспечивает решение задачи оптимальным образом. Для обеспечения этого компромисса требуется предварительная формализация задачи. Формализация исходных данных, оптимизация алфавита классов и словаря признаков в условиях ограничений V ={v1 ,v2 ,...,vn }, компоненты которого vj равны 1, если данный признак априорного словаря используется в рабочем и 0 в противном случае. Этот вектор носит название вектора отбора.