
- •Курс лекций
- •«Теория распознавания»
- •Введение
- •История развития теории распознавания, основные понятия, содержимое литературных источников
- •Математические истоки тр. Случайные события, процессы, смеси, свойства оценок.
- •Специфика оценок в математике распознавания.
- •Риск и его оценка. Модели полезности. Описание последствий ложного распознавания.
- •Описание объектов и классов в пространствах признаков. Алфавит признаков.
- •Анализ метрики пространства признаков. Минимизация объема описаний. Решающие границы в пространстве признаков.
- •Пространства представления исследуемых процессов
- •Сделаем вставку с примерами использования математических приемов снижения объемов описания изображений.
- •Логические методы распознавания, их специфика и применение.
- •Структурные методы распознавания, их специфика и применение.
- •Корреляционные методы и алгоритмы распознавания.
- •Проделав выше указанные операции получим оптимальное значение коэффициента суммирования
- •Сложные образы в задачах распознавания.
- •Обратные задачи в распознавании, тренажеры, ложные объекты.
- •Имитация поведения объектов в тренажерах, виртуальных моделях.
- •Более детально рассмотрим снижение порядка сложности моделей пространства состояний для линейных непрерывных стационарных систем:
- •Расчет эффективности распознавания.
- •Перспективы задач распознавания в обработке сигналов, компьютерных технологиях.
- •Список рекомендуемой литературы
- •Содержание
- •Учебное пособие для студентов факультета радиофизики и компьютерных технологий
Структурные методы распознавания, их специфика и применение.
Распознавание
объектов по типу индикатрисы отражения
поверхности. Способность
поверхности объектов по различному
рассеивать падающее излучение так же
в виде набора признаков может входить
в алфавит признаков. Яркость поверхности
зависит от направлении, под которым она
наблюдается, и от направления падающих
лучей. Можно описать эти зависимости в
локальной системе координат на поверхности
объекта (рис. 9.1).Рассмотрим нормаль n к
поверхности и произвольную линию на
ней. Н
аправления
можно описать с помощью углов
![]() между лучом и нормалью и
между лучом и нормалью и
![]() между ортогональной проекцией луча
на поверхность и линией на поверхности.
Эти
углы называются полярным и азимутальным
соответственно.
между ортогональной проекцией луча
на поверхность и линией на поверхности.
Эти
углы называются полярным и азимутальным
соответственно.
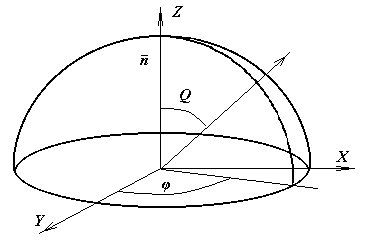
Рис. 9.1. Лучи отражения в системе координат нормали к поверхности
Они
позволяют нам определить направления
![]() и
и
![]() под которыми свет падает на поверхность
и излучается к наблюдателю (рис. 9.2).
под которыми свет падает на поверхность
и излучается к наблюдателю (рис. 9.2).
Определим
двух лучевую функцию отражательной
способности
(ДФОС), которая показывает изменение
яркости поверхности при заданных
направлениях наблюдения и освещения.
Количество света, падающего на поверхность
по направлению
(освещенность элементарного участка)
обозначим
![]() .
Яркость поверхности, наблюдаемая в
направлении
,
обозначим
.
Яркость поверхности, наблюдаемая в
направлении
,
обозначим
![]() .
ДФОС определится по формуле:
.
ДФОС определится по формуле:
![]() .
.
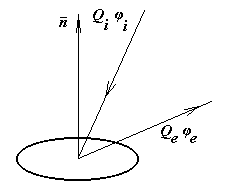
Рис. 9.2. Падающий луч и один из лучей отраженного потока
Для
многих поверхностей их яркость не
меняется при повороте поверхности
вокруг нормали. В этом случае ДФОС
зависит не от
![]() и
и
![]() по отдельности, а от их разности
по отдельности, а от их разности![]() -
-
![]() .
Это, в частности, верно для матовых и
зеркально отражающих поверхностей, но
не верно для поверхностей с ориентированной
микроструктурой, например для некоторых
минералов, (например, минерала тигровый
глаз),
или радужных перьев некоторых птиц. В
реальном случае могут существовать
несколько точечных или даже протяженных
источников, как например, лазерный зонд
и фоновое освещение. В случае протяженного
источника, чтобы получить ненулевое
излучение поверхности, мы должны
рассматривать ненулевой телесный угол.
Рассмотрим бесконечно малую площадку
размером
.
Это, в частности, верно для матовых и
зеркально отражающих поверхностей, но
не верно для поверхностей с ориентированной
микроструктурой, например для некоторых
минералов, (например, минерала тигровый
глаз),
или радужных перьев некоторых птиц. В
реальном случае могут существовать
несколько точечных или даже протяженных
источников, как например, лазерный зонд
и фоновое освещение. В случае протяженного
источника, чтобы получить ненулевое
излучение поверхности, мы должны
рассматривать ненулевой телесный угол.
Рассмотрим бесконечно малую площадку
размером
![]() по полярному и
по полярному и
![]() по азимутальному углам рис. 63.
по азимутальному углам рис. 63.
Эта
площадка задает телесный угол
![]() .
Если положить, что мощность излучения,
приходящего по направлению
.
Если положить, что мощность излучения,
приходящего по направлению
![]() на
единицу телесного угла, равняется
на
единицу телесного угла, равняется
![]() то мощность, идущая от рассматриваемой
площадки, будет равняться выражению
то мощность, идущая от рассматриваемой
площадки, будет равняться выражению
![]() ,
а полная освещенность поверхности —
выражению
,
а полная освещенность поверхности —
выражению
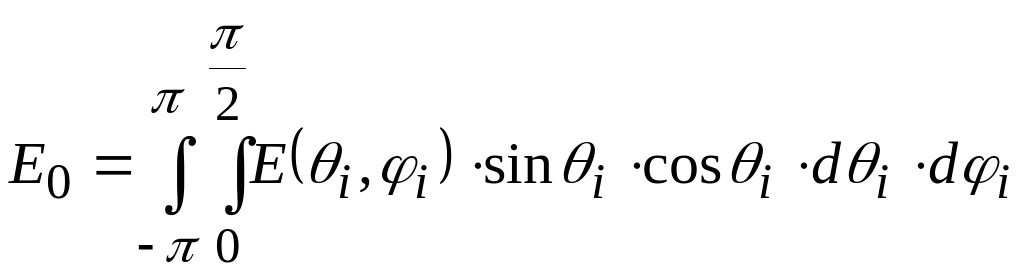 .
.
Для получения яркости поверхности объекта необходимо проинтегрировать произведение ДФОС и освещенности по полусфере возможных направлений падения света. Таким образом:
 .
.
Рис. 9.3. Падающий луч и один из лучей отраженного потока
Идеальной
ламбертовой поверхностью называется
такая поверхность, кажущаяся яркость
которой одинакова при любых направлениях
наблюдения и которая отражает все
падающие лучи, ничего не поглощая. Из
этого определения следует, что ДФОС (![]() )
для такой поверхности должна быть
константой. Проинтегрируем яркость
поверхности объекта по всем направлениям
и приравняем полученную таким образом
полную яркость полной освещенности.
)
для такой поверхности должна быть
константой. Проинтегрируем яркость
поверхности объекта по всем направлениям
и приравняем полученную таким образом
полную яркость полной освещенности.
 ,
или
,
или
 .
.
Используя
соотношение 2sin![]() cos
= sin2
,
получим
cos
= sin2
,
получим
![]() .
Итак, для идеальной ламбертовой
поверхности
.
Итак, для идеальной ламбертовой
поверхности![]() .
Заметим, что, поскольку ДФОС постоянна
для ламбертовой поверхности, мы можем
вычислить яркость L по освещенности
.
Заметим, что, поскольку ДФОС постоянна
для ламбертовой поверхности, мы можем
вычислить яркость L по освещенности
![]() т. е.
т. е.
![]() .
.
Модель идеальной ламбертовой и зеркальной поверхностей образуют как бы крайние точки в анализе отражающих свойств реальных поверхностей. Они часто используются при определении качества бумажного полотна и т. п. ДФОС можно определить экспериментально, освещая образец интересующего нас материала и измеряя его яркость с помощью сенсора. При этом контролируются углы падения излучения и угол наблюдения.
Рассмотрим использование выше сказанного на конкретном примере. Пусть необходимо обнаружить следы масляной пленки на материале близком по отражающим характеристикам к ламбертовой поверхности. Появление пленки сглаживает неровности и итоговая поверхность приобретает свойства зеркала. Таким образом пленка приводит к изменению формы ДФОС. Включая анализируемый участок материала в оптическую схему формирования изображения, получим оптический прибор с изменяемыми параметрами.
Поверхность
с пленкой – компонент оптической схемы,
расположенный вне зон промежуточных
изображений и играет роль отражающего
зеркала. Пусть в идеальном приборе с
зеркальной поверхность изображение
эталона (периодическая структура) имеет
вид отклика представленного на рис.
9.4. Не однородность отклика обусловлена
спецификой конкретной оптической схемы.
На рисунке
![]() - сигнал с CCD – многоэлементного
фотоприемника,
- номер фотоприемника по строке толщина
пленки указана в unit,
1 unit
примерно равен 0,18 мкм.
- сигнал с CCD – многоэлементного
фотоприемника,
- номер фотоприемника по строке толщина
пленки указана в unit,
1 unit
примерно равен 0,18 мкм.
Исходная поверхность без пленки рассеивает излучение и периодическая структура не прорабатывается (рис. 9.5). С появлением пленки появляется и изображение структуры, которое становится с ростом толщины пленки контрастнее (рис. 9.6, 9.7). Включение признака - контрастность позволяет решить задачу распознавания объектов подложка и подложка с пленкой.
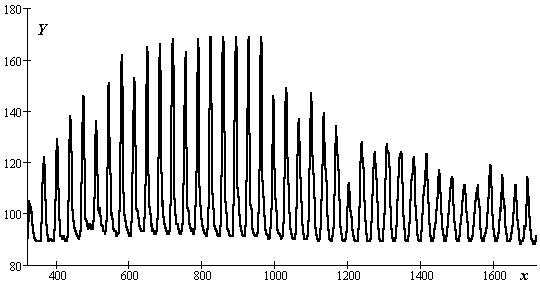
Рис. 9.4. Отклик от зеркальной поверхности

Рис. 9.5. Отклик от диффузионной рассеивающей поверхности (нет пленки)
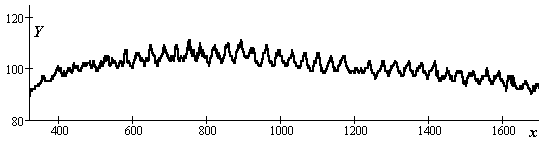
Рис. 9.6. Отклик от поверхности с пленкой в 10 unit
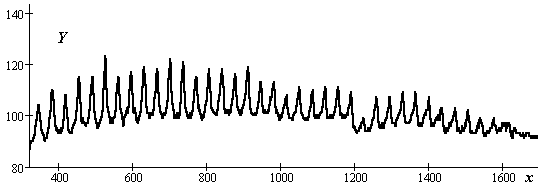
Рис. 9.7. Отклик от поверхности с пленкой в 20 unit
Для толстых пленок очень сильно влияние неплоскостности поверхности пленки. На рис.9.8 приведен вид поверхности пленки. В зоне плоской пленки – a сигнал по форме схож с калибровочным. Наклонные поверхности b, c, d приводят к потере энергии сигнала и к изменению формы сигнала.

Рис.9.8. Участки a,b,c,d поверхности пленки(эллипс в районе точки а – смещающаяся зона контроля)
Разность коэффициента отражения эталонного сигнала в расчетных зонах может служить флагом неплоской поверхности. На рис.9.9 приведены сигналы в расчетных зонах для пленки толщиной 80 unit. Отчетливо видно различие значительно лучшая проработка
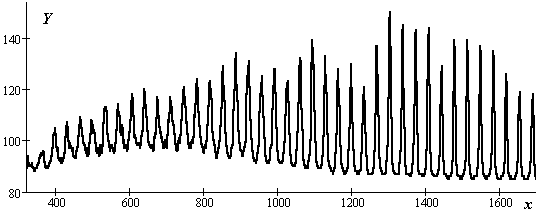
Рис. 9.9. Отклик от поверхности с неоднородной пленкой толщиной 80 unit
Это пример сложной задачи формирования признаков, в которой присутствует определенная физическая модель и сложные измерительные устройства, определяющие значения параметра косвенным путем.
