
- •Основные понятия,гипотизы и принципы
- •Метод сечений
- •Понятие о стержне, простые виды деформации
- •Понятие о напряжениях.
- •Инварианты. Виды напряженного состояния
- •Понятие о перемещениях при деформации. Линейные и угловые. Тензор деформации.
- •Главные деформации. Инварианты деформации.
- •Поперечные деформации коэфицент Пуассона
- •Обобщенный закон Гука
Главные деформации. Инварианты деформации.
Главными деформациями называют деформации на трехвзаимо перпендикулярных направлениях между которыми отсутствуют сдвиги.
 .
.
Поперечные деформации коэфицент Пуассона
Метода Гребенюка стр .53-54
Обобщенный закон Гука
Найдем линейную деформацию вдоль Ох.Она будет складываться из трех частей:
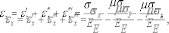
|
или
|
Аналогично можно определить линейные деформации по направлениям двух других осей:
|
|
В соответствии с законом Гука при сдвиге (3.14) связь между угловыми деформациями и касательными напряжениями можно представить независимо для каждой из
трех плоскостей, параллельных координатным плоскостям:
|
Таким образом, получены шесть формул, которые выражают линейную зависимость между составляющими деформации и напряжений в изотропном упругом теле и
называются обобщенным законом Гука:
Для определения удельной потенциальной энергии,накапливаемой изотропным материалом при линейно упругом деформирование, вырежем главными площадками из тела в окресности рассматриваемой точки еденичный объем. Используя обобщенный закон Гука получаем: ,ε1=(σ1-μ(σ2+σ3))/Ε, ε2=(σ2-μ(σ1+σ3))/Ε, ε3=(σ3-μ(σ1+σ2))/Ε Далее по методе гребенюка страница 56
Хрупкое и пластическое разрушение В начале мы ввели понятия о двух простейших типах разрушения:
1)
хрупком–
путем
отрыва от наибольших растягивающих
нормальных напряжений
2)
пластичном
–
путем сдвига от максимальных касательных
напряжений
Схематически эти условия показаны на рис.22.2 с помощью прямых 1-1 и 2-2. Свойство материала разрушаться пластически (вязко) или хрупко не является абсолютным. Каждое тело обладает тем и другим свойством в большей или меньшей степени в зависимости от температуры, внешнего давления, скорости нагружения, времени нагружения и др.
Рис. 22.2
Пусть напряженное состояние в точке тела описывается окружностью Мора 1 (рис. 22.2), которая касается вертикальной прямой 1-1 и не пересекает прямой 2-2, в этом случае произойдет хрупкое разрушение материала путем отрыва, и критерий разрушения запишется в виде:
Сопротивление
отрыву R
считается
постоянной величиной, не зависяшей
от вида напряженного состояния. Если
окружность Мора
Изложенная простая схема разрушения носит довольно грубый и приближённый характер в силу того, что разрушение является смешанным. Однако представление о существовании двух видов разрушения материалов путём сдвига и отрыва имело и имеет положительное методическое значение для объяснения физической стороны вопроса о разрушении.
Ещё
одним простейшим критерием хрупкого
разрушения материалов является
критерий наибольших удлинений
Сен-Венана, согласно которому предельное
состояние материала в частице тела
достигается тогда, когда максимальное
растягивающее удлинение
Для
хрупкого материала
где
величину
Данный критерий не нашёл на практике должного экспериментального подтверждения. Однако он в некоторых случаях даёт качественное подтверждение характера разрушения материалов. Например, при сжатии ряда горных пород возникают продольные трещины разрушения. При сжатии и выпучивании цилиндрической оболочки из дюраля возникают продольные трещины от окружного растяжения при отсутствии соответствующего растягивающего напряжения и др.
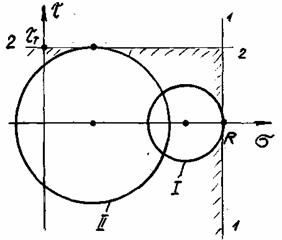
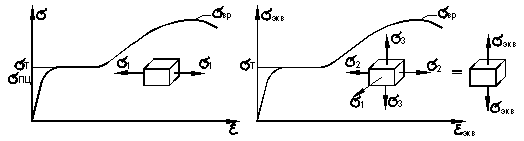
Условия пластичности и разрушения материалов Условия (критерии) пластичности и разрушения являются важными обобщениями понятий пределов текучести и прочности при одноосном растяжении (сжатии) на случай сложного напряжённого состояния (рис. 22.3).
Рис. 22.3
При одноосном растяжении предельные условия перехода в пластическое состояние и разрушение имеют соответственно вид (рис. 22.3)
а условие прочности –
Предположим, что для любого сложного напряжённого состояния можно найти ему равноопасное одноосное напряжённое состояние, осуществляемое некоторым эквивалентным напряжением
являющимся комбинацией главных напряжений. Тогда предельные условия при сложном напряжённом состоянии могут быть записаны в виде
а условие прочности –
Такая постановка задачи не является безупречной, но в то же время она удобна для ведения практических расчётов на прочность. Рассмотрим два критерия (условия) перехода тела из упругого состояния в неупругое или пластическое. Условие пластичности Сен-Венана.
Согласно
этому критерию свойство пластичности
материала при сложном напряжённом
состоянии начинает проявляться тогда,
когда максимальное касательное
напряжение достигает некоторого
предельного постоянного значения
В
случае простого растяжения предельное
условие имеет место при
В
случае чистого сдвига имеем
Сравнивая
(22.5) с (22.2) видим, что
Условие
пластичности (22.5) Сен-Венана достаточно
хорошо подтверждается экспериментами.
Его недостатком является то, что не
учитывает среднее главное напряжение
Условие (критерий) пластичности Мизеса. Согласно этому критерию материал переходит в пластическое состояние тогда, когда октаэдрическое касательное напряжение достигает некоторого предельного постоянного значения, т.е.
При
простом растяжении это условие
соответствует
Следовательно,
В
случае чистого сдвига
Условие
пластичности Мизеса (22.8) лучше
соответствует экспериментальным
данным, нежели условие пластичности
Сен-Венана (22.5). В отличие от последнего,
условие пластичности Мизеса учитывает
все три главных напряжения
Теория прочности Мора (1860г.)
Согласно
этой теории нарушение прочности
происходит тогда, когда на некоторой
площадке с нормалью
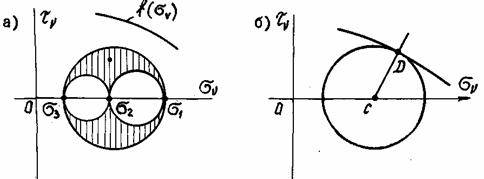
Чтобы сформулировать условие Мора (22.9) в терминах главных напряжений, воспользуемся кругами напряжений Мора.
Если
а) б) Рис. 22.4
Если
окружность большого круга Мора не
касается предельной кривой, как
показано на рис. 22.4, а,
то разрушения не произойдет. Если круг
Мора коснется предельной кривой
(рис.22.4, б),
то произойдет локальное разрушение.
Следовательно, становится ясным, как
построить предельную кривую
Это внесет некоторую погрешность в наши рассуждения.
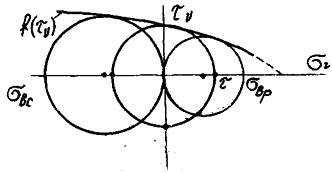
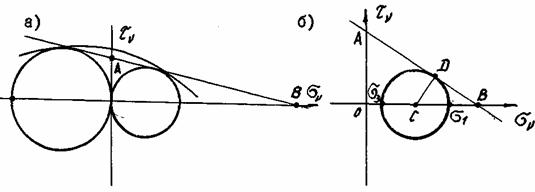
Рассмотрим
теперь произвольную предельную
окружность Мора, касающуюся предельной
прямой огибающей (рис. 22.6, б).
Из подобия треугольников АОВ и CDB
следует:
Рис. 22.5
Рис. 22.6
Поскольку
то
Так
как отрезки АО, ОВ, АВ - фиксированы,
то получаем связь между
В
случае растяжения в предельном
состоянии
принимает вид:
Условие прочности для хрупких материалов по Мору принимает вид:
где
Для
пластичных материалов (
|
|

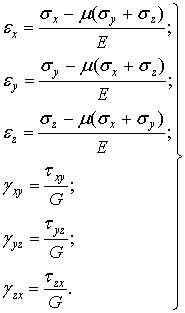
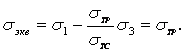 (22.12)
(22.12)