
- •Оглавление
- •Уравнение Лапласа и Пуассона.
- •Физический смысл стационарной задачи
- •Примеры
- •Понятие о потенциалах
- •Постановка задач
- •Первая и вторая формулы Грина с оператором , следствия.
- •Гармонические функции. Интегральное представление. Их основные свойства.
- •Примеры
- •Свойства гармонических функций.
- •Теорема о среднем для гармонических функций
- •Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле.
- •Следствия:
- •Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
- •Функция Грина для задачи с уравнением , понятия, определения.
- •Решение задач с её помощью
- •Построение функции Грина в одномерном случае на отрезке
- •Теория потенциалов, определение, основные свойства.
- •Объёмный потенциал
- •Потенциал простого слоя
- •Потенциал двойного слоя
- •Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
- •Сводная таблица6 общие сведения о потенциалах:
- •Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
- •Уравнение с оператором с особенностью , свойства, ограниченность, постановка задачи.
- •Уравнение Бесселя.
- •Особенность, построение ограниченного решения .
- •Общее решение, , , , понятие о функциях .
- •Асимптотика решений уравнения Бесселя, нули функции Бесселя.
- •Краевая задача на собственные значения: , её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
- •Модифицированное уравнение Бесселя, ограниченность решения , свойства, общее решение, понятие о функции .
- •Сводная таблица.
- •Краевая задача с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора .
- •Уравнение гипергеометрического типа.
- •Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).
- •Решение в виде полиномов. Формула Родрига.
- •Ортогональные решения полиномов. Свойства нулей.
- •Примеры: уравнения, краевые задачи, определение и свойства полиномов
- •Полиномы Лежандра.
- •Полиномы Чебышева-Лягера.
- •Чебышева-Эрмита.
- •Сводная таблица для уравнений гипергеометрического вида.
- •Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства.
- •Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных.
- •Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д.
Объёмный потенциал
Потенциал
поля, созданного зарядами, распределёнными
в области
с плотностью
![]() ,
равен
,
равен
![]() и называется объёмным потенциалом.
и называется объёмным потенциалом.
Свойство 1. Объёмный потенциал определён и непрерывен всюду.
Если
![]() ,
то интеграл
,
то интеграл
![]() не является не собственным. Поскольку
подынтегральная функция, как функция
,
непрерывна в точке
,
то непрерывен в этой точке и интеграл
.
не является не собственным. Поскольку
подынтегральная функция, как функция
,
непрерывна в точке
,
то непрерывен в этой точке и интеграл
.
Если
![]() ,
то, согласно теореме и замечанию,
достаточно доказать равномерную
сходимость, интеграла в окрестности
точки
.
Для этого оценим интеграл:
,
то, согласно теореме и замечанию,
достаточно доказать равномерную
сходимость, интеграла в окрестности
точки
.
Для этого оценим интеграл:
 ,
мы увеличили область, поместив всё в
шар
,
мы увеличили область, поместив всё в
шар
![]() ,
радиуса
,
радиуса
![]() .
Перейдём в последнем интеграле к
сферическим координатам и получим
тогда:
.
Перейдём в последнем интеграле к
сферическим координатам и получим
тогда:
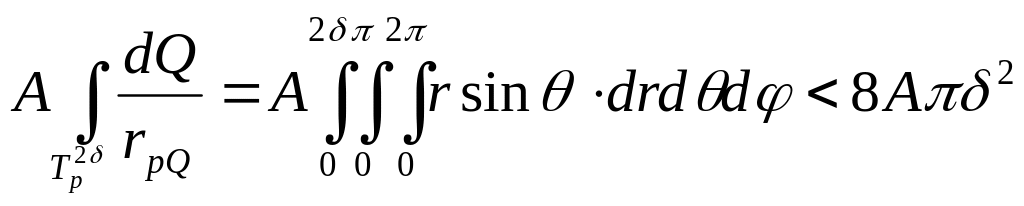 ,
чтобы интеграл был меньше заданного
,
достаточно взять
,
чтобы интеграл был меньше заданного
,
достаточно взять
![]() .
.
Свойство 2. Объёмный потенциал имеет всюду непрерывные частные производные первого порядка по координатам точки .
Если
,
то интеграл
не является не собственным. Поскольку
подынтегральная функция, как функция
точки
,
имеет в точке
непрерывные частные производные первого
порядка по координатам точки
,
то этим свойством обладает и интеграл
,
причём производные вычисляются путём
дифференцирования под знаком интеграла:
![]() ,
,
![]() ,
,
![]() - (1), где
- (1), где
![]() - координаты точки
.
- координаты точки
.
Если
,
то, согласно теореме и замечанию,
достаточно доказать равномерную
сходимость в окрестностях точки
интегралов от производных в правых
частях формул. Тогда законно
дифференцирование под знаком интеграла,
причём для производных
![]() ,
,
![]() и
и
![]() справедливы формулы (1). Для определённости
рассмотрим интеграл:
справедливы формулы (1). Для определённости
рассмотрим интеграл:
![]() .
Оценим его:
.
Оценим его:
 ,
т.к.
,
т.к.
![]() .
.
Далее,
 ,
достаточно взять
,
достаточно взять
![]() для того, чтобы выполнялось неравенство
для того, чтобы выполнялось неравенство
 .
.
Свойство
3. Объёмный
потенциал является гармонической
функцией вне области
,
в которой расположены заряды (массы).
Это свойство следует из того, что для
точек
![]() интеграл
не является не собственным, и поэтому
оператор Лапласа можно вносить под знак
интеграла:
интеграл
не является не собственным, и поэтому
оператор Лапласа можно вносить под знак
интеграла:
![]() ,
т.к. для точек
(а
точнее P≠Q)
имеем
,
т.к. для точек
(а
точнее P≠Q)
имеем
![]() .
.
Свойство
4. в точках
области
объёмный потенциал удовлетворяет
соотношению:
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() .
.
Вторые производные рвутся.
Свойство 5. При стремлении точки наблюдения к бесконечности объёмный потенциал стремится к нулю ( - огр.).
Применим
теорему о среднем:
![]() ,
где
,
где
![]() - суммарный заряд. Т.о.
- суммарный заряд. Т.о.
![]() .
.
Потенциал простого слоя
Потенциал
поля, созданного зарядами, распределёнными
по поверхности
![]() с плотностью
,
равен
с плотностью
,
равен
![]() и называется потенциалом простого слоя.
и называется потенциалом простого слоя.
Свойство 1. Потенциал простого слоя определён всюду.
Если
![]() (не принадлежит несущей поверхности
),
это очевидно, т.к.
(не принадлежит несущей поверхности
),
это очевидно, т.к.
![]() имеет
конечное значение для любых р.
имеет
конечное значение для любых р.
Если
![]() ,
то интеграл
является несобственным по двумерной
области
.
Из математического анализа известно,
что несобственный интеграл по двумерной
области
,
то интеграл
является несобственным по двумерной
области
.
Из математического анализа известно,
что несобственный интеграл по двумерной
области
![]() абсолютно сходится, если
абсолютно сходится, если
![]() ,
в нашем случае
,
в нашем случае
![]() ,
следовательно, интеграл сходится.
,
следовательно, интеграл сходится.
Свойство 2. Потенциал простого слоя и непрерывен всюду.
Если
![]() ,
то интеграл
не является не собственным, и его
непрерывность следует из непрерывности
подынтегральной функции
,
то интеграл
не является не собственным, и его
непрерывность следует из непрерывности
подынтегральной функции
![]() .
.
Если
![]() ,
то, согласно теореме и замечанию,
достаточно доказать равномерную
сходимость, интеграла в окрестности
точки
.
Для этого оценим интеграл
,
то, согласно теореме и замечанию,
достаточно доказать равномерную
сходимость, интеграла в окрестности
точки
.
Для этого оценим интеграл
![]() по части поверхности
по части поверхности
![]() ,
содержащей точку
,
содержащей точку
![]() и имеющей диаметр меньший, чем
и имеющей диаметр меньший, чем
![]() .
Пусть
.
Пусть
![]() - произвольная точка, причем:
- произвольная точка, причем:
![]() .
Пусть
.
Пусть
![]() - проекция поверхности
- проекция поверхности
![]() на
плоскость
на
плоскость
![]() ,
а
,
а
![]() круг на плоскости
с центром в точке
круг на плоскости
с центром в точке
![]() радиуса
.
Проекция на плоскость
элемента поверхности
радиуса
.
Проекция на плоскость
элемента поверхности
![]() равна:
равна:
![]() .
Оценим:
.
Оценим:
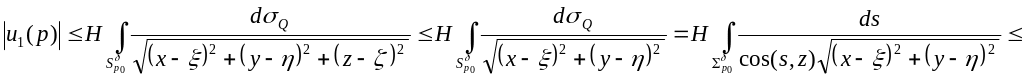
![]() вводим
полярную систему координат с началом
в точке
вводим
полярную систему координат с началом
в точке
![]() ,
тогда легко вычислить последний интеграл,
он равен:
,
тогда легко вычислить последний интеграл,
он равен:
 .
.
Достаточно
взять
для того, чтобы выполнялось неравенство
![]() .
.
Свойство 3. Потенциал простого слоя является гармонической функцией всюду, кроме точек несущей поверхности .
Это
свойство очевидно, так как для точек
![]() интеграл
не является несобственным и поэтому:
интеграл
не является несобственным и поэтому:
![]()
Свойство
4. нормальные
производные потенциала простого слоя
имеют разрыв первого рода в точках
поверхности
со скачком
![]() .
.
![]()
Свойство 5. если несущая поверхность ограничена, то потенциал простого слоя стремится к нулю, когда точка стремится к бесконечности.
Применим
к интегралу теорему о среднем:
![]() ,
где
,
где
![]() - суммарный заряд.
- суммарный заряд.
Т.о.
