
- •Оглавление
- •Уравнение Лапласа и Пуассона.
- •Физический смысл стационарной задачи
- •Примеры
- •Понятие о потенциалах
- •Постановка задач
- •Первая и вторая формулы Грина с оператором , следствия.
- •Гармонические функции. Интегральное представление. Их основные свойства.
- •Примеры
- •Свойства гармонических функций.
- •Теорема о среднем для гармонических функций
- •Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле.
- •Следствия:
- •Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
- •Функция Грина для задачи с уравнением , понятия, определения.
- •Решение задач с её помощью
- •Построение функции Грина в одномерном случае на отрезке
- •Теория потенциалов, определение, основные свойства.
- •Объёмный потенциал
- •Потенциал простого слоя
- •Потенциал двойного слоя
- •Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
- •Сводная таблица6 общие сведения о потенциалах:
- •Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
- •Уравнение с оператором с особенностью , свойства, ограниченность, постановка задачи.
- •Уравнение Бесселя.
- •Особенность, построение ограниченного решения .
- •Общее решение, , , , понятие о функциях .
- •Асимптотика решений уравнения Бесселя, нули функции Бесселя.
- •Краевая задача на собственные значения: , её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
- •Модифицированное уравнение Бесселя, ограниченность решения , свойства, общее решение, понятие о функции .
- •Сводная таблица.
- •Краевая задача с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора .
- •Уравнение гипергеометрического типа.
- •Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).
- •Решение в виде полиномов. Формула Родрига.
- •Ортогональные решения полиномов. Свойства нулей.
- •Примеры: уравнения, краевые задачи, определение и свойства полиномов
- •Полиномы Лежандра.
- •Полиномы Чебышева-Лягера.
- •Чебышева-Эрмита.
- •Сводная таблица для уравнений гипергеометрического вида.
- •Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства.
- •Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных.
- •Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д.
Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле.
Теорема о максимумах и минимумах. Любая функция, гармоническая в области D и непрерывная на Г принимает своё максимальное и минимальное значения на границах и только на границах (за исключением тривиального случая U=const).
Доказательство:
пусть теорема не верна.
![]() -
максимум достигается во внутренней
точке. Применим теорему о среднем:
-
максимум достигается во внутренней
точке. Применим теорему о среднем:
![]() ,
видим, что:
,
видим, что:
![]() .
.
Вычтем:
![]() ,
но
,
но
![]() значит
что разность
значит
что разность
![]() всегда, а
всегда, а
![]() от
неотрицательной непрерывной функции
равен нулю в случае если
от
неотрицательной непрерывной функции
равен нулю в случае если
![]() на сфере
на сфере
![]() ,
то есть получили, что максимум достигается
на границе сферы
,
и в то же время в самой точке Р. В силу
произвольности выбора точки Р и радиуса
R
максимальное значение достигается во
всей области D
и в том числе на границе. Т.о. пришли к
исключающему варианту теоремы (получен
тривиальный случай). Следовательно,
максимум достигается только на границе.
,
то есть получили, что максимум достигается
на границе сферы
,
и в то же время в самой точке Р. В силу
произвольности выбора точки Р и радиуса
R
максимальное значение достигается во
всей области D
и в том числе на границе. Т.о. пришли к
исключающему варианту теоремы (получен
тривиальный случай). Следовательно,
максимум достигается только на границе.
Чтд.
Теорема о минимумах доказывается аналогично, заменой (u) на (-u).
Следствия:
1. Единственность. Задача Дирихле имеет единственное решение, если её однородная задача имеет только тривиально решение.
Рассмотрим
первую краевую задачу Дирихле.
![]() .
Пусть задача Дирихле имеет два решения:
.
Пусть задача Дирихле имеет два решения:
![]() ,
тогда:
,
тогда:
![]() из
теоремы о mах
и min
следует, что
из
теоремы о mах
и min
следует, что
![]() - во всей
области D
в том числе и на границе.
- во всей
области D
в том числе и на границе.
2. Корректность - непрерывная зависимость решений от дополнительных условий в любой конечной точке области.
Если
имеем уравнение
![]() и два условия
и два условия
![]() ,
причём
,
причём
![]() (отличные на малую величину), то и
(отличные на малую величину), то и
![]() (тоже мало отличаются). Докажем.
(тоже мало отличаются). Докажем.
Пусть
![]() ,
-
гармоническая функция, тогда:
,
-
гармоническая функция, тогда:![]()
![]() ,
тогда по теореме о максимумах и минимумах
везде в области D
верно:
,
тогда по теореме о максимумах и минимумах
везде в области D
верно:
![]()
![]() то есть малому изменению граничных
условий отвечает малое изменение
решений. Задача Дирихле корректна.
то есть малому изменению граничных
условий отвечает малое изменение
решений. Задача Дирихле корректна.
Пример
некорректной задачи:
![]() -
уравнение Лапласа. Рассмотрим задачу
Коши:
-
уравнение Лапласа. Рассмотрим задачу
Коши:
 .
.
Рассмотрим
два типа начальных условий:
 .
Эти граничные условия мало отличаются
при
.
Эти граничные условия мало отличаются
при
![]() .
Но решения не будут близкими при этом:
.
Но решения не будут близкими при этом:
 ,
т.к.
,
т.к.
![]() .
Таким образом, решения будут различны
при больших n.
.
Таким образом, решения будут различны
при больших n.
Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
(1) Точка р принадлежит области D, ограниченной контуром Г.
Воспользуемся
формулой:
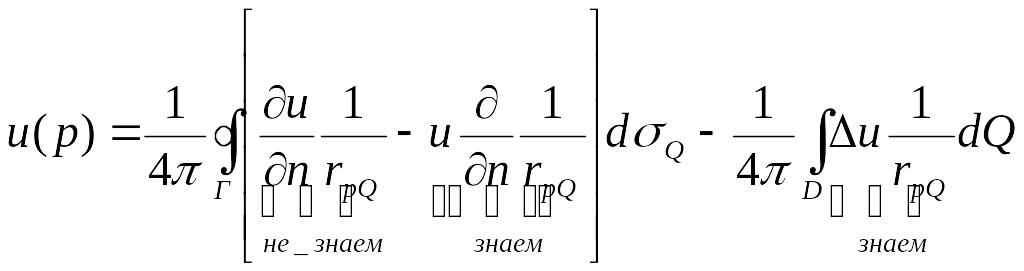 ,
мы не знаем, как находится
,
мы не знаем, как находится
![]() и, соответственно, не можем найти точное
решение - избавимся от слагаемого,
которое её содержит. Воспользуемся
второй формулой Грина для функций
и
и, соответственно, не можем найти точное
решение - избавимся от слагаемого,
которое её содержит. Воспользуемся
второй формулой Грина для функций
и
![]() .
Из второй формулы Грина следует
.
Из второй формулы Грина следует
![]() .
.
В
качестве w
выберем любую гармоническую функцию в
D,
такую что:
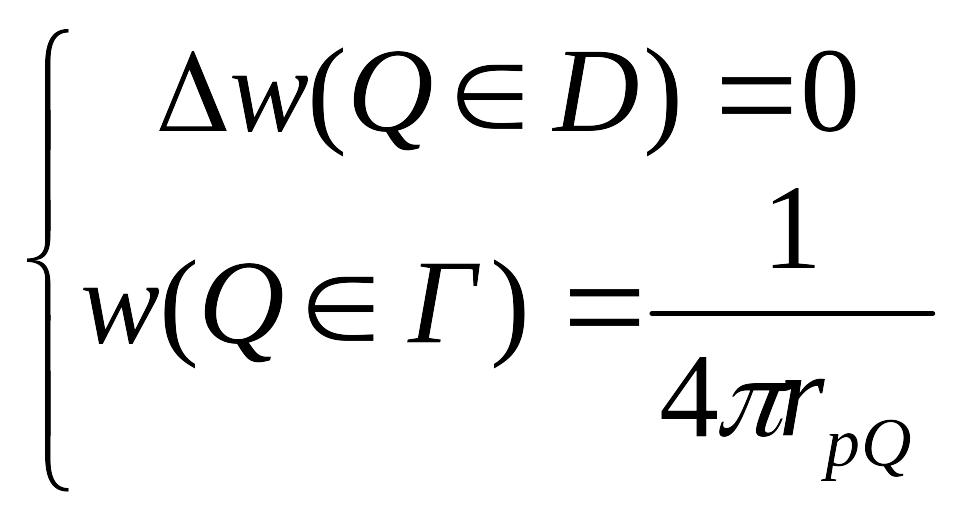 ,
то есть мы выбираем её так, чтобы на
границе она совпадала с
,
то есть мы выбираем её так, чтобы на
границе она совпадала с
![]() .
.
Вычитая
два этих выражения, получаем:
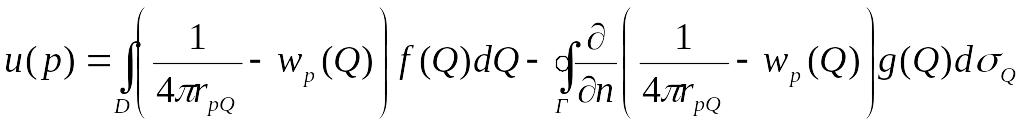 .
Пусть
.
Пусть
![]() ,
тогда:
,
тогда:
![]() ,
,
![]() -
функция Грина задачи Дирихле.
-
функция Грина задачи Дирихле.
Функция
Грина является решением задачи (1),
удовлетворяет уравнению:
![]() .
Проинтегрируем по шару:
.
Проинтегрируем по шару:
|
|
Функция
Грина задачи
,
это решение следующей задачи:
![]() .
.
Её
физический смысл. Рассмотрим заряд
величины
![]() в точке р, его потенциал в точке Q:
в точке р, его потенциал в точке Q:
![]() ,
функция
подправляет его так, чтобы на границе
он равнялся нулю. Если представить, что
этот заряд находиться внутри шара,
сделанного из металлической сетки, то
можно сказать, что
моделирует заземление.
,
функция
подправляет его так, чтобы на границе
он равнялся нулю. Если представить, что
этот заряд находиться внутри шара,
сделанного из металлической сетки, то
можно сказать, что
моделирует заземление.
Функция
Грина в двухмерном случае:
![]() .
Мы получили решение задачи (1) через
функцию Грина, но саму функцию Грина не
нашли, для этого надо решить задачу для
,
найти
.
Пусть точка
.
Мы получили решение задачи (1) через
функцию Грина, но саму функцию Грина не
нашли, для этого надо решить задачу для
,
найти
.
Пусть точка
![]() принадлежит
области
принадлежит
области
![]() ,
ограниченной
,
ограниченной
![]() .
Ищем
.
Ищем
![]() виде потенциала:
виде потенциала:
![]() подбираем
точки
подбираем
точки
![]() ,
сажаем в них заряды
,
сажаем в них заряды
![]() ,
так чтобы суммарный потенциал на границе
был = 0 – метод электростатических
изображений.
,
так чтобы суммарный потенциал на границе
был = 0 – метод электростатических
изображений.
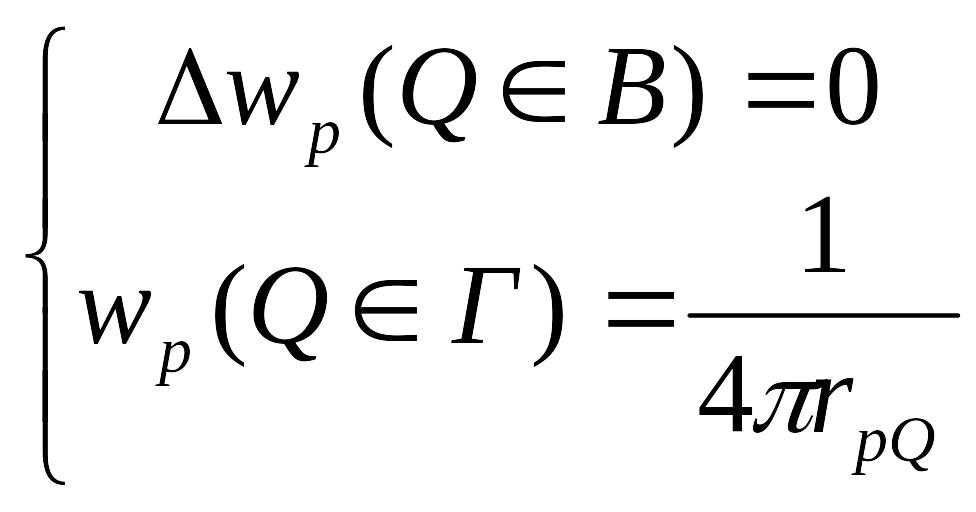 .
.


