3. Гармонические функции. Интегральное представление. Их основные свойства.

(p) - гармоническая функция – если она удовлетворяет уравнению Лапласа: , и непрерывна в .

Примеры

1: Линейная функция вида - гармоническая функция, т.к. удовлетворяет условиям.

2: Цилиндрические функции. Рассмотрим цилиндрическую систему координат (r,φ,z): и , тогда , если , то останется первое слагаемое: =0, решаем . Т.о. функция вида - гармоническая функция в т. .

3: Сферические функции. Рассмотрим сферические координаты: и , тогда , если , то останется первое слагаемое: , решаем т.о. функция вида - гармоническая функция в т. .

Получим формулу интегрального представления.

Пусть , тогда (согласно второй формуле Грина) получаем: . Эта формула верна в случае любых двух непрерывно дифференцируемых функций в области D, а выбираем следующим образом: , (причём заметим, что - гармоническая функция), имеет особенность в области D в точке P = Q. Вырежем её из области D: окружим её окружностью с центром в точке Р и радиусом - . Т.о. формула справедлива в области и появится ещё одно слагаемое: - интеграл по сфере , тогда: .

Рассмотрим последний интеграл:

Применим к первому слагаемому теорему о среднем: , - точка на сфере . Перейдём к переделу : - первое слагаемое исчезло. Рассмотрим второе слагаемое: применим теорему о среднем , - точка на сфере , Перейдём к переделу : . Второе слагаемое: . Тогда второй интеграл перепишется в виде: , а интеграл , так как .

(Примечание: когда мы окружали окрестностью точку р, это должно было отразится и на объёмном интеграле, но при этот интеграл становится несобственный, но сходящийся. Тогда ).

Таким образом, получили, что: , выражаем . Мы получили формулу для 3D случая (к(р) положим = 1) : .

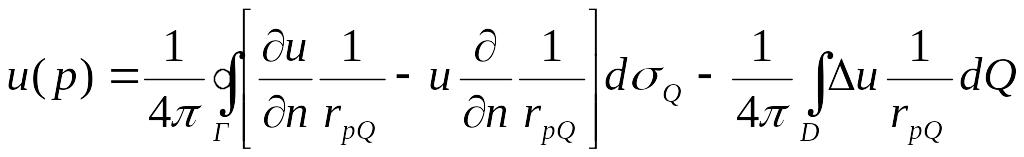В двумерном случае получаем аналогично: ,

- расстояние между точками p и Q.

Свойства гармонических функций.

1. Гармоническая функция бесконечно дифференцируема в любых внутренних точках.

2. - интеграл по любой замкнутой поверхности внутри области гармоничности D. Следует из второй формулы Грина. Стационарное распределение возможно лишь тогда, когда тепловой поток равен нулю.

3. Теорема о среднем. Для любой гармонической функции в области D:

- равен своему среднему значению по любой сфере .

4. Теорема о максимумах и минимумах. Любая функция, гармоническая в области D и непрерывная на Г принимает своё максимальное и минимальное значения на границах и только на границах (кроме U=const).

4. Теорема о среднем для гармонических функций

Теорема о среднем: Для любой гармонической функции в области D выполняется: - равна своему среднему значению по любой сфере с центром в точке р и радиусом R - .

Доказательство: запишем интегральную формулу:

Учтём что, . Функция - гармоническая в области D, тогда . Последний интеграл исчез. Воспользуемся первым свойством гармонических функций: интеграл по любой замкнутой поверхности внутри области гармоничности D равен нулю. Тогда получаем что, . Первый интеграл исчез. Рассмотрим второй интеграл, учтём, что производная по нормали совпадает с производной по радиусу: .

Чтд.