19. Сводная таблица для уравнений гипергеометрического вида.

	Лежандр			Чебышев - Лягер		Чебышев - Эрмит
Вид уравнения
Упрощенное уравнение
Собственные решения:
Собственные функции
Рекуррентные соотношения:
Производящие функции:
Ортогональность и норма:
Упрощенное уравнение гипергеометрического вида:
его самосопряжённый вид
Произвольное решение уравнения гипергеометрического вида тоже является решением другого уравнения гипергеометрического вида:			Пусть:
Собственные решения:
Собственные функции (Формула Родрига):
Ортогональность:
Присоединённые уравнение Лежандра:		Присоединённые функции: ,			Норма присоединённых функций:

15. Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства.

Рассмотрим задачу: найти собственные значения и собственные функции уравнения (1) при условии ограниченности (2) . Ищем решение в виде: . Подставим в уравнение: . Это же уравнение получается для производной решения уравнения Лежандра : , если его продифференцировать раз. Нетривиальное ограниченное решение уравнения Лежандра существует лишь при , где - целое положительное число. Отсюда следует, что есть решение уравнения (2), а функция - есть собственная функция задачи (1), соответствующая собственному значению . - присоединённая функция Лежандра -го порядка.

Свойства.

1) Норма присоединённых функций: .

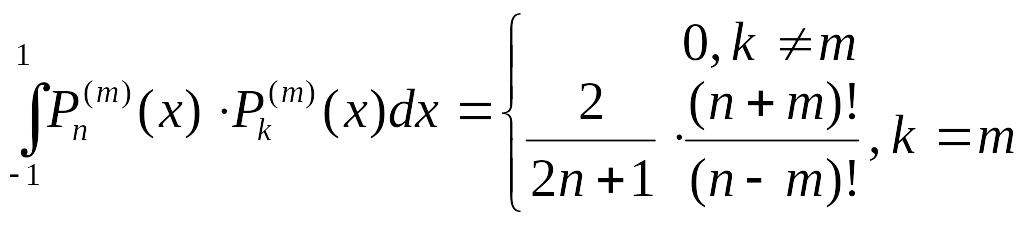2) Любая функция , непрерывная на отрезке и обращающаяся в нуль на его концах при и , может быть равномерно аппроксимирована с любой степенью точности линейной комбинацией из присоединённых функций любого порядка .

16. Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных.

Запишем оператор Лапласа в сферических координатах:

: .

Решим уравнение Лапласа (1) методом разделения переменных. Ищем решение в виде: , подставим: (2) . Запишем задачу для (функции не имеют особенности и определены на сфере).: (3) Задача: найти значения , при которых задача (3) имеет нетривиальное решение. Сферическими функциями называются любые нетривиальные решения задачи (3). Будем решать задачу (3) методом разделения переменных. Пусть , подставляем, домножив на , получаем: , получаем две задачи: и (5) .

Решаем (4). или (тоже самое) , для того чтобы выполнялась периодичность должно быть целым: . Тогда .

Решаем (5). Сделаем замену: , учтем что тогда . Делим (5) на : , получили уравнение для присоединённых полиномов Лежандра. Тогда .

П

m

олучили, что каждой паре целых чисел при условии соответствует:

- полный набор базисных сферических функций. Каждому соответствует и базисных функций.

Перейдём к решению задачи для : . Ищем решение в виде: , подставляем: - шаровый функции,

тогда , - решение уравнения Лапласа в сферических координатах.