
- •Оглавление
- •Уравнение Лапласа и Пуассона.
- •Физический смысл стационарной задачи
- •Примеры
- •Понятие о потенциалах
- •Постановка задач
- •Первая и вторая формулы Грина с оператором , следствия.
- •Гармонические функции. Интегральное представление. Их основные свойства.
- •Примеры
- •Свойства гармонических функций.
- •Теорема о среднем для гармонических функций
- •Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле.
- •Следствия:
- •Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
- •Функция Грина для задачи с уравнением , понятия, определения.
- •Решение задач с её помощью
- •Построение функции Грина в одномерном случае на отрезке
- •Теория потенциалов, определение, основные свойства.
- •Объёмный потенциал
- •Потенциал простого слоя
- •Потенциал двойного слоя
- •Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
- •Сводная таблица6 общие сведения о потенциалах:
- •Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
- •Уравнение с оператором с особенностью , свойства, ограниченность, постановка задачи.
- •Уравнение Бесселя.
- •Особенность, построение ограниченного решения .
- •Общее решение, , , , понятие о функциях .
- •Асимптотика решений уравнения Бесселя, нули функции Бесселя.
- •Краевая задача на собственные значения: , её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
- •Модифицированное уравнение Бесселя, ограниченность решения , свойства, общее решение, понятие о функции .
- •Сводная таблица.
- •Краевая задача с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора .
- •Уравнение гипергеометрического типа.
- •Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).
- •Решение в виде полиномов. Формула Родрига.
- •Ортогональные решения полиномов. Свойства нулей.
- •Примеры: уравнения, краевые задачи, определение и свойства полиномов
- •Полиномы Лежандра.
- •Полиномы Чебышева-Лягера.
- •Чебышева-Эрмита.
- •Сводная таблица для уравнений гипергеометрического вида.
- •Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства.
- •Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных.
- •Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д.
Сводная таблица.
Лапласиан в цилиндрических координатах: |
|
Лапласиан в сферических координатах: |
|
Уравнение Бесселя: (уравнение для цилиндрических функций) |
|
решение
уравнения Бесселя при
|
|
Функция Бесселя первого рода: |
|
Модифицированное уравнение Бесселя: |
|
Модифицированная функция Бесселя: |
|
Функция Неймана: |
|
Функции Ханкеля: |
;
|
Функция Макдональда: |
|
рекуррентные соотношения: |
1) 2)
|
функция Бесселя полуцелых порядков: |
|
рассмотрим краевую задачу (задачу на собственные значения и собственные функции): |
|
Ортогональность (и нормировка): |
|
Краевая задача с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора .
Рассмотрим
уравнение: (*)
и пусть
![]() - имеет два ноля.
- имеет два ноля.
|
Известно
ограниченное решение в точке b,
а также ограниченное решение в точке
a.
Возможен случай, когда решение в точке
перейдёт в ограниченное решение в
точке
|
Полученные
функции, отвечающие различным собственным
значениям, будут ортогональны, то есть
оператор
![]() должен быть самосопряжённым.
должен быть самосопряжённым.
Самосопряженность
оператора
![]()
Используя
2-ую формулу Грина получаем:
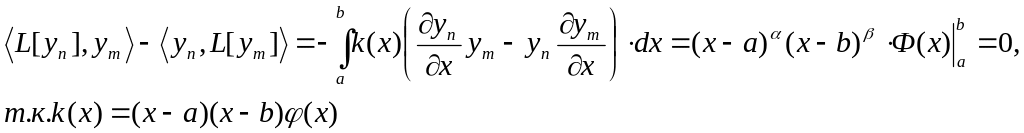
Уравнение гипергеометрического типа.
Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).
Рассмотрим
уравнение: (1)![]() - уравнение
гипергеометрического вида,
где
- уравнение
гипергеометрического вида,
где
![]() - полиномы порядка
- полиномы порядка
![]() ,
а
,
а
![]() - полиномы порядка
- полиномы порядка
![]() .
.
Домножим
(1) на
![]() ,
подобрав её так, чтобы уравнение (1)
приняло самосопряжённый вид:
,
подобрав её так, чтобы уравнение (1)
приняло самосопряжённый вид:![]() .
Для этого нужно, чтобы
.
Для этого нужно, чтобы
![]() - дифференциальное уравнение для
,
тогда получим: (1*)
- дифференциальное уравнение для
,
тогда получим: (1*)![]() - самосопряжённый вид уравнения (1).
Определим
:
- самосопряжённый вид уравнения (1).
Определим
:
![]() -
весовые функции.
-
весовые функции.
Это
свойство одномерной задачи. Т.к. вид
оператора
![]() отличается от
отличается от
![]() .
Самосопряжённая форма (*) большое
ограничение.
.
Самосопряжённая форма (*) большое
ограничение.
Решение в виде полиномов. Формула Родрига.
Пусть
![]() - решение уравнения
.
Продифференцируем:
- решение уравнения
.
Продифференцируем:
![]() .
Обозначим
.
Обозначим
![]() ,
тогда
,
тогда
![]() .
Производная
решения гипергеометрического вида тоже
является решением другого уравнения
гипергеометрического вида.
Далее можно повторить это действие,
введя аналогичную замену:
.
Производная
решения гипергеометрического вида тоже
является решением другого уравнения
гипергеометрического вида.
Далее можно повторить это действие,
введя аналогичную замену:
![]() и т.д. Следовательно
и т.д. Следовательно
![]() - решение различных уравнений
гипергеометрического вида.
- решение различных уравнений
гипергеометрического вида.
Определим
коэффициенты
![]() и
и
![]() .
Посмотрим, как они изменятся дальше.
.
Посмотрим, как они изменятся дальше.
![]() ,
,
![]() .
.
Запишем:
![]() ,
дифференцируем:
,
дифференцируем:
![]() .
.
![]() .
Найдем
.
Найдем
![]() .
Рассмотрим
.
Рассмотрим
![]() - сложим все эти разности и получим:
- сложим все эти разности и получим:

Таким
образом:
 .
Приведём (2) к самосопряжённому виду.
(2) – уравнение для производных. (2*)
.
Приведём (2) к самосопряжённому виду.
(2) – уравнение для производных. (2*)![]() ,
где
,
где
![]() - весовые функции.
- весовые функции.
Каждому
целому
![]() можно указать такие значения
можно указать такие значения
![]() ,
что
,
что
![]() .
Т.е.
.
Т.е.
![]() ,
при таком выборе
,
при таком выборе
![]() ,
уравнение
,
уравнение
![]() приобретает новые качества:
и новый вид
приобретает новые качества:
и новый вид
![]() .
Тогда
.
Тогда
![]() ,
положим эту константу равной нулю, тогда
,
положим эту константу равной нулю, тогда
![]() - многочлен степени
.
Таким образом, мы нашли бесконечную
цепочку полиномов – решений уравнения
при соответствующих значения
.
Это система
- многочлен степени
.
Таким образом, мы нашли бесконечную
цепочку полиномов – решений уравнения
при соответствующих значения
.
Это система
![]() - нормальная система полиномов образует
базис. Вспомним
,
перепишем в виде:
- нормальная система полиномов образует
базис. Вспомним
,
перепишем в виде:
![]() .
Рассмотрим
.
Рассмотрим
![]()
![]() .
Для
.
Для
![]() воспользуемся
при
воспользуемся
при
![]() пока
пока
![]() (т.е. пока можно делить)
(т.е. пока можно делить)
 .
.
Запишем
в чистом виде:
![]() - формула Родрига.
- формула Родрига.



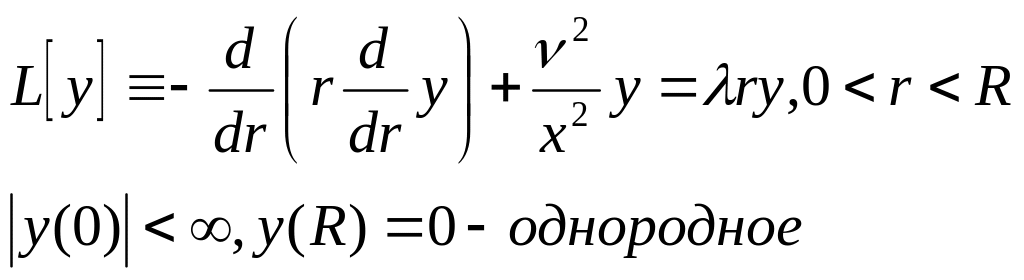
 ,
где
,
где

