Уфимский Государственный Авиационный Технический Университет

Отчет по лабораторной работе №3

“Пересечение прямой и плоскости и видимость прямой ”

По дисциплине Компьютерная графика.

Выполнил

студент гр. МО-316а

Сахибгареев К.И.

Проверил

Верхотуров М. А.

Уфа 2008

Содержание

1. Содержательная и формальная постановка задачи.

2. Структура решения.

3. Обзор и анализ методов решения.

4. Описание реализации применяемых методов.

5. Описание программного обеспечения (руководство программиста).

6. Руководство пользователя.

7. Результаты.

1.Содержательная и формальная постановка задачи

Содержательная постановка задачи:разработать программу, реализующую отображение отрезка, заданного двумя точками, и плоскости, заданной тремя точками, и их проекций в трёх- и двумерном чертежах на экране компьютера с возможностью изменять координаты точек.

Формальная постановка задачи: разработать программу, реализующую вывод на экран

аксонометрического чертежа (первый октант) с изображением отрезка A1A2и плоскости (заданной треугольникомP1P2P3) с изображением точки их пересеченияK,

комплексного чертежа (6ез профильной проекции) с изображением проекций отрезка, плоскости, точки пересечения и линий связи (для всех 6 точек)

ползунковые переключатели (3 шт.) для интерактивного изменения координат (x,y,z) A1, A2, P1, P2, P3точек и точки наблюденияC(с возможностью выбора одной из 6 исходных точек для которой в текущий момент времени будет осуществляться изменение координат).

Переключатель w=0; w=1для смены ортогонального проецирования на центральное.

2.Структура решения

1. Вычисление точки пересечения

2. Определение видимости отрезка

3. Проецирование

3. Прорисовка

4. Примечание

3.Обзор и анализ методов решения

1. Вычисление точки пересечения

Рассмотрим решение задачи пересечения прямой и плоскости.

Прямая может быть:

1)параллельна плоскости,

2)лежать в этой плоскости,

3)пересекать эту плоскость.

Примечание: В дальнейшем под словом “Прямая” часто будет подразумеваться отрезок образованный точками A1,A2.

С другой стороны, прямая может быть вырождена в точку и нужно рассмотреть задачу о принадлежности точки плоскости, плоскость также может быть вырождена в прямую или в точку. При алгоритмическом рассмотрении этого вопроса должны быть рассмотрены все возможные комбинации.

Случай “Плоскость-это плоскость и Прямая-это прямая”:

Плоскость образуется тремя точками, тогда если эти точки совпадают, то плоскость вырождается в точку.

Задана плоскость ax+by+cz+d=0 или [xyz1][A]=0, где [A]=[abcd]. Любая тока трёхмерного пространства представима в однородных координатах вектором: [S]=[xyz1].

Если точка лежит на плоскости, то выполняется равенство [S][A]=0.

Если Sне лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка.

Рассмотрим параметрическое представление отрезка [P1,P2],t– параметр.

p(t)=P1+(P2-P1)t, 0<=t<=1, гдеt– расстояние междуP1 иP2.

Вектор vточки на отрезке можно представить в таком виде:v=s+dt, гдеs– начальная точка,d– направление отрезка.

Так как скалярное произведение точки на параметры плоскости равно 0, когда точка принадлежит плоскости, то получаем уравнение v*[A]=0.

S*[A]+dt[A]=0 – решая это уравнение относительноt, находим значение параметра, соответствующее точке пересечения. Исходя из уравнений:

x(t)=x1+(x2-x1)t

y(t)=y1+(y2-y1)t

z(t)=z1+(z2-z1)t

находим координаты точки пересечения прямой и плоскости.

Коэффициенты плоскости рассчитываются следующим образом:

Метод Ньюэла (вычисление коэффициентов (a, b, c , d) плоскости , заданнойn вершинами, в общем случае, не лежащих на одной плоскости)

, гдеif i=n then j=1 else j=i+1,k - любая точка на плоскости

При определении методом Ньюэла (суть которого – усреднение векторных произведений рёбер, исходящих из вершин многоугольника) мы в зависимости от последовательности обхода точек контура многоугольника можем получить 1 и ту же плоскость, но нормаль у неё может быть направлена в две противоположные стороны.

Случай “Плоскость-это плоскость и Прямая-это точка”:

“Прямая-точка” лежит на плоскости если скалярное произведении ее координат на коэффициенты плоскости равно нулю, т.е. [M][A]=0

Случай “Плоскость-это прямая и Прямая-это прямая”:

В этом случае точка пересечения находится с помощью решения системы из двух уравнений, каждое, из которых задает прямую. Решить систему можно, например, методом Крамера:

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде:

,

где

.

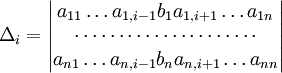(i-й столбец матрицы системы заменяется столбцом свободных членов).

После нахождения точки пересечения прямых необходимо проверить принадлежит ли эта точка пересечения отрезку A1A2:

Принадлежность определяется на основании правила треугольника. |MaxLen-SumNotMax| = 0, (*)

где MaxLen– длина наибольшей стороны,

SumNotMax– сумма длин двух других сторон.

Тогда точка принадлежит прямой, если выполняется (*) и Len(MN) =MaxLen, иначе точка не принадлежит прямой.

Случай “Плоскость-это прямая и Прямая-это точка”:

Принадлежность точки прямой проверяется простой подстановкой координат точки в уравнение прямой. Если получаем верное равенство, значит точка принадлежит прямой.

Случай “Плоскость-это точка и Прямая-это прямая”:

Точка принадлежит отрезку, если сумма расстояний от этой точки до конечных точек отрезка равна длине отрезка.

Случай “Плоскость-это точка и Прямая-это точка”:

Если все координаты точек плоскости и прямой равны, то плоскость и прямая, вырожденные, в точки совпадают.

2. Определение видимости отрезка

Для определения видимости точки сориентируем плоскость так, чтобы её нормаль была направлена в сторону наблюдателя, для этого после определения коэффициентов плоскости подставим в это уравнение координаты наблюдателя. Если соответствующее скалярное произведение будет положительным, то нормаль «смотрит» на наблюдателя.

Если же скалярное произведение будет отрицательно, то необходимо умножить полученные коэффициенты на -1, (перенаправить плоскость в сторону наблюдателя).

Рассмотрим вопрос видимости прямой.

Точка прямой является видимой если скалярное произведение ее координат на коэффициенты плоскости больше нуля. Соответственно точка является невидимой если меньше нуля. Если две точки прямой имеют одновременно скалярное произведение разных знаков, то в этом случае прямая будет видима до точки пересечения с плоскостью и невидима после точки пересечения. Скалярное произведение координат точки на коэффициенты плоскости

Если обе точки имеют положительное скалярное произведение на коэффициенты плоскости, то прямая лежит перед плоскостью и ,соответственно, является полностью видимой.

Аналогично если обе точки имеют отрицательное скалярное произведение, то прямая лежит за плоскостью и является полностью невидимой.

Когда плоскость является проецирующей ([Camera][A]=0) вся прямая будет видимой .

3. Проецирование

Алгоритм проецирования был подробно описан в предыдущей лабораторной работе.

4. Прорисовка

Методы прочерчивания прямых точек и т.д. подробно рассматривались в предыдущих лабораторных работах.

5. Примечание

При определении точки пересечения и визуализации сравнения у нас производятся с нулем. С точки зрения аналитического решения поставленной задачи это правильно. Но из-за погрешности растровой сущности экрана результат аналитического решения может отличаться от того, что наблюдатель будет видеть на экране. Поэтому при реализации программы необходимо ввести некоторую погрешность Eи сравнения производить с ней, а не с нулем.