
- •Сила тяжести:
- •Сила упругости:
- •Сила трения:
- •4 Вида взаимодействий в природе:
- •6. Работа, энергия и мощность силы в поступательном и вращательном движениях. Кинетическая энергия и работа сил.
- •1.Работа и работа сил
- •7. Консервативные и диссипативные сила. Потенциальное поле. Потенциальная энергия упругой силы. Работа по растяжению и сжатию пружины.
- •1.Консервативная и Диссипативная сила. Потенциальное поле.
- •2.Потенциальная энергия упругой силы и работа по растяжению и сжатию пружины.
- •8. Консервативные и диссипативные силы. Потенциальное поле. Потенциальная энергия гравитационной силы. Работа по поднятию тела.
- •1.Консервативная и Диссипативная сила. Потенциальное поле.
- •9.Полная механическая энергия. Закон сохранения механической энергии. Работа в замкнутой системе и работа под действием внешних сил.
- •10)Момент инерции материальной токи, системы и твёрдого тела. Формулы расчета моментов инерции разных симметричных тел. Теорема штейнера.
- •11)Момент силы. Основное уравнение динамики вращающегося твёрдого тела. Условия равновесия твёрдого тела.
- •12)Кинетическая энергия вращающегося твердого тела, закреплённого в точке. Процессия. Гироскопы.
- •13.Скатывание с горки 2ух цилиндров, пустого и сплошного.
- •14.Кинематическое описание движения жидкости. Уравнение движения и равновесия жидкости. Идеальная жидкость.
- •15.Стационарное течение идеальной жидкости. Уравнение Бернулли.
- •16.Вязкая жидкость. Формула Стокса. Турбулентное и ламинарное течение. Число Рейнольдса.
- •17.Поверхностная энергия и натяжение. Капиллярные явления. Поверхностная энергия
- •18.Гармонические колебания и их характеристики. Скорость и ускорение гармонических колебаний. Энергия гармонический колебаний. Способы графического представления колебаний.
- •Сложение взаимно перпендикулярных колебаний
- •20)Гармонический осциллятор. Собственные колебания математического, физического и пружинного маятника
- •21)Гармонический осциллятор. Затухающие колебания и их характеристики.
- •22) Гармонический осциллятор. Вынужденные колебания, дифференциальное уравнение вынужденных колебаний и его решение. Резонанс.
- •23) Волны в упругой среде. Поперечные и продольные волны. Уравнение волны и основные характеристики.
- •24) Стоячие волны. Амплитуда стоячей волны. Узлы и пучности. Длина стоячей волны.
- •26. Теплоемкость. Применение первого начала к изопроцессам: изобарный. Изохорный, изотермический.
- •27. Применение первого начала к изопроцессам: адиабатический процесс.
- •28. Второе начало термодинамики и его применение к тому, что теплота всегда переходит от более нагретого тела к менее нагретому.
- •29. Тепловые двигатели и холодильные машины. Паровой двигатель, двигатель внутреннего сгорания, турбина холодильник.
- •32.Эффект Джоуля-Томпсона. Сжижение газов. Фазовые переходы первого и второго родов.
- •§ 65. Сжижение газов
- •Фазовые переходы I и п рода
11)Момент силы. Основное уравнение динамики вращающегося твёрдого тела. Условия равновесия твёрдого тела.
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 25):
![]()
Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
![]()
где — угол между r и F; r sin = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.
Моментом силы относительно неподвижной оси z называется скалярная величина Mz , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента Мz не зависит от выбора положения точки О на оси z.
Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

выражение для работы при вращении тела:
Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, — угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d точка приложения В проходит путь ds=rd и работа равна произведению проекции силы на направление смещения на величину смещения:
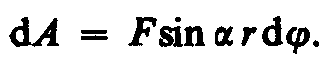
можем записать
![]()
где Frsin = Fl =Mz — момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа
при вращении тела идет на увеличение
его кинетической энергии: dA=dT,
но
 поэтому Mzd
= Jzd,
или
поэтому Mzd
= Jzd,
или
Учитывая,
что получаем
получаем
 (18.3)
(18.3)
Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Можно показать, что если ось z совпадает с главной осью инерции (см. § 20), проходящей через центр масс, то имеет место векторное равенство
 (18.4)
(18.4)
где J — главный момент инерции тела (момент инерции относительно главной оси).
12)Кинетическая энергия вращающегося твердого тела, закреплённого в точке. Процессия. Гироскопы.
абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т1, т2 ,..., тn , находящиеся на расстоянии r1, r2,..., rn от оси.
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri, и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
![]() (17.1)
(17.1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:

или

Используя выражение (17.1), получаем

где Jz — момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
 (17.2)
(17.2)
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv2/2), следует, что момент инерции — мера инертности тела при вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

где m — масса катящегося тела; vc — скорость центра масс тела; Jc — момент инерции тела относительно оси, проходящей через его центр масс; — угловая скорость тела.

Гироско́п (от др.-греч. γῦρος «круг» и σκοπέω «смотрю») — устройство, способное реагировать на изменение углов ориентации связанного с ним тела относительно инерциальной системы координат, как правило, основанное на законе сохранения вращательного момента (момента импульса)
поведение гироскопа описывается уравнением:
![]()
где векторы
![]() и
и
![]() являются,
соответственно, моментом
силы, действующей на гироскоп, и его
моментом
импульса, скаляр
являются,
соответственно, моментом
силы, действующей на гироскоп, и его
моментом
импульса, скаляр
![]() —
его моментом
инерции, векторы
—
его моментом
инерции, векторы
![]() и
и
![]() угловой
скоростью и угловым
ускорением.
угловой
скоростью и угловым
ускорением.
Отсюда следует, что
момент
силы
,
приложенный перпендикулярно оси вращения
гироскопа, то есть перпендикулярный
,
приводит к движению, перпендикулярному
как
,
так и
,
то есть к явлению прецессии.
Угловая скорость прецессии
![]() гироскопа
определяется его моментом импульса и
моментом приложенной силы[10]:
гироскопа
определяется его моментом импульса и
моментом приложенной силы[10]:
![]()
то есть обратно пропорциональна скорости вращения гироскопа.
Прецессия гироскопа
Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы.
Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
