9.Полная механическая энергия. Закон сохранения механической энергии. Работа в замкнутой системе и работа под действием внешних сил.

1. Полная механическая энергия. Закон сохранения механической энергии.

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:

Е = Е_к + Е_п.

Закон сохранения механической энергии: механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.

_2.Работа в замкнутой системе и работа под действием внешних сил.

Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют. В этой системе работа равна нулю.

Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил :

Авн = ΔЕ = Е – Е0, (20)

где Е и Е0 – полные механические энергии системы в конечном и начальном состояниях соответственно.

10)Момент инерции материальной токи, системы и твёрдого тела. Формулы расчета моментов инерции разных симметричных тел. Теорема штейнера.

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс л материальных точек системы на квадраты их расстояний до рассматриваемой оси:

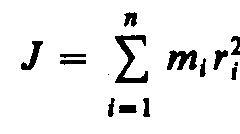
В случае непрерывного распределения масс эта сумма сводится к интегралу

где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.

момент инерции сплошного цилиндра

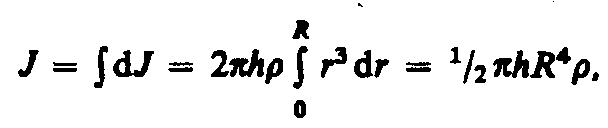
но так как R²h — объем цилиндра, то его масса m=R²h, а момент инерции

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:

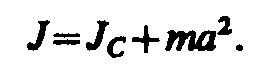
В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т — масса тела).

Таблица 1

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Если  — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии от неё, равен

,

где  — полная масса тела.