3. Формула Грина.

Формула Грина связывает двойной интеграл по плоской области с криволинейным интегралом по контуру этой области. Пусть функции P(x,y), Q(x,y), P'y(х,у), Q'x(х,у) непрерывны в замкнутой области D, ограниченной контуром L. Пусть контур L, кроме того, пересекается прямыми, параллельными осям координат, не более чем в двух точках. Пусть уравнение АСВ есть y = y1(x) при a ≤ x ≤ b , и уравнение АКВ есть y = y2(x) при a ≤ x ≤ b. Преобразуем двойной интеграл:

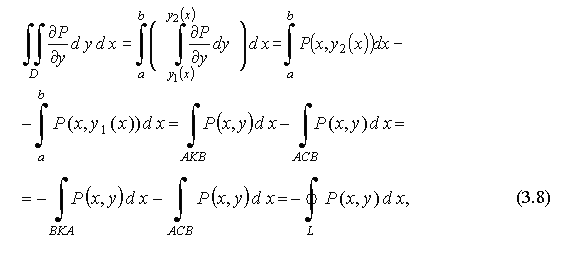
здесь символ означает криволинейный интеграл по замкнутому контуру L. Аналогично получается Вычитая из формулы (3.9) формулу (3.8), получаем формулу Грина В формулах направление обхода контура - положительное (против часовой стрелки), т. е. область D при движении по контуру L всё время остается слева. С помощью формулы Грина можно получить выражения площади плоской фигуры через криволинейный интеграл по контуру этой фигуры. Для этого достаточно подобрать P(x,y) и Q(х,y) такими, чтобы в области D выполнялось условие тогда двойной интеграл в формуле будет давать величину S площади области D.

4. Поток, ф-ла Гаусса-Остроградского.

Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность. Пусть поверхность S расположена в поле скоростей частиц несжимаемой жидкости с плотностью ρ = 1. Можно показать, что поток векторного поля в этом случае равен где – единичный нормальный вектор к поверхности S, расположенный по одну сторону с вектором , а величина . Независимо от физического смысла вектора интеграл по поверхности называют потоком векторного поля через поверхность S.Пусть и тогда поток П вектора через поверхность S можно записать в виде: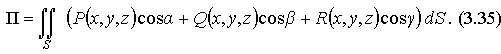 Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах: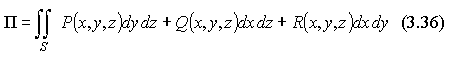 Рассмотрим пространственную область V. Снизу эта область ограничена поверхностью S1 с уравнением: z = h (x, y); сверху – поверхностью S2 с уравнением: z = H (x, y); сбоку – цилиндрической поверхностью S3 с образующими, параллельными оси Oz. Пусть функция R(x, y, z) и её частная производная (x, y, z) непрерывны в области V, τ – проекция области V на Oxy. Рассмотрим тройной интеграл: Здесь поверхностные интегралы вычисляются по сторонам поверхностей S1 и S2, "внешним" по отношению к телу V. Если учесть, что: (потому, что нормаль к этой цилиндрической поверхности составляет с осью Оz угол 90°), то получаем: где интегрирование выполняется по внешней стороне поверхности S, ограничивающей тело V.Аналогично получаем: Складывая формулы получаем формулу Остроградского:

То есть формула Остроградского выражает поверхностный интеграл общего вида по внешней стороне замкнутой поверхности S через тройной интеграл по области V, ограниченной этой поверхностью. Дивергенцией или расходимостью векторного поля называется скалярная функция, определяемая равенством: На этот раз векторное поле порождает скалярное поле div . С учетом понятий дивергенции и потока векторного поля формулу Остроградского можно представить в форме: т. е. поток векторного поля через замкнутую поверхность S в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.