Б илет №7. Применение общего уравнения динамики для силового расчета механизмов (одноподвижных и многоподвижных). Пример с рычажным механизмом.

Д ля любой системы материальных точек с идеальными связями сумма работ всех активных сил и всех сил инерции на любом возможном перемещении в любой фиксированный момент времени равна нулю. Это положение записывается в аналит. форме: (4.25)

и называется уравнением Даламбера-Лагранжа или общим уравнением динамики. В уравнении (4.25) и – активная сила и сила инерции к-й материальной точки, – ее возможное перемещение, М – число мат. точек в системе.

Рассмотрим звено механизма, являющееся абсолютно твердым телом. (рис.4.10). Для произвольной точки звена имеем

(4.26) где – возможное перемещение полюса 0, – вектор бесконечно малого поворота, – радиус-вектор к-й точки. Подставив (4.26) в (4.25), находим

(4.27)

Здесь Р и Ф – главные векторы, а 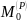и – главные моменты активных сил и сил инерции звенa. Складывая выражения (4.27) для всех подвижных звеньев (4.28) где N – число подвижных звеньев.

Если механизм имеет w степеней свободы и q₁,…,q_w – его обобщенные координаты, то

(4.29)

(4.29) в (4.28) (4.30)

выражение не частная производная, а отношение бесконечно малых

Для механизма с одной степенью подвижности (4.31)

(4.32)

Отсюда следует, что сумма возможных мощностей всех активных сил и сил инерции в любой момент времени равна нулю для механизма с одной степенью подвижности при идеальных кинематических парах.

Уравнение Даламбера-Лагранжа в форме (4.28) удобно использовать для определения обобщенных движущих сил. (4.33)

(4.34)

Рассмотрим в качестве примера задачу об определении движущей силы для рычажного механизма, показанного на рис.4.4. Поскольку в плоском механизме векторы возможных перемещений всех точек параллельны плоскости движения, а векторы малых поворотов звеньев перпендикулярны ей, для составления уравнений Даламбера-Лагранжа достаточно определить компоненты активных сил и сил инерции, лежащие в плоскости движения, и компоненты моментов, ей перпендикулярные. Остальные компоненты сил и моментов не совершают работы на возможном перемещении плоского механизма, и не влияют на величины движущих сил. (4.36)где ₂ – абсолютный угол поворота звена.

Б илет №8. Применение общего уравнения динамики для определения реакции в кинематической паре.

Общее уравнение динамики позволяет определить реакции всех освобождающих связей. для механизма на рис.4.4 определим R₀₃ в поступательной паре. Освободим связь, соответствующую этой реакции; условную доп. степень подвижности(перемещение вдоль y) Тогда получим механизм с двумя степенями подвижности, в котором координата y_B будет играть роль второй входной координаты, а реакция R₀₃ станет обобщенной «движущей» силой, соответствующей этой координате.Применим к этому механизму общее уравнение динамики в форме для силы R₀₃

(4.37)

Отметим, что силы и моменты сил инерции, входящие в это выражение, должны определяться при заданных значениях и при y_B = 0, = 0, т.е. они должны вычисляться для заданного движения исследуемого механизма без какого-либо учета дополнительной подвижности. Выражение (4.37) получено из условия равенства нулю работ активных сил и сил инерции на возможном перемещении, соответствующем q = 0, y_B  0. работу будут совершать только силы, приложенные к звеньям 2 и 3. При этом из уравнения (4.37) получим (4.38)Из геом. соображений (см. рис.4.11) (4.39)Подставив (4.39) в (4.38), находим величину R₀₃ в заданном положении.