Воспользуемся функцией

При t = 1 получим: (1+1)¹⁴=

В нашем случае в группу не может входить 0 человек, поэтому:

-искомое число способов.

=2¹⁴ =1 С помощью производящей функции мы можем получать как сами комбинатор объекта (сочетание, перестановка и т. п.).

Чтобы получить интересующие нас объекты, состоящие из k элементов, нужно выписать коэффициент ряда при t^k. По слагаемым, присутствующим в a_k, определяются нужные объекты.

Очень часто производящая функция строится так, что в ее представлении присутствуют формами обозначения элементов, образующих комбинаторы объекты x₁,x₂,…,x_n.

Сколько слагаемых в коэффициенте, столько и объектов.

Чтобы подсчитать количество объектов длин k, нужно вычислить коэффициент a_k, положив x₁=x₂=x₃=…=x_n=1 соответствующий полином:

Д

m_i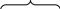

ействительно,

хi отсутствует в сочетании

хi присутствует 1 раз

присутствует 2 раза

присутствует mi раз

С учетом сказанного, для всех n видов элементов производящая функции имеет вид:

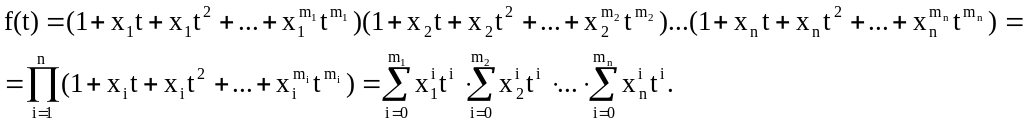
Положив x₁=x₂=x₃=…=x_n=1, получим производящую функцию для числа сочетаний из n по k с ограниченным числом повторений элементов

З

n=3

m₁=2, m₂=2, m₃=3

адача. Дано х₁, х₁, х₂, х₂, х₃

2 элемента вида х1

2 элемента вида х2

1 элемент вида х3

Требуется получить сочетание из данных элементов по 3 и рассчитать их количество.

F (t)=(1+x₁t+x₁²t²)(1+x₂t+x₂²t²)(1+x₃t)=[выпишем коэффициент при t³, т.к. к=3]+1t⁰+(…)t²+(x₁x₂x₃+ x₂²x₁⁴+x₁²x₃+x₁²x₃+x₂²x₃)t³+(…)t⁴+(…)t⁵=

x1 - 1раз x2 - 1раз x3 - 1раз

x1 - 2раз x2 - 1раз x3 - 0раз

Коэффициент при t³ a³=x₁x₂x₃+x₁x₁x₂+x₁x₁x₃+x₂x₂x₁+x₂x₂x₃..

Слагаемое - это все возможные сочетания из имеющихся элементов по 3.

Число таких сочетаний вычисляем, положив a₃=1+1+1+1+1=5.

3. Производящая функция для числа сочетаний из n элементов по k с неограниченным числом повторений элементов.

Имеем элементы n видов – вида x₁, вида x₂,…, вида x_n.

Из этих элементов набираем сочетания, элемент х₂ может появляться в сочетании любое количество раз.

По аналогии с предыдущей задачей построим функцию:

F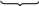 *(t)=(1+t+t²+…)(1+t+t²+…)…(1+t+t²+…)=(1+t+t²+…)ⁿ=( )ⁿ=(1+(-t))^-n=

этот ряд сходится к функции

= = = == = =

этот результат был получен ранее

Если комбинаторными объектами являются перестановки, то производящая функция позволит только подсчитать их число. Сами объекты получить не сможем.

4. Производящая функция для числа перестановок длины k из n различных элементов.

Из элементов x₁,x₂,…,x_n строим перестановки длины k. Заметим, что каждому сочетанию из k различных элементов соответствует k! перестановок из этих элементов.

У нас есть производящая функция для числа сочетаний из n по k различных элементов: .

Значит, функция является производящей для перестановок длины k из n различных элементов.

Задача. Найти число перестановок длины 2 и длины 3 из элементов x₁,x₂,x₃,x₄.

Запишем производящую функцию и найдем коэффициент при t² и t³:

действительно имеет 6 х₁х₂ х₁х₃ х₁х₄ х₂х₃ х₂х₄ х₃х₄

состояний и 12 перестановок х₂х₁ х₃х₁ х₄х₁ х₁х₂ х₄х₂ х₄х₃

5. Производящая функция для числа перестановок длины k из n видов элементов. Элементы могут повторяться, число повторений ограничено.

Воспользуемся соответствующей производящей функцией для сочетаний с повторениями элементов:

Если бы элементы не повторялись, то в каждом сочетании длины k мы могли бы переставлять элементы k! способами, каждый раз получая при этом новую перестановку.

Но так как в сочетании могу оказаться одинаковые элементы, то разных перестановок будет меньше.

Подсчитаем во сколько раз.

x_i элемент может встретиться в сочетании либо m_i раз, тогда мы можем переставить его m_i! способами, и перестановка не измениться,

либо m_i-1 раз - перестановка его (m_i-1)! способами не изменит объект и так далее.