19. Циклы.Цикл Карно и его коэф полезного действия. Термодинамическая шкала температур.

Цикл-наз процесс,при кот система,пройдя через ряд состояний,возр в исхизобр в виде замкнутой кривой.цикл,сов идеал газом можно разбить на процесс расширения и сжатия. прямой(если за цикл сов пол -протек по час стрелке),так и в обратный(если сов отр -цикл протек против час стрелки).

Цикл Карно- идеал термодинамич цикл.Тепл машина Карно,работ по этому циклу, облад макс КПД из всех машин,у кот макс и мин темпер осуществл цикла совпад соответс с макс и мин темпер цикла Карно.Состоит из 2 адиабатических и 2 изотермических процессов.Одним из важных св-в цикла Карно явл его обратимость:он может быть провед как в прямом,как и в обратн направ,при этом энтропия адиабатически изолированной(без теплообмена с окр средой) системы не меняется. Цикл Карно состоит из четырёх стадий:1.Изотермическое расшир (на рис — процесс A→Б). В начале процесса раб тело имеет темп T_Н,то есть темп нагрев.Затем тело прив в контакт с нагревателем,кот изотермически(при пост темпер)передему кол-во теплоты Q_Н.При этом объём рабочего тела ↑.2.Адиабатическое(изоэнтропическое)расшир (на рис процесс Б→В).Раб тело отсоед от нагрев и продол расшир без теплообм с окрй средой.При этом его темпер ↓до темпер холодильника.3.Изотермическое сжатие(на рис процесс В→Г).Раб тело, имеющ к тому врем темпер T_х, прив в контакт с холодил и начинает изотермически сжиматься,отдавая холодильнику кол-во теплоты Q_х.4.Адиабатическое(изоэнтропическое)сжатие (на рис процесс Г→А).Рабтело отсоед от холодил и сжим без теплообм с окр средой.При этом его темпер ↑ до темпер нагревателя. При изотерм процессах темпер остаётся постоянной,при адиабат отсут теплообм,а значит, сохраняется энтропия: при .Поэтому цикл Карно удобно предст в координатах T и S.

КПД тепловой машины Карно:Кол-во теплоты,пол раб телом от нагрев при изотермич расшир, равно .При изотермич сжатии рабтело отдало холодил Отсюда коэффициент полезного действия Карно:

Из посл выраж видно,что КПД тепловой машины Карно зав только от Т нагр-ля и хол-ка, КПД может состав 100 % только в том случае,если Т хол-ка равна 0.Это невозможно,но не из-за недостиж абс нуля,а из-за того,что такой цикл или нельзя замкнуть, или он вырожд в совок 2-х совпад адиабат и изотерм.Поэтому макс КПД любой тепловой машины будет < или = КПД тепловой машины Карно,раб при тех же Т нагр-ля и хол-ка.

Термодинамическая шкала температур (Кельвина шкала) - абсол шкала темпер,не зав от св-в термометр в-ва(начало отсчета - абсолютный нуль температуры).Постр термодинам температ шкалы основано на втором начале термодинамики и,в частности,на независ кпд Карно цикла от природы рабтела.Единица термодин темп - кельвин (К) - определяется как 1/273,16 часть термод темпер тройной точки воды.

20.Приведенная теплота. Энтропия. Математическая формулировка 2 начала термодинамики.

Приведенная теплота-Из цикла Карно видно,что = между собой отнош Q к Т,при кот они были пол или отданы в изотермическом процессе:

Отнош теплоты Q в изотермическом процессе Т,при кот происх передача Q, называется приведенной теплотой : Для подсчета приведенной теплоты в произвольном процессе необх разбить этот процесс на бесконечно малые участки, где Т можно считать константой. Приведенная теплота на таком участке будет равна .Суммируя на всех участках процесса, получим:

Тогда в обратимом цикле Карно имеем:

Этот результат справедлив для любого обратимого процесса.Таким образом, для процесса, происх по замкнутому циклу

Из рав-ва нулю интеграла,взятого по замкн контуру,следует, что подынтегр выр есть полный дифференциал некот фу-и,кот опред только состоян системы и не зав от пути, каким система пришла в это состояние.Это позвол ввести новую фу-ю состояния S:

Ф-ия состояния,полный дифференциал кот равен , наз энтропией– мера способности теплоты превращаться в другие виды энергии.        Энтропия S – это отнош пол или отданной Q к Т, при кот происх этот процесс.Пон S впервые введено Р. Клаузиусом в 1854 г. Энтропия-функция состояния,диф которого явл ∂Q/T. Для обр процессов:∂S=0, необрат цикл:∂S>0 это только для замкн системы,если же система обменивается теплотой с внеш средой,то ее S может вести себя любым образом. Соотн формул можно предст в виде неравенства Кл-са:∂S≥0,т.е. S замкн системы может либо возр(необр процесс),либо конст(обратн процесс).

Если система сов равновесный переход из сост 1 в2,то: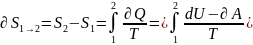 ,опр S лишь с точностью до аддитивной постоянной.физ смысл имеет не сама S,а разность ее.найдем изм в процессах идеал газа,т.к. ,то или ,т.е.изм S идел газа при переходе из 1 в2 не зав от вида процесса перехода 1→2.т.к. для адиаб процесса и S-const,т.е. адиаб обрат процесс протек при пост S-изоэнтропический процесс. при изотерм процессе Т1=Т2: , при изохорном процессе V1=V2: . Обладает св-вом аддитивности:энтр системы =сумме энтр тел,вход в систему.

Математическая формулировка 2 начала термодинамики: