
- •18.Обратимые и необратимые процессы.Неравноценность теплоты и работы.Второе начало термодинамики.
- •19. Циклы.Цикл Карно и его коэф полезного действия. Термодинамическая шкала температур.
- •20.Приведенная теплота. Энтропия. Математическая формулировка 2 начала термодинамики.
- •21. Макросистемы. Понятие о вероятности. Функция распределения.
- •22. Функции распределения молекул по скоростям. Распр Максвелла и его анализ.
- •23. Скорости газовых мол. Внутренняя энергия идеал газа.
- •24. Распределение Больцмана. Распр Максвелла-Больцмана.
МКТ
11. Основные положения молекулярно-кинетической теории, основное уравнение молекулярно-кинетической теории:
В основе молекулярно-кинетической теории строения вещества лежат три положения:
все тела состоят из частиц (атомов, молекул, ионов и др.);
частицы непрерывно хаотически движутся;
Частицы взаимодействуют друг с другом.
Первое положение
подтверждают испарение жидкостей и
твердых тел, получение фотографий
отдельных крупных молекул и групп
атомов, косвенные измерения масс и
размеров молекул. Второе положение
подтверждают такие явления, как
броуновское движение и диффузия.
Броуновское движение - беспорядочное
движение малых частиц в жидкости или
газе, происходящее под действием молекул
окружающей среды. Причина броуновского
движения - тепловое движение молекул
среды и отсутствие точной компенсации
ударов, испытываемых частицей со стороны
окружающих ее молекул. Удары молекул
среды приводят частицу в беспорядочное
движение: скорость ее меняется по
величине и направлению. Диффузия имеет
место в газах, жидкостях и твердых телах.
Наиболее быстро диффузия происходит в
газах, медленнее - в жидкостях, еще
медленнее - в твердых телах. Скорость
диффузии определяется характером
теплового движения частиц в этих средах.
Подтверждением третьего положения
является возникновение упругих сил при
деформациях тел, существование различных
агрегатных состояний (твердого, жидкого,
газообразного) одного и того же
вещества.Вывод основного уравнения
МКТ: Пусть имеется кубический сосуд с
ребром длиной
 и
одна частица массой
и
одна частица массой
 в нём. Обозначим скорость движения
в нём. Обозначим скорость движения
 ,
тогда перед столкновением со стенкой
сосуда импульс частицы равен
,
тогда перед столкновением со стенкой
сосуда импульс частицы равен
 ,
а после
,
а после
 ,
поэтому стенке передается импульс
,
поэтому стенке передается импульс
 Время, через которое частица сталкивается
с одной и той же стенкой, равно
Время, через которое частица сталкивается
с одной и той же стенкой, равно
 Отсюда следует:
Отсюда следует:
 Так как давление
Так как давление
 ,
следовательно сила
,
следовательно сила
 Подставив, получим:
Подставив, получим:
 Преобразовав:
Преобразовав:
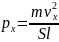 Так как рассматривается кубический
сосуд
Так как рассматривается кубический
сосуд
 ,
то
,
то
 Соответственно,
Соответственно,
 и
и
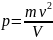 Таким образом, для большого числа частиц
верно следующее:
Таким образом, для большого числа частиц
верно следующее:
 , аналогично для осей y и z. Поскольку ,
, аналогично для осей y и z. Поскольку ,
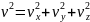 , то
, то
 .
Это следует из того, что все направления
движения молекул в хаотичной среде
равновероятны. Отсюда
.
Это следует из того, что все направления
движения молекул в хаотичной среде
равновероятны. Отсюда
 или
или
 Пусть
Пусть
 —
среднее значение кинетической энергии
всех молекул, тогда:
—
среднее значение кинетической энергии
всех молекул, тогда:
 ,
откуда
,
откуда
 Для одного моля выражение примет вид
Для одного моля выражение примет вид
 .
.
12. Термодинамические параметры. Уравнение состояния идеального газа:
Термодинамической
системой называется совокупность
макроскопических тел, которые могут
обмениваться энергией между собой и с
внешней средой (т.е. с другими телами).
Термодинамическая система может
находиться в различных состояниях,
отличающихся температурой, давлением,
объёмом, плотностью и т.д. Подобные
величины, характеризующие состояние
системы, называют параметрами состояния.
Состояние т-д системы будет равновесным,
если все параметры имеют определенные
значения, не изменяющиеся с течением
времени. Т-д системы, которые не
обмениваются с внешней средой ни
энергией, ни веществом – изолированные
(замкнутые). Процесс релаксации – переход
системы, находящейся в неравновесном
состоянии, в равновесной состояние
после ее изоляции. Термодинамический
процесс – переход системы их одного
состояния в другое. Равновесный
(квазистатический) процесс – бесконечно
медленный процесс, состоящий из
последовательности равновесных
состояний. Все равновесные процессы
обратимые. Круговой процесс (цикл) –
процесс, при котором система после ряда
изменений возвращается в исходное
состояние. Параметры состояние закономерно
связаны друг с другом. Соотношение,
определяющее связь между параметрами
состояния какого-либо тела, называется
уравнением состояния этого тела. В
простейшем случае равновесное состояние
тела определяется температурой, объемом
и давлением. Связь между ними выражает
формула:
 – уравнение состояния тела. При обычных
условиях (комнатной температуре и
атмосферном давлении):
– уравнение состояния тела. При обычных
условиях (комнатной температуре и
атмосферном давлении):
 - уравнение состояния идеального газа
- газа, взаимодействием между молекулами
которого можно пренебречь. Согласно
закону Авогадро, при нормальных условиях
(
- уравнение состояния идеального газа
- газа, взаимодействием между молекулами
которого можно пренебречь. Согласно
закону Авогадро, при нормальных условиях
( ),
объём моля любого газа равен 22,4 моль/л.
Когда количество газа равно 1 молю,
- одинаковая константа для всех газов,
обозначим ее R, тогда
),
объём моля любого газа равен 22,4 моль/л.
Когда количество газа равно 1 молю,
- одинаковая константа для всех газов,
обозначим ее R, тогда
 (
( -
- ).
).
 – газовая постоянная.
– газовая постоянная.
 (M – молярная масса газа).
При одинаковых p и T
газ массы m занимает объем
V, в m/M
больший, чем
Поэтому:
(M – молярная масса газа).
При одинаковых p и T
газ массы m занимает объем
V, в m/M
больший, чем
Поэтому:
 .
.
 , где
, где
 - число модекул, содержащихся в массе m
газа.
- число модекул, содержащихся в массе m
газа.
 - постоянная Больцмана (доля газовой
постоянной, приходящаяся на одну
молекулу). Так:
- постоянная Больцмана (доля газовой
постоянной, приходящаяся на одну
молекулу). Так:
 .
.
 - число молекул в единице объема газа,
Следовательно:
- число молекул в единице объема газа,
Следовательно:
 .
Уравнения
,
,
– различные формы записи уравнения
состояния идеального газа.
.
Уравнения
,
,
– различные формы записи уравнения
состояния идеального газа.
13. Первое начало термодинамики. Понятие функции состояния. Работа расширения
Внутренняя энергия
какого-либо тела слагается из кинетической
энергии поступательного и вращательного
движения молекул, кинетической и
потенциальной энергией колебательного
движения атомов в молекулах, потенциальной
энергией взаимодействия между молекулами
и внутримолекулярной энергией. Изменение
внутренней энергии может происходить
за счет совершения над телом работы
 и передачи ему теплоты
и передачи ему теплоты
 .
- работа, совершаемая внешними телами
над данным телом,
.
- работа, совершаемая внешними телами
над данным телом,
 - работа, совершаемая данным телом над
внешними телами.
- количество теплоты, переданное данному
телу внешней средой,
- работа, совершаемая данным телом над
внешними телами.
- количество теплоты, переданное данному
телу внешней средой,
 - количество теплоты, переданное данным
телом внешней среде. При совершении
одним телом работы A над
другим, равно как и при сообщении одним
телом другому теплоты
эти тела обмениваются внутренней
энергией: энергия одного увеличивается,
другого - уменьшается. Это следует из
закона сохранения энергии. В Термодинамике
этот закон – первое начало (количество
теплоты, сообщенное системе, идет на
приращение внутренней энергии системы
и на совершение системой работы над
внешними телами):
- количество теплоты, переданное данным
телом внешней среде. При совершении
одним телом работы A над
другим, равно как и при сообщении одним
телом другому теплоты
эти тела обмениваются внутренней
энергией: энергия одного увеличивается,
другого - уменьшается. Это следует из
закона сохранения энергии. В Термодинамике
этот закон – первое начало (количество
теплоты, сообщенное системе, идет на
приращение внутренней энергии системы
и на совершение системой работы над
внешними телами):
 где
где
 – начальное и конечное значения
внутренней энергии. Внутренняя энергия
является функцией состояния системы.
Поэтому ее приращение при переходе
системы из одного состояния в другое
не зависит от пути, по которому совершался
переход. Формула работы расширения:
– начальное и конечное значения
внутренней энергии. Внутренняя энергия
является функцией состояния системы.
Поэтому ее приращение при переходе
системы из одного состояния в другое
не зависит от пути, по которому совершался
переход. Формула работы расширения:
 или
или
 При расширении рассматриваемого тела
приращение объема
При расширении рассматриваемого тела
приращение объема
 положительно, положительна и
положительно, положительна и
 ,
при сжатии обе величины отрицательны.
При сжатии газ совершает отрицательную
работу, а внешние тела, действующие на
газ, - положительную. Работа ,совершаемая
при конечных изменениях объема,
вычисляется путем суммирования
элементарных работ, т.е. путем
интегрирования:
,
при сжатии обе величины отрицательны.
При сжатии газ совершает отрицательную
работу, а внешние тела, действующие на
газ, - положительную. Работа ,совершаемая
при конечных изменениях объема,
вычисляется путем суммирования
элементарных работ, т.е. путем
интегрирования:

14. Внутренняя энергия и теплоёмкость идеального газа
Теплоемкость –
величина, равная количеству теплоты,
которое нужно сообщить телу, чтобы
повысить его температуру на один кельвин:
 =[
=[ ]
Теплоемкость единицы массы вещества –
удельная теплоемкость c
=[
]
Теплоемкость единицы массы вещества –
удельная теплоемкость c
=[ ].
Теплоемкость моля вещества – молярная
C=[
].
Теплоемкость моля вещества – молярная
C=[ ].
].
 , где M – молярная масса.
, где M – молярная масса.
 – теплоемкость при постоянном объеме,
– теплоемкость при постоянном объеме,
 - при постоянном давлении. Если нагревание
происходит при постоянном объеме, тело
не совершает работы над внешними телами,
вся теплота идет на приращение внутренней
энергии
- при постоянном давлении. Если нагревание
происходит при постоянном объеме, тело
не совершает работы над внешними телами,
вся теплота идет на приращение внутренней
энергии
 ,
значит
,
значит

 .
.
 , т.к. почти не зависит от температуры,
поэтому
, т.к. почти не зависит от температуры,
поэтому
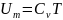 Внутрення я энергия массы газа будет
равна
Внутрення я энергия массы газа будет
равна
 При постоянном давлении нагреваемое
тело расширяется, часть подводимой
теплоты расходуется на совершение
работы над внешними телами.
При постоянном давлении нагреваемое
тело расширяется, часть подводимой
теплоты расходуется на совершение
работы над внешними телами.
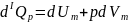 Молярная теплоемкость газа при постоянном
давлении :
Молярная теплоемкость газа при постоянном
давлении :
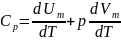 . так как
, то
. так как
, то
 Продифференцировав
Продифференцировав
 по T получим
по T получим
 Работа, совершаемая молем идеального
газа при повышении его температуры на
один кельвин при постоянном давлении,
равна газовой постоянной R.
Отношение
Работа, совершаемая молем идеального
газа при повышении его температуры на
один кельвин при постоянном давлении,
равна газовой постоянной R.
Отношение
 - характерная для каждого газа величина.
- характерная для каждого газа величина.

 . Внутренняя энергия произвольной массы
газа:
. Внутренняя энергия произвольной массы
газа:
 , она пропорциональна произведению
давления на объем.
, она пропорциональна произведению
давления на объем.
15. Изотермический процесс (уравнение состояния, первое начало, работа):
Изотермический процесс
(T=const)
описывается законом Бойля-Мариотта:
для данной массы газа при постоянной
температуре произведение давления газа
на его объем есть величина постоянная:
pV=const при
T=const, m=
const. Диаграмма этого
процесса (изотерма) в координатах p,
V представляет собой
гиперболу, расположенную тем выше, чем
выше температура, при которой происходит
процесс. Работа изотермического
расширения:
 Так как при T=const
внутренняя энергия идеального газа не
изменяется:
Так как при T=const
внутренняя энергия идеального газа не
изменяется:
 , то из первого начала термодинамики
(
, то из первого начала термодинамики
( )
следует, что для изотермического
процесса
)
следует, что для изотермического
процесса
 ,
т.е. все количество теплоты, сообщаемое
газу, расходуется на совершение им
работы против внешних сил:
,
т.е. все количество теплоты, сообщаемое
газу, расходуется на совершение им
работы против внешних сил:
 . Следовательно, для того чтобы при
расширении газа температура не понижалась,
к газу в течение изотермического процесса
необходимо подводить количество теплоты,
эквивалентное внешней работе расширения.
Теплоемкость (dT=0)равна
. Следовательно, для того чтобы при
расширении газа температура не понижалась,
к газу в течение изотермического процесса
необходимо подводить количество теплоты,
эквивалентное внешней работе расширения.
Теплоемкость (dT=0)равна
 ,
постоянна.
,
постоянна.
16. Изобарический и изохорический процессы (уравнение состояния, первое начало, работа)
Для данной массы газа
при постоянном объеме отношение давления
газа к его температуре есть величина
постоянная:
 при
при
 ,
,
 .
Диаграмма изохорного процесса (V=const)
– изохора – в координатах p,
V изображается прямой,
параллельной оси ординат, где увеличение
давления – изохорное нагревание,
уменьшение- изохорное охлаждение. При
изохорном процессе газ не совершает
работы над внешними телами, т.е.
.
Диаграмма изохорного процесса (V=const)
– изохора – в координатах p,
V изображается прямой,
параллельной оси ординат, где увеличение
давления – изохорное нагревание,
уменьшение- изохорное охлаждение. При
изохорном процессе газ не совершает
работы над внешними телами, т.е.
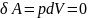 . Из первого начала термодинамики (
)
следует, что вся теплота, сообщаемая
газу, идет на увеличение его внутренней
энергии:
. Из первого начала термодинамики (
)
следует, что вся теплота, сообщаемая
газу, идет на увеличение его внутренней
энергии:
 .
Так как
.
Так как
 , то для произвольной массы газа получим:
, то для произвольной массы газа получим:
 Для данной массы газа при постоянном
давлении отношение объема газа к его
температуре есть величина постоянная:
Для данной массы газа при постоянном
давлении отношение объема газа к его
температуре есть величина постоянная:
 при
при
 ,
,
 .
Диаграмма изобарного процесса (P=const)
– изобара – в координатах p,
V изображается прямой,
параллельной оси V.
Теплоемкость равна
постоянна.
.
Диаграмма изобарного процесса (P=const)
– изобара – в координатах p,
V изображается прямой,
параллельной оси V.
Теплоемкость равна
постоянна.
При изобарном процессе
работа газа при увеличении объема от
 до
до
 равна
равна
 и определяется площадью заштрихованного
прямоугольника. Если использовать
уравнение Менделеева-Клапейрона для
выбранных нами двух состояний, то
и определяется площадью заштрихованного
прямоугольника. Если использовать
уравнение Менделеева-Клапейрона для
выбранных нами двух состояний, то
 ,
,
 , откуда
, откуда
 . Тогда выражение работы изобарного
расширения примет вид:
. Тогда выражение работы изобарного
расширения примет вид:
 Отсюда вытекает физический смысл
молярной газовой постоянной R:
если
Отсюда вытекает физический смысл
молярной газовой постоянной R:
если
 ,
то для газа R=A,
т.е. R численно равна работе
изобарного расширения 1 моль идеального
газа при нагревании его на 1 К. В изобарном
процессе при сообщении газу массой m
количества теплоты
,
то для газа R=A,
т.е. R численно равна работе
изобарного расширения 1 моль идеального
газа при нагревании его на 1 К. В изобарном
процессе при сообщении газу массой m
количества теплоты
 его внутренняя энергия возрастает на
величину
его внутренняя энергия возрастает на
величину
 согласно
При этом газ совершает работу
Теплоемкость равна
постоянна
согласно
При этом газ совершает работу
Теплоемкость равна
постоянна
17. Адиабатный процесс (уравнение состояния, первое начало, работа)
Адиабатный процесс
- процесс, при котором отсутствует
теплообмен
 между системой и окружающей средой. К
адиабатическим процессам можно отнести
быстропротекающие процессы. Из первого
начала термодинамики
следует, что
между системой и окружающей средой. К
адиабатическим процессам можно отнести
быстропротекающие процессы. Из первого
начала термодинамики
следует, что
 ,
т.е. внешняя работа совершается за счет
изменения внутренней энергии системы.
Так как
,
т.е. внешняя работа совершается за счет
изменения внутренней энергии системы.
Так как
 ,
, для произвольной массы газа
,
, для произвольной массы газа
 Продифференцировав
получим
Продифференцировав
получим
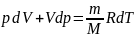 .
Исключив T , получаем
.
Исключив T , получаем
 . Так как
. Так как
 ,
найдем
,
найдем
 . Интегрируя в переделах от
. Интегрируя в переделах от
 до
до
 и соответственно
и соответственно
 получим
получим
 или
или
 . Так как состояния 1, 2 выбраны произвольно,
можно записать
. Так как состояния 1, 2 выбраны произвольно,
можно записать
 .
Полученное выражение есть уравнение
адибатического процесса, называемое
также уравнением Пуассона. Переходя к
переменным T, V
или p,T
получаем
.
Полученное выражение есть уравнение
адибатического процесса, называемое
также уравнением Пуассона. Переходя к
переменным T, V
или p,T
получаем
 ,
,
 .
Последние три – выражения адиабатического
процесса. Величина
.
Последние три – выражения адиабатического
процесса. Величина
 показатель адиабаты (коэффициент
Пуассона). Диаграмма адиабатного процесса
в координатах
показатель адиабаты (коэффициент
Пуассона). Диаграмма адиабатного процесса
в координатах
 изображается гиперболой. При адиабатическом
сжатии (увеличение давления) увеличение
давления газа обусловлено не только
уменьшением его объема, как при
изотермическом сжатии, но и повышением
температуры. Работа, совершаемая газом:
изображается гиперболой. При адиабатическом
сжатии (увеличение давления) увеличение
давления газа обусловлено не только
уменьшением его объема, как при
изотермическом сжатии, но и повышением
температуры. Работа, совершаемая газом:
 Если газ адиабатически расширяется от
объема
до
,
его температура уменьшается от
Если газ адиабатически расширяется от
объема
до
,
его температура уменьшается от
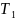 до
до
 и работа расширения идеального газа
и работа расширения идеального газа
 Можно преобразовать к виду
Можно преобразовать к виду
 где
где
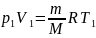 .
Работа, совершаемая газом при адиабатическом
расширении меньше, чем при изотермическом,
т.к. происходит охлаждение газа.
Теплоемкость равна
.
Работа, совершаемая газом при адиабатическом
расширении меньше, чем при изотермическом,
т.к. происходит охлаждение газа.
Теплоемкость равна
 (
),
постоянна.
(
),
постоянна.
18.Обратимые и необратимые процессы.Неравноценность теплоты и работы.Второе начало термодинамики.
Обратимый-Термодинам
процесс наз обратимым,если он может
происх как в прямом(если за цикл сов пол
 -протек
по час стрелке),так и в обратном(если
сов отр
-протек
по час стрелке),так и в обратном(если
сов отр
 -цикл
протек против час стрелки) направл,причем
если такой процесс происх сначала в
прямом,а затем в обратном напр и система
возр в исх состояние,то в окр среде и в
этой системе не происх никаких изменений.
Всякий процесс,не удовл этим условиям,явл
необратимым. Обратимый процесс-это
идеализация реальных процессов.их расм
важно по 2-м причинам:1.многие процессы
в природе и технике практически обратимы
2.обрат процессы явл наиболее эконом;имеют
макс терм кпд реальных тепловых
двигателей.
-цикл
протек против час стрелки) направл,причем
если такой процесс происх сначала в
прямом,а затем в обратном напр и система
возр в исх состояние,то в окр среде и в
этой системе не происх никаких изменений.
Всякий процесс,не удовл этим условиям,явл
необратимым. Обратимый процесс-это
идеализация реальных процессов.их расм
важно по 2-м причинам:1.многие процессы
в природе и технике практически обратимы
2.обрат процессы явл наиболее эконом;имеют
макс терм кпд реальных тепловых
двигателей.
Неравноценность теплоты и работы.Многолетняя чел практика привела к устан опр закономерн превр теплоты в работу и работы в теплоту(как общих для «обычных» и «необычных» систем,так и специф для тех и других).В резул анализа и было сформул 2начало терм.Из опр понятий теплоты и работы следует,что 2 рассматр в термодинамике формы передачи энергии не являются равноценными:в то время как работа может непосредственно пойти на↑любого вида энергии,теплота Q непосредственно,без предвар превращ в работу,привод лишь к↑ внутренней энергии системы.Эта неравноц Q и А не имела бы значения, если бы можно было без каких-либо трудностей превр теплоту в работу.Однако,в то время как при превр А в теплоту явл может огранизмен термодин состояния одного лить теплополуч тела(например, при нагрев посредством трения или при электронагреве),при преобраз Q в А наряду с охлаж теплоотд тела происх измен термодин состояния др тел, участв в этом процессе:или раб тела при незамк процессе,или др тел в замкн круговом процессе,когда этим телам раб тело непрем отдает часть получ им от нагревателя теплоты. В качестве таких «других тел» в тепловых машинах обычно служат хол-ки.
Второе начало
термодинамики: (исп понятие энтропии
и неравенство Клаузиуса)как закон возр
энтропии замкн системы при необр
процессах:любой необр процесс в замкн
системе происх так,что S
системы при этом возр.Краткая формулировка:в
процессах,происх в замкн системе,S
не убывает-речь идет о замкн системах,тк
в незамк иS можнет вести
себя любым образом-↑,↓,конст.
Энтропия-функция состояния,диф
которого явл
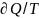 .
Для обр процессов:
.
Для обр процессов: S=0,
необрат цикл:
S=0,
необрат цикл: это только для замкн системы,если же
система обменивается теплотой с внеш
средой,то ее S может вести
себя любым образом. Соотн формул можно
предст в виде неравенства Кл-са:
это только для замкн системы,если же
система обменивается теплотой с внеш
средой,то ее S может вести
себя любым образом. Соотн формул можно
предст в виде неравенства Кл-са: ,т.е.
S замкн системы может либо
возр(НЕОБР
ПРОЦЕСС),ЛИБО КОНСТ(ОБРАТ ПРОЦЕСС).
Согласно Больцману:
,т.е.
S замкн системы может либо
возр(НЕОБР
ПРОЦЕСС),ЛИБО КОНСТ(ОБРАТ ПРОЦЕСС).
Согласно Больцману: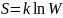 (W-термодинамическая
вероятность-число способов,кот может
быть реализовано данное состояние
макроскопической системы,k-пост
Больцмана).по формуле Больцмана:
толкование описывает закономерности
хаотического движения большого числа
частиц,сост замкн систему. Формулировки:1.
По Кельвину:невозможен круговой
процесс,един резул кот явл превращ
теплоты,пол от нагрев-ля,в эквивал ей
работу. 2. По Кла-усу: невозм круг
процесс,единс рез кот явл передача
теплоты от менее нагретого тела к более
нагр.
(W-термодинамическая
вероятность-число способов,кот может
быть реализовано данное состояние
макроскопической системы,k-пост
Больцмана).по формуле Больцмана:
толкование описывает закономерности
хаотического движения большого числа
частиц,сост замкн систему. Формулировки:1.
По Кельвину:невозможен круговой
процесс,един резул кот явл превращ
теплоты,пол от нагрев-ля,в эквивал ей
работу. 2. По Кла-усу: невозм круг
процесс,единс рез кот явл передача
теплоты от менее нагретого тела к более
нагр.
