6.Расчеты на прочность и жесткость при кручении. Статически неопределимые задачи. Расчеты на прочность и жесткость при кручении

Принципы расчетов на прочность, изложенные в главе 4 применительно к одноосному растяжению и сжатию, полностью справедливы и для случая кручения бруса. При кручении расчеты на прочность также делятся на проектировочные и поверочные. В основе расчетов лежит условие прочности

(7.34)

где τ_max - максимальное касательное напряжение в брусе, определяемое по вышеприведенным уравнениям в зависимости от формы сечения; [τ] - допускаемое касательное напряжение, равное части предельного напряжения для материала детали - предела прочности τ_в или предела текучести τ_т. Коэффициент запаса прочности устанавливается из тех же соображений, что и при растяжении. Например, для вала полого круглого поперечного сечения, с внешним диаметром D и внутренним диаметром d, имеем

,

(7.35)

где α=d/D - коэффициент полости сечения.

Условие жесткости такого вала при кручении имеет следующий вид:

,

(7.36)

где [φ_o] - допускаемый относительный угол закручивания

 

Статически неопределимые задачи при кручении При кручении, как и при растяжении, могут встретиться статически неопределимые задачи, для решения которых к уравнениям равновесия статики должны быть добавлены уравнения совместности перемещений. Нетрудно показать, что метод решения указанных задач при кручении и при растяжении один и тот же. Рассмотрим для примера брус, заделанный обоими концами в абсолютно жесткие стены (рис. 7.21). Отбросим заделки, заменив их действие неизвестными моментом M1 и M2. Уравнение совместности деформаций получим из условия равенства нулю угла закручивания в правой заделке: , где Ip1=πd14/32, Ip2=πd24/32. Крутящие моменты в сечениях бруса связаны следующим уравнением: . Решая совместно указанные уравнения относительно неизвестных моментов, получим: . Угол закручивания сечения C определяется из уравнения . Эпюры крутящих моментов и углов закручивания представлены на рис. 7.21.

7. Статические моменты сечения. Моменты инерции сечения. Преобразование моментов инерции при параллельном переносе осей.

Статические моменты сечения

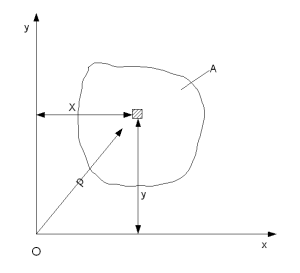
Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):

           

 

;                                                  (3)

                                       (4)

                                                         (5)

где y_c – расстояние от центра тяжести всего плоского сечения до оси x; x_c – расстояние от центра тяжести всего сечения до оси y.

Статический момент  сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:

                         (6)

В формулах (6) введены обозначения: А₁, А₂, …, А_n – площади простых элементов, составляющих плоское сложное сечение; x₁, y₁, x₂, y₂, x₃, y₃, … , x_n, y_n – координаты центров тяжести простых составляющих сложного плоского сечения относительно выбранных осей х и у.

Из выражений (4) можно определить координаты центра тяжести плоского сечения:

                                                             (7)

Для сложного поперечного сечения формулы (7) можно представить в следующем виде

                                (8)

Зависимости между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей х и х₁, а также у и у₁ имеют вид:

                                          (9)

где параметры a, b показаны на рис. 4.2.

                  Рис.4.2

Осевым моментом инерции сечения (second moment of area или second moment of inertia) относительно оси x называется сумма произведений элементарных площадок dA на квадрат их расстояний до данной оси, численно равная интегралу 

Jx= Ay2dA 

И относительно оси y:

Jy= Ax2dA 

где у — расстояние от элементарной площадки dA до оси х (смотри рисунок),  х — расстояние от элементарной площадки dA до оси у.

Полярным моментом инерции сечения относительно данной точки  (называемого полюсом ) называется сумма произведений элементарных площадок dA на квадрат их расстояний до этой точки:

J = A 2dA 

где    – расстояние от площадки dA до полюса, относительно которой вычисляется полярный момент инерции.

Центробежным моментом инерции сечения относительно осей x и y называется сумма произведений элементарных площадок dA на их расстояния до этих осей:

Jxy= AxydA 

где x,у — расстояние от элементарной площадки dA до осей х и y (смотри рисунок).

Центробежный момент инерции может быть положительным, отрицательным и, в частном случае, равным нулю. Если взаимно перпендикулярные оси x и y или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю. Jxy=0.

Полярный момент инерции относительно какой – либо точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку. J =Jx+Jy

Преобразование моментов инерции при параллельном переносе осей.

Ни хера нормального нет,почитайт лучше в книге про это ^