31. Ценообразование на рынке ценных бумаг.
Исторически первой моделью ценообразования капитальных активов является классическая концепция капитализации ожидаемых доходов. В соответствии с ней цена земли, как актива с бесконечным сроком службы определяется путем деления земельной ренты на ссудную ставку процента; цена объекта вложений с ограниченным сроком службы равна сумме всех ожидаемых за этот срок чистых доходов, приведенных к текущему моменту посредством коэффициента дисконтирования.
Основной недостаток классической концепции ценообразования на капитальные активы состоит в том, что она не учитывает вероятностный характер ожидаемых доходов и взаимозависимость доходностей всех финансовых инструментов. С позиций современной экономической теории отличие между дисконтированной суммой ожидаемых доходов капитального актива и его ценой примерно такое же, как между ценой блага, определенной по модели частичного равновесия (на отдельном рынке данного блага), и его ценой, установленной с помощью модели общего экономического равновесия. Тем не менее метод капитализации ожидаемых доходов в качестве модели ценообразования на рынке ценных бумаг может быть применим для финансовых инструментов с гарантированными номинальными доходами, т.е. для облигаций.
Цена облигации. При определении цены облигации решающими являются следующие ее характеристики: величина выплат владельцу облигации за период - купонный доход (z); предстоящий срок ее обращения (T); сумма гашения в конце срока обращения (B); рыночная ставка процента ;(i). Согласно концепции капитализации доходов
где
B0 - цена облигации в текущем (нулевом)
периоде. Обычно за все годы обращения
облигации дивиденды выплачиваются в
одинаковом размере: z1 = z2 = ... = zT = a; тогда
формула (5.11) принимает вид
Когда
рыночный курс облигации меньше значения,
получаемого по формуле (5.12), тогда следует
ожидать повышения курса, в противном
случае - понижения. Кроме нынешней цены
облигации может представлять интерес
ее цена на момент гашения (BT,/i>):
Она
показывает, какую сумму денег получит
владелец облигации в момент ее гашения
в случае реинвестирования всех дивидендов
под сложные проценты. Из четырех
параметров (a, B, i, T), определяющих цену
купонной облигации, два первых являются
известными константами. Рассмотрим,
как влияют на цену облигации изменения
срока ее обращения и рыночной ставки
процента. При a/B = i цена облигации равна
ее номиналу независимо от оставшегося
срока ее обращения, так как в этом случае
выражение (5.12) принимает следующий
вид:
Если a/B > i, то Bt > B, но по мере
приближения к моменту гашения облигации
разность (Bt - B) уменьшается. Когда a/B <
i, тогда Bt < B и Bt приближается к B снизу.
Проанализируем теперь, как влияет на ценность облигации колебание ставки процента. Из выражения (5.11) следует, что при ее изменении с i0 до i1 нынешняя ценность облигации изменится на: где zt при (t = T) - купонная выплата плюс сумма гашения облигации.
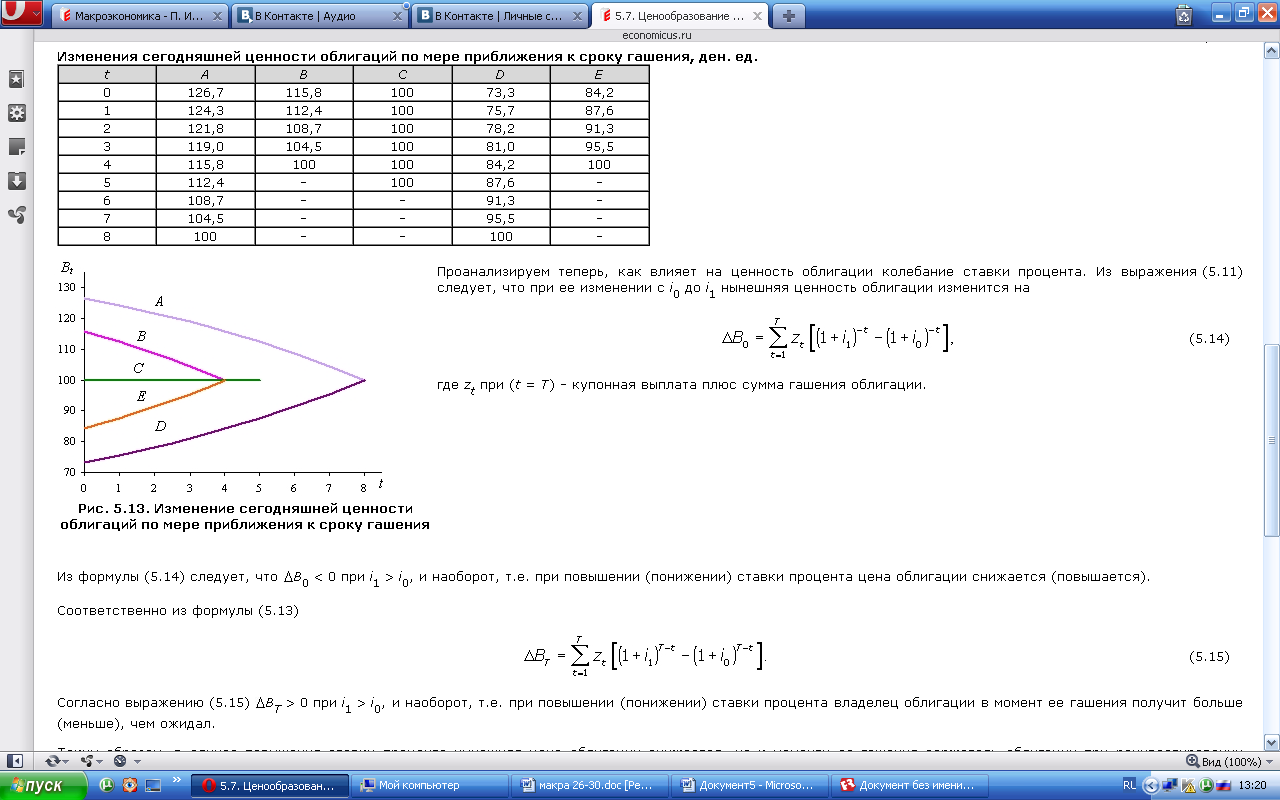Из
формулы (5.14) следует, что B0 < 0 при i1 >
i0, и наоборот, т.е. при повышении (понижении)
ставки процента цена облигации снижается
(повышается). Таким образом, в случае
повышения ставки процента нынешняя
цена облигации снижается, но к моменту
ее гашения держатель облигации при
реинвестировании дивидендов будет
иметь больше, чем ожидал. При понижении
ставки процента обладатель облигации
в текущем периоде окажется богаче, но
к моменту ее гашения он накопит меньшую
сумму, чем при исходной ставке процента.
Как изменяется цена облигации в каждом из периодов срока ее обращения при различных ставках процента, определяется по формуле
Обратим
внимание на то, что при снижении ставки
процента не удается предотвратить
снижения накоплений, ожидавшихся к
моменту гашения облигации, за счет ее
продажи по возросшей цене и предоставления
вырученной суммы в ссуду под сложные
проценты (135,6·1,045 = 165). Пересечение кривых,
представляющих динамику текущей цены
облигации в течение срока ее обращения
при различных ставках процента (см. рис.
5.14), свидетельствует о том, что существует
определенный момент, в который текущая
цена облигации не зависит от изменения
ставки процента. В приведенном примере
таким моментом является четвертый год.
Эту особенность динамики ценности
облигации (капитализируемого дохода)
в теории финансов используют при
выработке рекомендаций по нейтрализации
риска от изменения рыночной ставки
процента.
Цена акции
В отличие от облигации факторы, определяющие ценность акции, являются вероятностными величинами. Будет ли на простую акцию периодически выплачиваться дивиденд, а если будет, то в каком размере, - эти вопросы руководство фирмы решает в оперативном порядке в зависимости от результатов деятельности фирмы и стратегии ее развития. Эмитент акции не берет на себя обязательство ее выкупа через какое бы то ни было время, поэтому акция не имеет цены гашения. Вместо нее инвестор имеет дело с прогнозируемым на определенный момент рыночным курсом акции, который в силу отмеченных обстоятельств очень изменчив. В настоящее время существует несколько концепций определения цены рискового актива. Традиционный способ основан на использовании формулы (5.11) в которой zt представляет ожидаемый доход на акцию в период t. Теория портфеля послужила основой возникновения двух современных концепций ценообразования на рынке рисковых активов - модели рынка10 и модели ценообразования капитальных активов CAPM (capital asset pricing model).