12.4. Основы теории m-фильтров. Каскадное включение фильтров

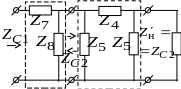
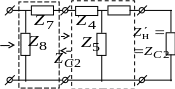
Для увеличения крутизны характеристики  = f(w) в начале полосы затухания, для получения заданного значения затухания при определенной частоте и для меньшей зависимости Z_С от частоты в полосе прозрачности применяют полузвенья m-фильтров каскадно включаемые с k-фильтрами (рис. 12.6).

При каскадном соединении фильтров друг с другом всегда соблюдаются принципы согласованности (рис. 12.7)

(12.5)

Г-образное

полузвено

m-фильтра

Т-образный

фильтр

k-типа

Рис. 12.6. Варианты включения фильтров m-типа и k-типа

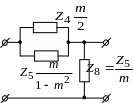
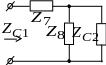
Рис. 12.7. Принципы согласования фильтров

при каскадном соединении

Решим уравнения относительно Z_С1 и Z_C2:

.

Для Г-образного фильтра При этом характеристические сопротивления будут равны

(12.6)

Входное сопротивление второго каскада

. (12.7)

Сопротивление Z₈ в Г-звене m-фильтра берут равным , где m = 0-1. Подставим Z₈ в уравнения (12.6) и (12.7) и, приравняв их друг другу, получим формулу для  Z₇:

.

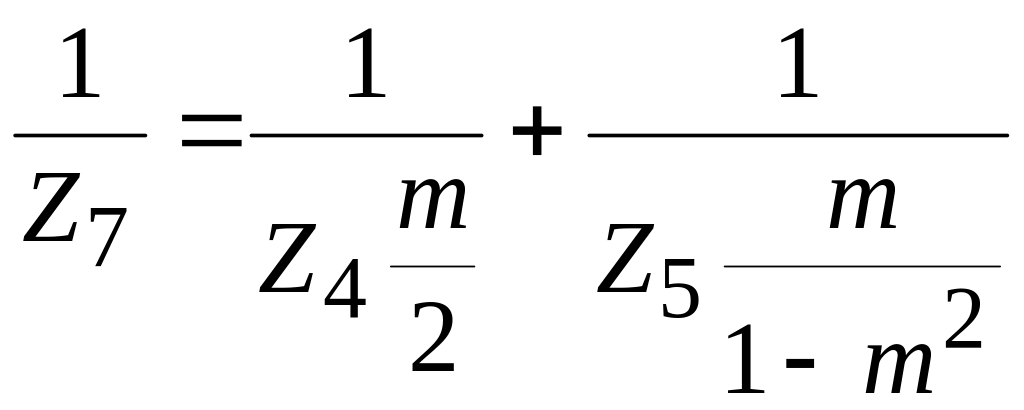Сопротивление Z₇ образовано двумя параллельно соединенными сопро­тивлениями и . Данный тип m-фильтра называется параллельно-производным.

Границы прозрачности у m-фильтра определяют так же, как у k-фильтра. Следует отметить, что границы полосы прозрачности для k-фильтра и каскадно включенного и согласованного с ним m-фильтра совпадают. Результирующее затухание всего фильтра  равно сумме затуханий отдельных фильтров (рис. 12.8).

На рис. 2.8 обозначена резонанская частота w_P, при которой противоположного характера сопротивления и вступают в резонанс. В области частот от _C до . резко возрастает, что очень существенно, так как получается большое затухание в начале полосы затухания, где мало. Уменьшение при компенсируется ростом . Коэффициент фазы всего фильтра .

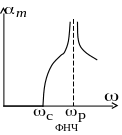
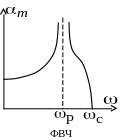
Рис. 12.8. Полосы прозрачности m-фильтров

При m » 0,5-0,6 сопротивление остается приблизительно постоянным почти во всей полосе прозрачности, резко уменьшаясь только вблизи частоты среза (рис. 12.9).

Аналогичный анализ для Г-образного полузвена m-фильтра показывает, что сопротивление Z₁₀ состоит из двух последовательных сопротивлений и (рис. 12.10). Здесь возможен режим резонанса напряжений при (сопротивления Z₁ и Z₃ имеют разные знаки).

Зависимости для и здесь те же. Наличие двух резонансных частот объясняется двумя условиями резонанса.

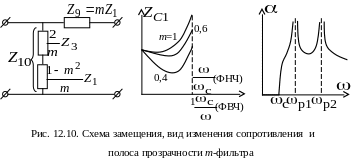
Приложение

Соответствие некоторых функций (оригиналов)

и их изображений по Лапласу

Оригинал	Изображение
A	A / p
sin(t + )
cos(t + )
t