5.2. Работа расширения

Работа в термодинамике, также как и в механике, определяется произведением действующей на рабочее тело силы на путь ее действия.

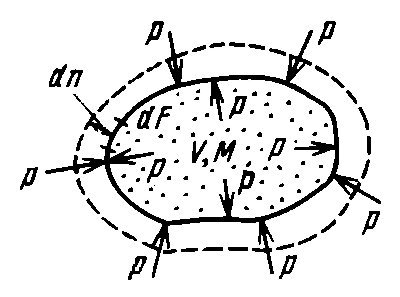
Рисунок 6 – К определению работы расширения.

Допустим, что имеется газ с параметрами М или m (масса) и V (объем), заключенный в эластичную оболочку с поверхностью F (рис. 3). Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него средой.

Газ действует на каждый элемент оболочки dF c силой, равной p·dF, и перемещая ее по нормали к поверхности на расстояние dn, совершает при этом элементарную работу p·dF·dn.

Общую работу, совершенную в течение бесконечно малого процесса, получим, интегрируя данное выражение по всей поверхности F оболочки:

Из рисунка 4 очевидно, что интеграл по поверхности соответствует изменению объема ∆V:

Следовательно

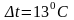
При конечном изменении объема работа против сил внешнего давления, называемая работой расширения, выражается зависимостью:

Работа δL и изменение объема ∆V всегда имеют одинаковые знаки, отсюда:

1. δL>0 и ∆V>0 – при расширении работа тела положительна, при этом само тело совершает работу;

2. δL<0 и ∆V<0 – при сжатии работа тела отрицательна, при этом не тело совершает работу, а на его сжатие затрачивается работа.

Если процесс расширения протекает не с 1 кг газа, а с m (кг), то уравнение работы расширения примет вид:

Для исследования равновесных процессов в термодинамике используют рυ-диаграммы, где работа изменения объема эквивалентна площади под кривой процесса (рис. 7).

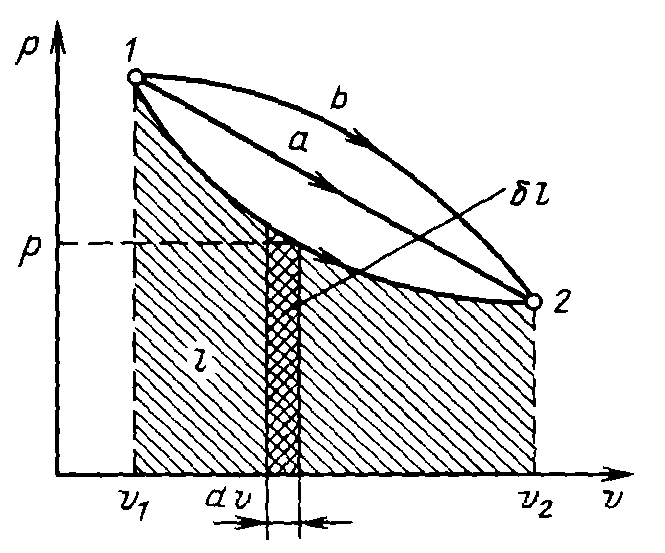
Рисунок 7 – Графическое изображение работы в рυ-координатах.

Каждому пути перехода соответствует своя работа расширения, следовательно, работа зависит от характера термодинамического процесса, а не является функцией только начального и конечного состояния системы.

5.3. Теплота

Помимо макрофизической формы передачи энергии – работы существует также и микрофизическая, т.е. осуществляемая на молекулярном уровне. В этом случае энергия может быть передана системе без совершения работы. Мерой количества энергии, переданной микрофизическим путем, является теплота.

Теплота может передаваться либо при непосредственном контакте между телами (теплопроводность, конвекция), либо на расстоянии (излечение) при обязательном наличии градиента температур.

5.4. Аналитическое выражение первого закона термодинамики

Пусть 1 кг рабочего тела совершает некоторый процесс (рис. 8), на элементарном участке которого a-b подводится бесконечно малое количество энергии в форме теплоты dq; при этом температура и объем тела увеличиваются соответственно на бесконечно малые величины dT и dυ.

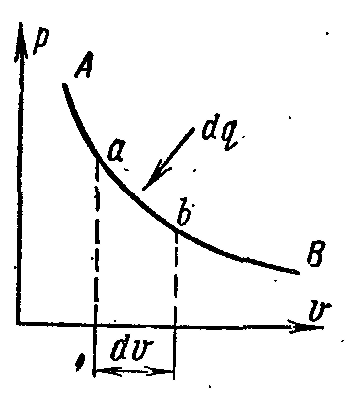
Рисунок 8.

С повышением температуры тела на dT увеличивается скорость молекул или увеличивается его внутренняя кинетическая энергия.

С увеличением объема тела на dυ увеличивается расстояние между молекулами, что связано с увеличением его внутренней потенциальной энергии.

Сумма изменений внутренней кинетической и внутренней потенциальной энергии представляет полное изменение внутренней энергии du.

С увеличением объема на dυ тело совершает внешнюю работу по преодолению внешних сил, которую обозначают δl.

Если, в рабочем теле не происходит каких-либо других явлений и отсутствует кинетическая энергия видимого движения, то, согласно закону сохранения энергии, для элементарного процесса характерна следующая зависимость:

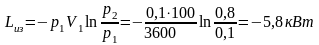
Полученное выражение является математическим выражением первого начала термодинамики. Оно формулируется следующим образом: подведенная к рабочему телу энергия в форме удельной теплоты расходуется на изменение удельной внутренней энергии и на совершение телом внешней работы.

Величины, входящие в уравнение первого закона термодинамики могут быть как положительными, так и отрицательными.

Несмотря на всю простоту первого закона термодинамики, имеется большое количество его формулировок.

1. Невозможно возникновение или уничтожение энергии. Эта формулировка говорит о невозможности возникновения энергии из ничего и уничтожении ее в ничто.

2. Любая форма движения способна и должна превращаться в любую другую форму движения. Эта формулировка, данная Энгельсом, подчеркивает неуничтожаемость энергии и ее способность взаимопревращаться в любые другие виды энергии.

3. Создание вечного двигателя первого рода невозможно. Понимается невозможность создания машины, производящей работу из ничего.

И многие другие.