
- •Тема 6: «Теплоемкость газов. Энтропия» 33
- •Тема 7: «Термодинамические процессы идеальных газов» 43
- •Тема 8: «Второй закон термодинамики» 57
- •Тема 9: «Характеристические функции и термодинамические потенциалы. Равновесие систем» 71
- •Тема 10: «Водяной пар» 83
- •Тема 11. Истечение газов и паров 89
- •Тема 1: Основные понятия и определения
- •1.1. Основные термодинамические параметры состояния
- •4. Внутренняя энергия.
- •5. Энтальпия,
- •6. Энтропия,
- •1.2. Термодинамическая система
- •1.3. Термодинамический процесс
- •1.4. Теплота и работа
- •1.5. Термодинамическое равновесие
- •Контрольные вопросы
- •Тема 2: «Состояние идеального газа»
- •2.1. Основные законы идеальных газов
- •2.2. Уравнение состояния идеального газа
- •Тема 4: «Реальные газы»
- •4.1. Уравнение состояния Ван-дер-Ваальса
- •4.2. Уравнения м.П. Вукаловича и и.И. Новикова
- •Контрольные вопросы
- •Тема 5: «Первый закон термодинамики»
- •5.1. Внутренняя энергия
- •5.2. Работа расширения
- •5.3. Теплота
- •5.4. Аналитическое выражение первого закона термодинамики
- •5.5. Энтальпия
- •Контрольные вопросы
- •Тема 6: «Теплоемкость газов. Энтропия»
- •6.1. Основные определения
- •6.2. Удельная (массовая), объемная и мольная теплоемкости газов
- •6.3. Теплоемкость в изохорном и изобарном процессе
- •6.4. Молекулярно-кинетическая и квантовая теории теплоемкости
- •6.5. Истинная и средняя теплоемкости
- •6.6. Зависимость теплоемкости от температуры
- •6.7. Отношение теплоемкостей ср и сυ. Показатель адиабаты
- •6.8. Определение qp и qυ для идеальных газов
- •6.9. Теплоемкость смеси идеальных газов
- •6.10. Энтропия
- •Контрольные вопросы
- •Тема 7: «Термодинамические процессы идеальных газов»
- •7.1. Основные определения
- •7.2. Изохорный процесс
- •7.3. Изобарный процесс
- •7.4. Изотермический процесс
- •7.5. Адиабатный процесс
- •7.6. Политропные процессы
- •Контрольные вопросы
- •Тема 8: «Второй закон термодинамики»
- •8.1. Основные положения
- •8.2. Круговые термодинамические процессы (циклы)
- •8.3. Термический кпд и холодильный коэффициент циклов
- •8.4. Прямой обратимый цикл Карно
- •8.5. Обратный обратимый цикл Карно
- •8.6. Математическое выражение второго закона термодинамики
- •8.7. Изменение энтропии в обратимых и необратимых процессах
- •Контрольные вопросы
- •Тема 9: «Характеристические функции и термодинамические потенциалы. Равновесие систем»
- •Характеристические функции
- •Физический смысл изохорно-изотермического и изобарно-изотермического потенциалов
- •Термодинамическое учение о равновесии
- •9.4. Общие условия равновесия термодинамической системы
- •Контрольные вопросы
- •Тема 10: «Водяной пар»
- •10.1. Основные понятия и определения
- •Контрольные вопросы
- •Тема 11. Истечение газов и паров
- •11.1. Первый закон термодинамики в применении к потоку движущегося газа
- •11.2. Работа проталкивания
- •11.3. Располагаемая работа
- •11.4. Адиабатный процесс истечения
- •11.5. Истечение из суживающегося сопла
- •11.6. Истечение идеального газа из комбинированного сопла Лаваля
- •Контрольные вопросы
7.3. Изобарный процесс
Изобарным называется процесс, протекающий при постоянном объеме. Кривая процесса называется изобара.

Рисунок 13 – р,υ- и T,s-диаграммы изобарного процесса.
Из уравнения состояния идеального газа

При р=const объем газа изменяется прямо пропорционально абсолютным температурам:

При расширении газа его температура возрастает, при сжатии – уменьшается.
Удельная работа изменения объема выражается уравнением:
или

Удельная располагаемая (полезная) внешняя работа

Изменение удельной внутренней энергии

Основное уравнение первого закона термодинамики при р=const принимает вид:

Следовательно, удельное количество теплоты, сообщенное телу в изобарном процессе, при постоянной теплоемкости

При переменной теплоемкости

Часть сообщенного удельного количества теплоты q1-2,р, равное р(υ2–υ1), переходит в работу расширения, а другая часть идет на увеличение удельной внутренней энергии тела.
Для обратимого изобарного процесса при постоянной теплоемкости изменение удельной энтропии находится по уравнению
Изобара на Т,s-диаграмме изображается кривой, обращенной выпуклостью вниз. Площадь под изобарой в некотором масштабе изображает некоторое количество теплоты qp, сообщенное газу и равное изменению удельной энтальпии i2–i1.
Все изобары при одной и той же температуре имеют одинаковые угловые коэффициенты. Горизонтальные расстояния между изобарами различных давлений при Т=const (рис. 12) определяются по уравнению

Из данного уравнения следует, что расстояние между изобарами зависит от давлений и природы газа. Чем больше давление газа, тем ближе изобара к оси ординат.
В случае осуществления изобарного и изохорного процессов в одном температурном интервале возрастание удельной энтропии будет больше в изобарном процессе, так как ср всегда больше сυ. Поэтому изобара является более пологой кривой по сравнению с изохорой (рис. 12).
7.4. Изотермический процесс
Изотермическим называется процесс, протекающий при постоянной температуре. Кривая процесса называется изотерма.
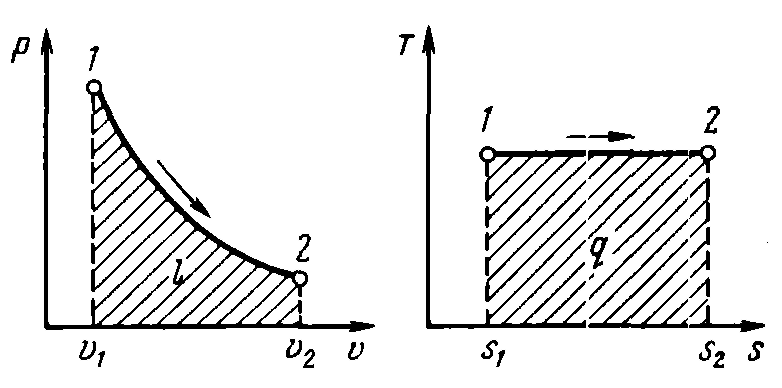
Рисунок 14 – р,υ- и T,s-диаграммы изотермического процесса.
Из уравнения состояния идеального газа

или

При постоянной температуре объем газа изменяется обратно пропорционально его давлению (закон Бойля-Мариотта).
На р,υ-диаграмме (рис. 14) изотермический процесс представляет собой равнобокую гиперболу.
Основное уравнение первого закона термодинамики при T=const принимает вид:

или

Количество подведенной к рабочему телу теплоты численно равно работе изменения объема.
Удельная работа изменения объема

Но из уравнения
изотермы
имеем
 ,
поэтому
,
поэтому

Интегрируя последнее выражение, получим

При переходе к десятичному логарифму

Удельная располагаемая внешняя работа l´ определяется по формуле

Таким
образом, в изотермическом процессе
идеального газа
 ,
или удельная работа изменения объема,
располагаемая (полезная) работа и
удельное количество теплоты, полученное
телом, равны между собой.
,
или удельная работа изменения объема,
располагаемая (полезная) работа и
удельное количество теплоты, полученное
телом, равны между собой.
Теплоемкость в изотермическом процессе

Энтальпия
и внутренняя энергия идеального газа
не меняются, т.е.
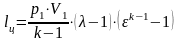 и
и
 .
.
Для определения изменения удельной энтропии используют уравнение

Откуда

Удельное количество теплоты, участвующее в изотермическом процессе, равно произведению изменения удельной энтропии ( ) на абсолютную температуру Т.
