2. равновесное состояние

РАВНОВЕСНОЕ СОСТОЯНИЕ - состояние, в которое приходит термодинамич. система при постоянных внеш. Условиях. характеризуется постоянством во времени термодинамич. параметров и отсутствием в системе потоков вещества и энергии.

3. макроскопические параметры

Макроскопические параметры- параметры больших масштабов (масса газа, давление, обьем, температура)

4. модель идеального газа

Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. В этой модели газ рассматривается в виде совокупности молекул — шариков очень малых размеров и почти не взаимодействующих между собой, т.е. при рассмотрении законов идеального газа пренебрегают собственным объемом молекул (по сравнению с объемом сосуда, в котором он находится) и силами их взаимного притяжения; при соударениях молекул друг с другом и со стенками сосуда действуют силы упругого отталкивания. Идеального газа в природе не существует — это упрощенная модель реального газа.

Реальный газ становится близким по свойствам к идеальному, когда он достаточно нагрет и разрежен. Некоторые газы, например, воздух, кислород, азот, даже при обычных условиях (комнатная температуре и атмосферное давление) мало отличаются от идеального газа. Особенно близки по своим свойствам к идеальному газу гелий и водород.

Существует два основных подхода к изучению газов: с учетом их молекулярного строения и использования микропараметров (масса и скорость молекул, их концентрация и т. д.) и без учета молекулярного строения, когда газы описываются макропараметрами (давлением р, объемом V, температурой T, полной массой всех молекул газа М).

В рамках молекулярно-кинетической теории давление, производимое газом на стенки сосуда, возникает вследствие того, что молекулы газа, беспорядочно двигаясь, ударяются о стенки сосуда, передавая им при каждом соударении свой импульс. Суммарный импульс, переданный за единицу времени единице площади, — это и есть давление, производимое газом.

5. Максвелл

Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяеться. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v1 и v2 . На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число молекул в единице объема; компоненты скоростей которых лежат в интервале от до , от до и от до , определяются функцией распределения Максвелла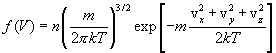

где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, чтсг число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет вид

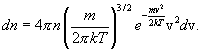
Распределение Максвелла достигает максимума при скорости , т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.

Кривая распределения Максвелла позволит найти среднюю арифметическую скорость

Таким образо:

С Повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.

6 Уравнение состояние идеального газа

Соотношение p = nkT, связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

Здесь N – число молекул в сосуде, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть: R = 8,31 Дж/моль·К.

Соотношение называется уравнением состояния идеального газа.

Для одного моля любого газа это соотношение принимает вид: pV=RT

Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный V0 = 0,0224 м3/моль = 22,4 дм3/моль