Метод прогонки

Для решения систем A x = b с трехдиагональной матрицей наиболее часто применяется метод прогонки, являющийся адаптацией метода Гаусса к этому случаю.

Запишем систему уравнений

d₁x₁ + e₁x₂                                            = b₁            c₂x₁ + d₂x₂ + e₂x₃                                 = b₂                       c₃x₂ + d₃x₃ + e₃x₄                      = b₃                                     ...       ...       ...                                  c_n-1x_n-2 + d_n-1x_n-1 + e_n-1x_n = b_n-1                                                     c_nx_n-1 + d_nx_n = b_n

в матричном виде: A x = b где

A=

Выпишем формулы метода прогонки в порядке их применения.

1. Прямой ход метода прогонки (вычисление вспомогательных величин):

   2 = -e1 / d1 2 = b1 / d1 i+1 = -ei / [di + cii], i=2, ..., n-1  i+1 = [-cii + bi] / [di + cii], i=2, ..., n-1

   (1.9)

2. Обратный ход метода прогонки (нахождение решения):

xn = [-cn n + bn] / [dn + cnn] xi = i+1 xi+1 + i+1, i = n-1, ..., 1

Билет№31

Метод простых итерации

Суть метода простых итераций состоит в переходе от уравнения

f(x)= 0  (*)

  к эквивалентному уравнению

x =φ(x). (**)

Этот переход можно осуществить разными способами, в зависимости от вида f(x). Например, можно положить

φ(x) =x+bf(x),(***)

где   b = const, при этом корни исходного уравнения не изменятся.

Если известно начальное приближение к корню x₀, то новое приближение

x₁=φx(₀),

т.е. общая схема итерационного процесса:

x_k+1=φ(x_k).(****)

Наиболее простой критерий окончания процесса

|x_k+1-x_k|<ε.

Критерий сходимости метода простых итераций:

 если вблизи корня |φ^/(x)| < 1, то итерации сходятся. Если указанное условие справедливо для любого x, то итерации сходятся при любом начальном приближении.

Исследуем выбор константы b с точки зрения обеспечения максимальной скорости сходимости. В соответствии с критерием сходимости наибольшая скорость сходимости обеспечивается при |φ^/(x)| = 0. При этом, исходя из (***), b = –1/f ^/(x), и итерационная формула (****) переходит в х_i=х_i-1-f(x_i-1)/f/ (x_i-1).-т.е. в формулу метода Ньютона. Таким образом, метод Ньютона является частным случаем метода простых итераций, обеспечивающим самую высокую скорость сходимости из всех возможных вариантов выбора функции φ(x).

Билет№32

Метод Ньютона

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть   — определённая на отрезке   и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где α — угол наклона касательной в точке  .

Следовательно искомое выражение для   имеет вид:

Билет№33

Метод золотого сечения Метод золотого сечения позволяет исключать интервалы, вычисляя только одно значение функции на каждой итерации. В результате двух рассмотренных значений функции определяется интервал, который должен использоваться в дальнейшем. Этот интервал будет содержать одну из предыдущих точек и следующую точку, помещаемую симметрично ей. Точка делит интервал на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т. е. равно так называемому «золотому сечению».

Деление интервала на неравные части позволяет найти еще более эффективный метод. Вычислим функцию на концах отрезка [a, b] и положим a=x₁, b=x₂. Вычислим также функцию в двух внутренних точках x₃, x₄. Сравним все четыре значения функции и выберем среди них наименьшее. Пусть, например, наименьшим оказалось f(x₃). Очевидно, минимум находиться в одном из прилегающих к нему отрезков. Поэтому отрезок [x₄,b] можно отбросить и оставить отрезок [a,x₄].

 

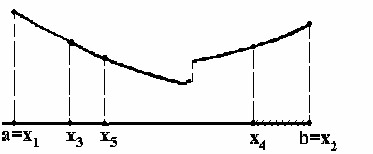
Первый шаг сделан. На отрезке [a,x₄] снова надо выбрать две внутренние точки, вычислив в них и на концах значения функции и сделать следующий шаг. Но на предыдущем шаге вычислений мы уже нашли функцию на концах нового отрезка [a,x₄] и в одной его внутренней точке x₄. Потому достаточно выбрать внутри [a,x₄] еще одну точку x₅ определить в ней значение функции и провести необходимые сравнения. Это вчетверо уменьшает объем вычислений на одном шаге процесса. Как выгодно размещать точки? Каждый раз оставшийся отрезок делиться на три части и затем отбрасывается один из крайних отрезков. Обозначим первоначальный интервал неопределенности через D.

 

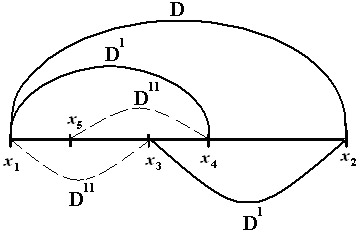
Так как в общем случае может быть отброшен любой из отрезков Х₁,Х₃ или Х₄,Х₂ то выберем точки Х₃ и Х₄ так, чтобы длины этих отрезков были одинаковы: 

x₃-x₁=x₄-x₂.

После отбрасывания получится новый интервал неопределенности длины D′. Обозначим отношение D/D′ буквой φ:

φ = D/D′.

Далее продолжим процесс аналогично. Для этого интервал D′ разделим подобно интервалу D ,

 то есть положим   , где   - следующий интервал неопределенности. Но 

 по длине равен отрезку, отброшенному на предыдущем этапе, то есть 

Поэтому получим: . Это приводит к уравнению   или, что то же  .  Положительный корень этого уравнения дает

.

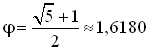Билет№34

интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение.

Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для   пар чисел  , где все   различны, существует единственный многочлен   степени не более  , для которого  .

В простейшем случае ( ) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

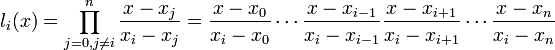
 обладают следующими свойствами:

• являются многочленами степени 

• 

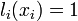
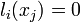•  при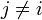 

Отсюда следует, что  , как линейная комбинация  , может иметь степень не больше  , и 

 Формула Лагранжа

Интерполяционная формула Лагранжа обеспечивает построение алгебраического многочлена P_n(x) для произвольно заданных узлов интерполирования. Для n + 1 различных значений аргумента x₀, x₁, ..., x_n и соответствующих значений функции f(x₀) = y₀, f(x₁) = y₁, ...,f(x_n) = y_n интерполяционная формула Лагранжа имеет вид

,

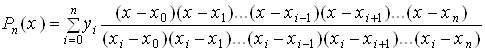где х -  значение аргумента функции, расположенного в интервале [x₀, x_n].

Билет№35

 методика аппроксимации эмпирических данных Эмпирические данные, как правило, задаются числовыми рядами значений двух величин: независимой (х_k) и зависимой (у_k) , каждая из которых кроме определенной регулярной составляющей может содержать и случайные составляющие самой различной природы, обусловленные как статистической природой изучаемых процессов, так и внешними факторами процессов измерений и преобразования данных (шумы, помехи, ошибки измерений). Независимая переменная x_k обычно полагается детерминированной, а ее случайная составляющая "переносится" на зависимую переменную y_k. Полагается также, что значения случайной составляющей зависимой переменной распределены по некоторому вероятностному закону (например – нормальному). При выполнении аппроксимации данных предполагается существование определенной детерминированной связи y(x) между регулярными составляющими этих двух числовых рядов на статистически значимом уровне, достаточном для ее выявления на уровне случайных составляющих. Задача выявления такой закономерности относится к числу неопределенных и неоднозначных, результат которой зависит от трех основных субъективных факторов:

• выбора меры близости зависимой переменной к искомой функции и метода построения приближения (параметров математической модели);

• выбора подходящего класса функции аппроксимации (степенной, тригонометрической и пр.), отвечающего физической природе моделируемого процесса;

• метода оптимизации порядка модельной функции или числа членов ряда аппроксимирующего выражения.

Отсюда следует, что оптимальная аппроксимация может быть обеспечена только достаточно гибкими интерактивными алгоритмами на основе многоэтапных итерационных процессов с возможностью коррекции на каждом этапе.

Метод наименьших квадратов (МНК) - метод оценки параметров модели на основании экспериментальных данных, содержащих случайные ошибки. В основе метода лежат следующие рассуждения: при замене точного (неизвестного) параметра модели приблизительным значением необходимо минимизировать разницу между экспериментальными данными и теоретическими (вычисленными при помощи предложенной модели). Это позволяет рассчитать параметры модели с помощью МНК с минимальной погрешностью.

Мерой разницы в методе наименьших квадратов служит сумма квадратов отклонений действительных (экспериментальных) значений от теоретических. Выбираются такие значения параметров модели, при которых сумма квадратов разностей будет наименьшей – отсюда название метода:

 = min

где Y – теоретическое значение измеряемой величины, y – экспериментальное.

Билет№36