Хроматические аберрации

Хроматические аберрации. Излучение обычных источников света обладает сложным спектральным составом, что приводит к возникновению хроматических аберраций. В отличие от геометрических, хроматические аберрации возникают и в параксиальной области.Дисперсия света порождает два вида хроматических аберраций: хроматизм положения фокусов и хроматизм увеличения. Первая характеризуется смещением плоскости изображения для разных длин волн, вторая - изменением поперечного увеличения. Подробнее см.Хроматическая аберрация.

Аберра́ция оптической системы — ошибка или погрешность изображения в оптической системе, вызываемая отклонением луча от того направления, по которому он должен был бы идти в идеальной оптической системе. Аберрацию характеризуют различного вида нарушения гомоцентричности^[1] в структуре пучков лучей, выходящих из оптической системы.

Величина аберрации может быть получена как сравнением координат лучей путём непосредственного расчёта по точным геометро-оптическим формулам, так и приближённо — с помощью формул теории аберраций.

При этом возможно характеризовать аберрацию как критериями лучевой оптики, так и на основе представлений волновой оптики. В первом случае отступление от гомоцентричности выражается через представление о геометрических аберрациях и фигурах рассеяния лучей в изображениях точек. Во втором случае оценивается деформация прошедшей через оптическую систему сферической световой волны, вводя представление о волновых аберрациях. Оба способа описания взаимосвязаны, описывают одно и то же состояние и различаются лишь формой описания.

Как правило, если объектив обладает большими аберрациями, то их проще характеризовать величинами геометрических аберраций, а если малыми, то на основе представлений волновой оптики.

Аберрации можно разделить на монохроматические, то есть присущие монохромным пучкам лучей, и хроматические.

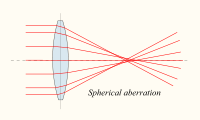
Сферическая аберрация

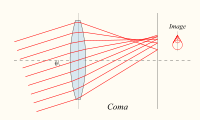
Кома

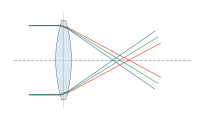
Хроматическая аберрация

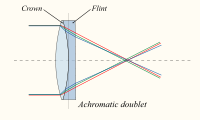
Ахроматическая линза

Монохроматические аберрации

Такие погрешности изображений присущи всякой реальной оптической системе, и принципиально неустранимы. Их возникновение объясняется тем, что преломляющие поверхности неспособны собрать в точку сколько-нибудь широкие пучки лучей, падающие на них под большими углами.

Эти аберрации приводят к тому, что изображением точки является некоторая размытая фигура (фигура рассеяния), а не точка, что, в свою очередь, отрицательно влияет на чёткость изображения и нарушает подобие изображения и предмета.

Теория аберраций

Теория геометрических аберраций устанавливает функциональную зависимость аберраций от координат падающего луча и конструктивных элементов оптической системы — от радиусов её поверхностей, толщин, показателей преломления линз и т. д.

Монохроматические аберрации третьего порядка

Теория аберраций ограничивается приближённым представлением составляющих аберраций (δg ' и δG' ) в виде ряда, члены которого содержат некие коэффициенты (суммы переменных) а₁, а₂,…а_k, зависящие только от конструктивных элементов оптической системы и от положения плоскостей объекта и входного зрачка, но не зависящие от координат луча. Так например, меридиональная^[2] составляющая аберрации третьего порядка может быть представлена формулой:

где   и   — координаты луча, входящие в качестве сомножителей членов ряда.

Число таких коэффициентов аберраций третьего порядка равно пяти и, как правило, они обозначаются буквами S_I, S_II, S_III, S_IV, S_V.

Причём, в целях упрощения анализа, предполагают, что в формулах только один из коэффициентов не равен нулю, и определяет соответствующую аберрацию.

Каждым из пяти коэффициентов определяется одна из так называемых пяти аберраций Зейделя:

1. S_I — сферическая аберрация;

2. S_II — кома;

3. S_III — астигматизм;

4. S_IV — кривизна поля (поверхности) изображения;

5. S_V — дисторсия.

В реальных системах отдельные виды монохроматических аберраций почти никогда не встречаются. В действительности, наблюдается сочетание всех аберраций, а исследование сложной аберрационной фигуры рассеяния методом выделения отдельных видов аберраций (любого порядка) — не более чем искусственный приём, облегчающий анализ явления.