12. Свойства средней арифметической. Способы ее исчисления.

Средняя арифметическая обладает рядом математических свойств:

1. Если xi – постоянная величина (xi=C), то ее средняя 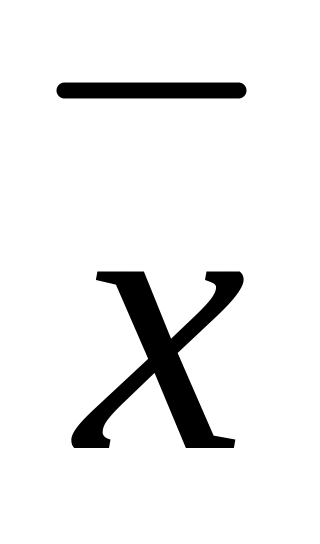= C

2. Сумма отклонений значений признака от его средней арифметической равна нулю:

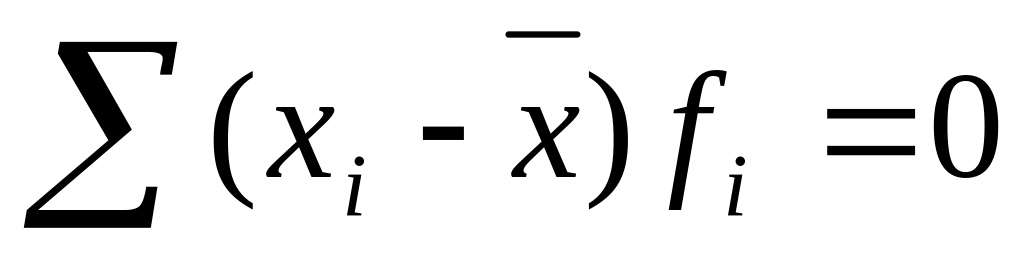
3. Если все значения признака уменьшить/увеличить на постоянную величину С, то уменьшится/увеличится на С:

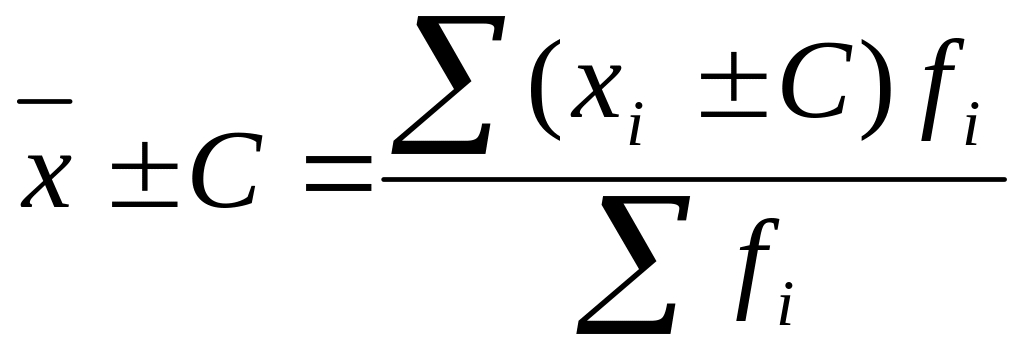
4. От уменьшения или увеличения частот (fi) каждого значения признака в m раз величина не изменится:

5. Если все значения признака уменьшить (увеличить) в d раз, то также уменьшится или увеличится в d раз.

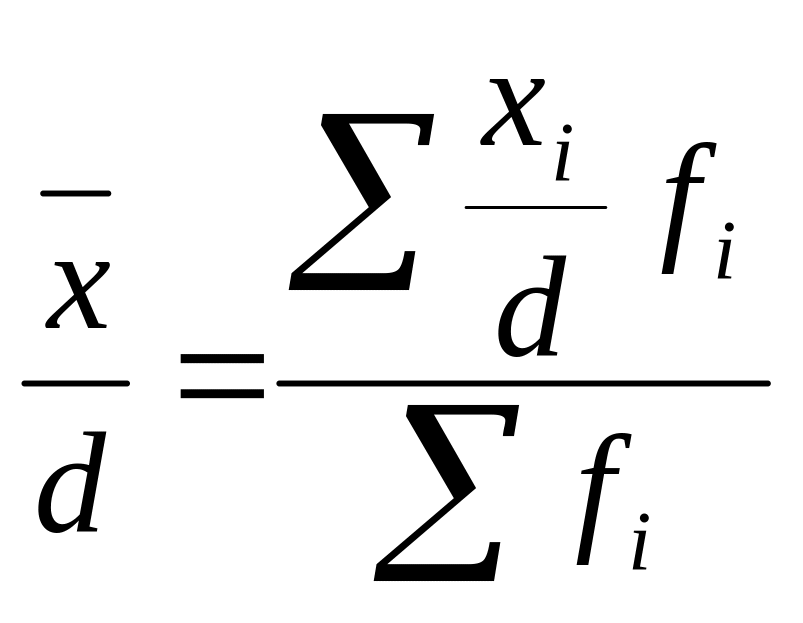
6. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина. Если исходные данные не сгруппированы, то используют простую среднюю арифметическую:

Если исходные данные сгруппированы, то используется взвешенная средняя арифметическая:

Если данные сгруппированы и все частоты равны между собой, то можно использовать среднюю арифметическую простую.

Если результаты наблюдения представлены в виде интервального ряда распределения, то для расчета средней в качестве xi берутся середины интервалов.

Свойства средней арифметической используются для ее расчета способом моментов. (методом отсчета от условного нуля). Он используется в случае вариационных рядов с равными интервалами.

; - момент первого порядка (условная средняя)

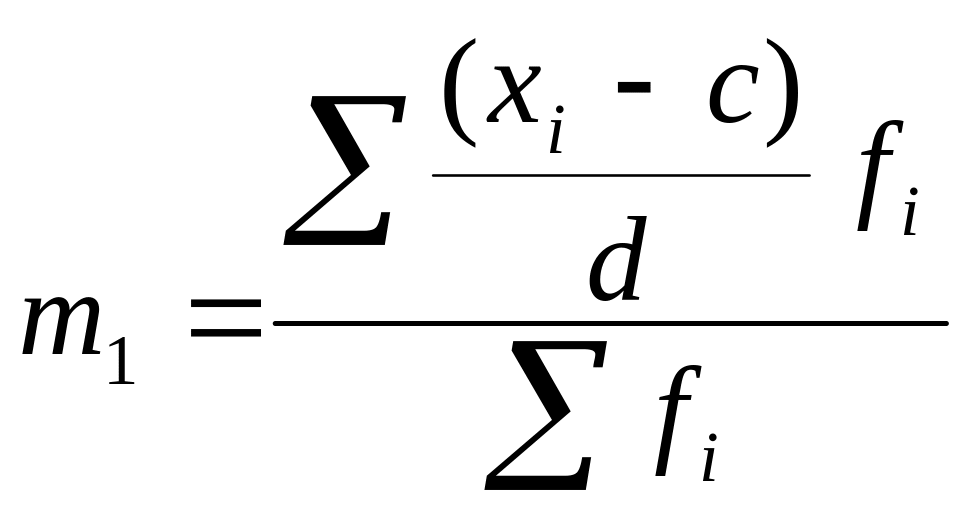, где за d берут длину интервала, а за c – середину интервала, находящегося в центре ряда или середину интервала с наибольшей частотой.

12. Структурные средние, методика их исчисления в дискретных и интервальных рядах распределения.

Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен.

В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место (каждое четвертое, пятое, десятое, двадцать пятое и т.д.) в ранжированном вариационном ряду. Такие показатели носят общее название квантилей или градиентов. Некоторые из них имеются особые наименования: квартили, квинтили, децили и перцентили. В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили, децили и перцентили. Квартили - значения признака, делящие ранжированную совокупность на четыре равновеликие части. Децили - варианты, делящие ранжированный ряд на десять равных частей. Перцентили - значения признака, делящие ряд на сто частей. Квартилей насчитывается три, а децилей – девять, а перцентилей – девяносто девять.

Мода – наиболее часто встречающееся значение признака (Мо), для дискретного ряда определяется как варианта, имеющая наибольшую частоту.

Мода интервального ряда распределения: , где:

- нижняя граница модального интервала;

– величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным;

Медиана – величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части.

Для определения медианы (Me) прежде всего исчисляют ее порядковый номер по формуле и строят ряд накопленных частот. Накопленной частоте, которая равна порядковому номеру медианы или превышает его, в дискретном вариационном ряду соответствует варианта, являющаяся медианой, а в интервальном вариационном ряду – медианный интервал. Расчет медианы в интервальном вариационном ряду проводится по следующей формуле:

, где

- нижняя граница медианного интервала;

- величина медианного интервала;

- накопленная частота интервала, предшествующего медианному;

- частота медианного интервала;

Методика определения квартилей и децилей аналогична методике исчисления медианы.

Формула для расчета первого квартиля Q₁ в интервальном ряду распределения:

, где

- нижняя граница интервала, содержащего первый квартиль

- накопленная частота интервала, предшествующего интервалу, содержащему первый квартиль;

- частота интервала, содержащего первый квартиль.

Формула для расчета третьего квартиля Q₃ в интервальном ряду распределения имеет вид:

, где

- нижняя граница интервала, содержащего третий квартиль

- накопленная частота интервала, предшествующего интервалу, содержащему третий квартиль;

- частота интервала, содержащего третий квартиль.