
- •Билет № 1
- •1. Теоремы о взаимосвязи опорных решений задачи линейного программирования и угловых точек области допустимых решений.
- •Билет № 3
- •1. Необходимые и достаточные условия разрешимости транспортной задачи.
- •Билет № 4
- •1. Свойство системы ограничений транспортной задачи. Взаимосвязь линейной зависимости векторов-условий и циклов.
- •Билет № 5
- •1. Методы построения опорного решения транспортной задачи. Метод вычёркивания.
- •Билет № 6
- •Билет № 8
- •2. Теорема об единичном базисе.
- •Билет № 9
- •2. Теорема о двух линейно независимых системах векторов.
- •Билет № 10
- •2. Теорема о двух системах векторов, которым соответствуют равносильные системы уравнений.
- •Билет № 12
- •2. Общая теория систем уравнений. Теорема Кронекера-Капелли.
- •Билет № 13
- •2. Фундаментальная система решений однородной системы уравнений, теорема о её существовании.
- •Билет № 14
- •2. Необходимые и достаточные условия существования обратной матрицы.
- •Билет № 15
- •1. Построение начального опорного решения и переход от одного опорного решения к другому в симплексном методе (вывод формул).
- •Билет № 16
- •Теорема об улучшении опорного решения, её следствия.
- •Билет № 17
- •1. Теоремы о взаимосвязи опорных решений и угловых точек области допустимых решений.
- •Билет № 18
- •1. Метод искусственного базиса решения задач линейного программирования, его обоснование. Леммы и теорема об оптимальности опорного решения.
- •Билет № 20
- •Обоснование метод искусственного базиса решения задач линейного программирования. Теорема об отсутствии оптимального решения ввиду неограниченности целевой функции.
- •Билет № 21
- •1. Первая теорема двойственности, её доказательство.
- •Билет № 22
- •Вторая теорема двойственности, её доказательство.
- •Билет № 29
- •1. Теорема о виде области допустимых решений задачи линейного программирования.
- •Билет № 30
- •1. Теорема об улучшении опорного решения, её следствия.
Билет № 1
1. Теоремы о взаимосвязи опорных решений задачи линейного программирования и угловых точек области допустимых решений.
Теорема 3.4. Любое опорное решение является угловой точкой области допустимых решений.
Д о к а з а т е л ь с т в о (от противного).
Пусть
![]() опорное решение
с базисом
опорное решение
с базисом
![]() некоторой задачи с системой ограничений
некоторой задачи с системой ограничений
![]() .
Предположим, что X
не является угловой точкой, тогда оно
является выпуклой линейной комбинацией
каких-либо точек области допустимых
решений, например,
.
Предположим, что X
не является угловой точкой, тогда оно
является выпуклой линейной комбинацией
каких-либо точек области допустимых
решений, например,
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
.
Так как
последние n
m координат вектора
X равны нулю, а
![]() и
и
![]() положительные, то последние n
m координат
векторов
и
также равны нулю, т.е.
положительные, то последние n
m координат
векторов
и
также равны нулю, т.е.
![]() и
и
![]() .
.
Подставим
![]() в систему ограничений задачи:
в систему ограничений задачи:
![]()
![]() .
.
Вычтем из первого равенства второе. Получим
![]()
Так как векторы
![]() образуют базис, то они линейно независимые,
а потому данное равенство может
выполнятся только тогда, когда все
коэффициенты при векторах равны нулю,
т.е.
образуют базис, то они линейно независимые,
а потому данное равенство может
выполнятся только тогда, когда все
коэффициенты при векторах равны нулю,
т.е.
![]()
Отсюда получаем
![]() Следовательно,
Следовательно,![]() ,
и опорное решение X
не является выпуклой линейной
комбинацией каких-либо допустимых
решений, а является угловой точкой
области допустимых решений.
,
и опорное решение X
не является выпуклой линейной
комбинацией каких-либо допустимых
решений, а является угловой точкой
области допустимых решений.
Теорема 3.5. Любая угловая точка области допустимых решений является опорным решением.
Д о к а з а т е л ь с т в о. Пусть
![]() угловая точка области допустимых решений
и
угловая точка области допустимых решений
и
![]() при
j = 1, 2,…, m.
Чтобы доказать, что это решение является
опорным, достаточно показать, что
векторы
при
j = 1, 2,…, m.
Чтобы доказать, что это решение является
опорным, достаточно показать, что
векторы
![]() ,
соответствующие положительным
координатам решения, являются линейно
независимыми.
,
соответствующие положительным
координатам решения, являются линейно
независимыми.
Предположим, что эти векторы линейно
зависимы. Тогда существует ненулевой
набор чисел
![]() такой, что
такой, что
![]()
![]() (3.2)
(3.2)
Так как X допустимое решение, то имеет место равенство
![]() (3.3)
(3.3)
Умножим соотношение (3.2) на некоторое число и прибавим к равенству (3.3), получим
![]() ,
,
т.е. вектор
![]() является решением системы ограничений
задачи. Аналогично можно показать, что
решением системы является также вектор
является решением системы ограничений
задачи. Аналогично можно показать, что
решением системы является также вектор
![]() .
.
Для того, чтобы эти векторы
и
удовлетворяли условиям неотрицательности,
достаточно малое число
выберем так, что
![]() .
Это возможно, так как
при
j = 1, 2,…, m..
При таком выборе числа
векторы
и
являются
допустимыми. Нетрудно видеть, что
.
Это возможно, так как
при
j = 1, 2,…, m..
При таком выборе числа
векторы
и
являются
допустимыми. Нетрудно видеть, что
![]() ,
т.е. X является
выпуклой линейной комбинацией
и
.
Это противоречит тому, что X
является угловой точкой. Следовательно,
векторы
линейно независимые, и решение X
является опорным.
,
т.е. X является
выпуклой линейной комбинацией
и
.
Это противоречит тому, что X
является угловой точкой. Следовательно,
векторы
линейно независимые, и решение X
является опорным.
Билет № 3
1. Необходимые и достаточные условия разрешимости транспортной задачи.
Теорема 6.1. Для того, чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей
 ,
,
т. е. задача должна быть с правильным балансом.
До к а з а т е л ь с т в о. Необходимость. Пусть задача имеет допустимое решение
![]() ,
,
![]() ,
i = 1, 2, ..., m;
j = 1, 2, ..., n.
,
i = 1, 2, ..., m;
j = 1, 2, ..., n.
Докажем, что
.
Подставим
![]() в уравнения системы ограничений (6.2) и
(6.3), получим
в уравнения системы ограничений (6.2) и
(6.3), получим
 ,
i = 1, 2, ..., m,
,
i = 1, 2, ..., m,
 ,
j = 1, 2, ..., n
.
,
j = 1, 2, ..., n
.
Просуммируем первую и вторую группы тождеств по отдельности:
 и
и
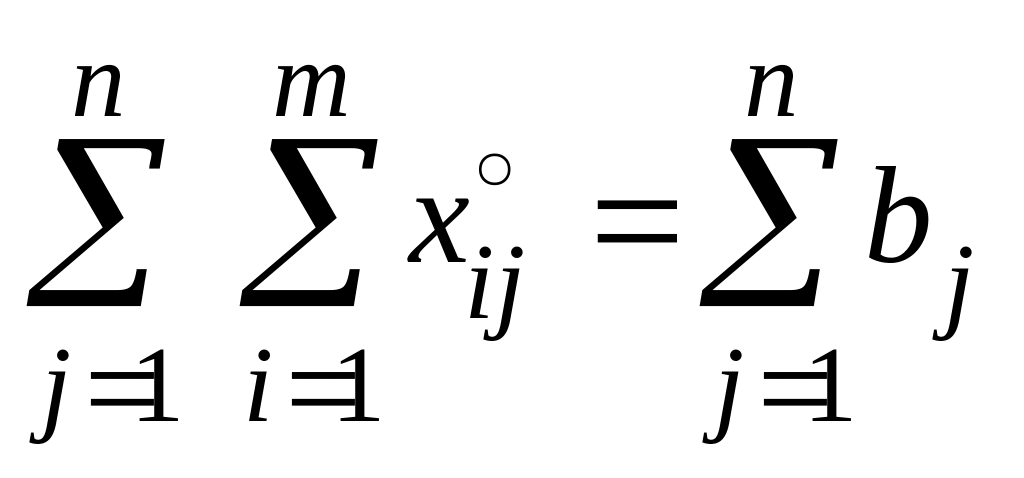 .
.
Отсюда следует, что задача имеет правильный баланс .
Достаточность. Пусть задача имеет правильный баланс
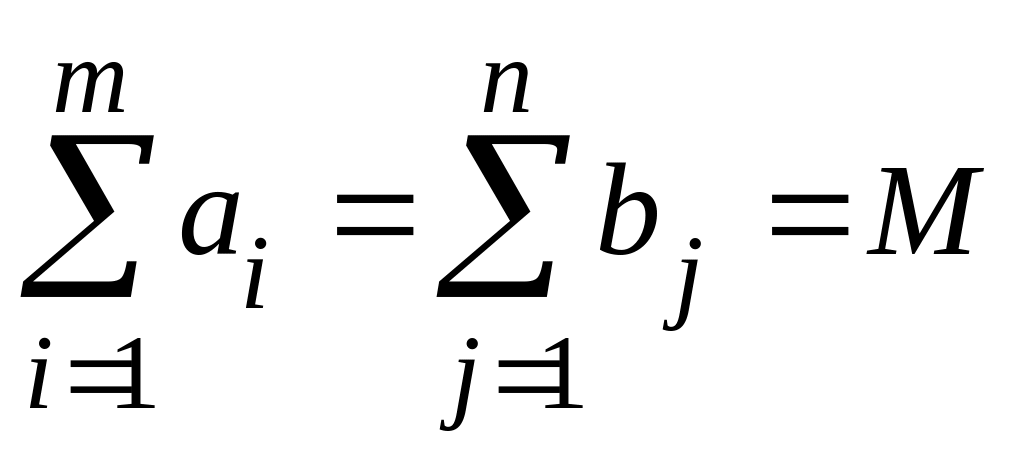 .
.
Докажем, что в этом случае задача имеет оптимальное решение.
Сначала убедимся в том, что область
допустимых решений задачи является
непустым множеством. Проверим, что
![]() ,
i = 1, 2, ..., m;
j = 1, 2, .., n
является допустимым решением. Подставим
в левые части уравнений системы
ограничений (6.2), (6.3), получим
,
i = 1, 2, ..., m;
j = 1, 2, .., n
является допустимым решением. Подставим
в левые части уравнений системы
ограничений (6.2), (6.3), получим
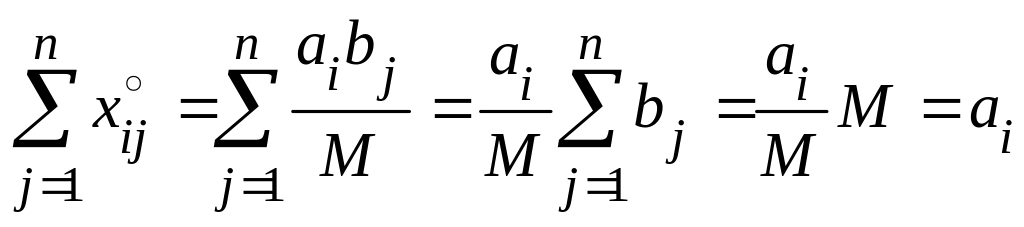 ,
i = 1, 2, ..., m,
,
i = 1, 2, ..., m,
 ,
j = 1, 2, ..., n,
,
j = 1, 2, ..., n,
т. е. уравнения обращаются в тождества.
Очевидно, что
![]() удовлетворяет и условиям неотрицательности.
удовлетворяет и условиям неотрицательности.
Далее покажем, что существует оптимальное
решение. Очевидно, стоимости перевозок
единиц груза ограничены сверху и снизу
![]() ,
где C и D
постоянные величины. Можно записать
,
где C и D
постоянные величины. Можно записать
 .
.
Следовательно, целевая функция ограничена на множестве допустимых решений и, как всякая непрерывная функция, достигает своего наименьшего и наибольшего значений.
