Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Национальный исследовательский ядерный университет «МИФИ»

Волгодонский инженерно-технический институт - филиал нияу мифи

Конспект лекций

по теме:

«Функции нескольких переменных»

Волгодонск

2010

Функции нескольких переменных.

1Функции 2 переменных, способы задания, область определения.

Определение: Если каждой точке P(x;y), принадлежащей плоской области D, ставится в соответствие единственное значение z, принадлежащее области E, то говорят, что задана функция двух переменных , действующая из D в E(DE).

Область D называется областью определения функции, область E-множество значений функции, x и y аргументы функции, z-значение функции.

Способы задания функции:

Табличный (с помощью таблицы).

x	0	-2
y	2	0
z	3	4

Аналитический (с помощью формулы).

Например: , , .

Областью определения функции двух переменных является множество пар (x,y), при которых выражение, задающее функцию, имеет смысл.

Пример: Найти область определения функции.

.

.

.

Графический.

Графиком функции называется множество точек пространства с координатами (x,y,f(x,y)),таких, что (x,y)D(z)-область определения функции. Для функции двух переменных графиком является некоторая поверхность.

2Предел и непрерывность функции 2 переменных.

Обозначим через  расстояние между точками M(x,y) и M(x₀,y₀),тогда . Рассмотрим неравенство < или . Это неравенство задает внутреннюю область круга с центром в точке M₀ и радиусом .

Определение: Число А называется пределом функции при xx₀, yy₀, если для любого, сколь угодно малого положительного , найдется , зависящее от , положительное, такое, что из неравенства , будет следовать неравенство . из неравенства  . =

Замечание: Все теоремы о пределах для функций с одной переменной справедливы и для функций многих переменных.

Определение: Функция называется непрерывной в точке M₀(x₀,y₀),если 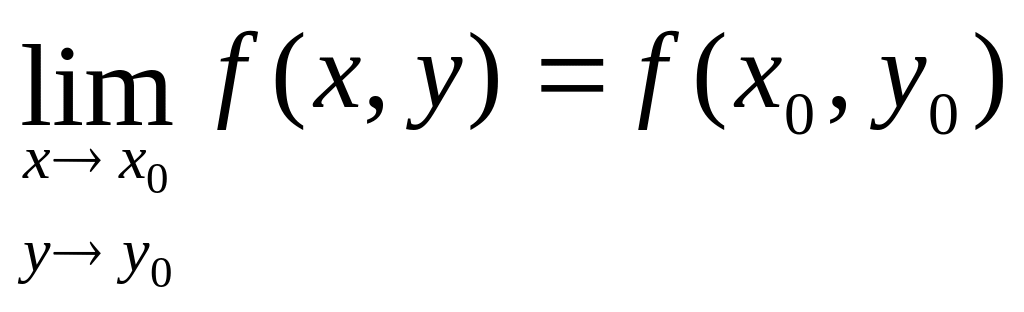,то есть если предел совпадает со значением функции.

3Частные производные функций 2 переменных и их геометрический смысл.

Пусть функция определена в окрестности точки M(x,y) и в самой точке М. Дадим переменной x приращение x (xx+x), а переменную y оставим без изменения (yy)так, чтобы точка M₁(x+x; y)указанной окрестности, тогда функция получит приращение _xz по переменной x: .

Если существует предел при x0 отношения приращения функции к приращению аргумента, то он называется частной производной функции z по переменной x и обозначается : .

Если существует предел при отношения приращения функции к приращению аргумента, то он называется частной производной функции z по переменной y и обозначается : .

При вычислении частных производных все переменные, кроме одной (по которой берется производная) считаются константами. Берем функцию двух переменных, частное по x, y – константа.

, y-const., x-const или y,z,t-const., x,y,t-const..

Вычислим частное производное функции двух переменных.

; (y-const); (x-const).

-функция от трех переменных U(x,y,z), (2x-0+1y) .

.

Частные дифференциалы функции двух переменных.

Так как функция при фиксированном y зависит только от x, то она фактически является функцией одной переменной и для нее можно ввести понятие дифференциала.

Определение: Частным дифференциалом функции по переменной x называется главная часть частного приращения функции по переменной x, линейная относительно x.

– частный дифференциал по переменной x,

Аналогично можно ввести понятие частного дифференциала функции по переменной y: .