5.3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов

Физическая величина, равная работе сторонних сил по перемещению положительного единичного заряда вдоль всей цепи, включая источник тока, называется электродвижущей силой источника тока (ЭДС) :

. (5.15)

Работа сторонних сил вдоль замкнутой цепи

, (5.16)

где E^* – напряженность поля сторонних сил.

Тогда

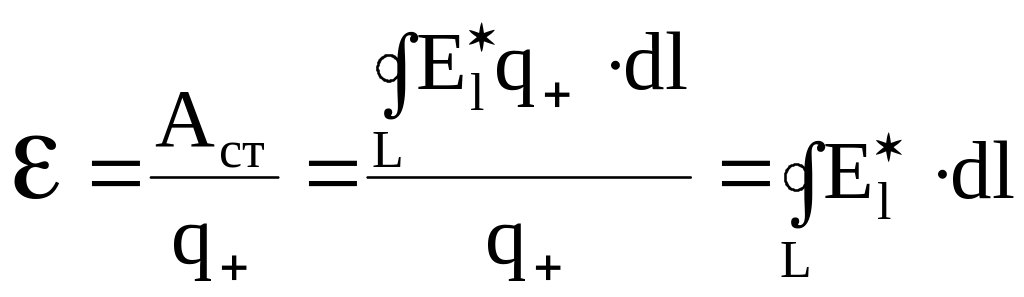. (5.17)

При движении зарядов в проводнике кроме сторонних сил на них действуют силы электростатического поля ( ). Следовательно, в любой точке цепи на заряд q действует результирующая сила:

. (5.18)

Работа, совершаемая этой силой на участке 1 – 2,

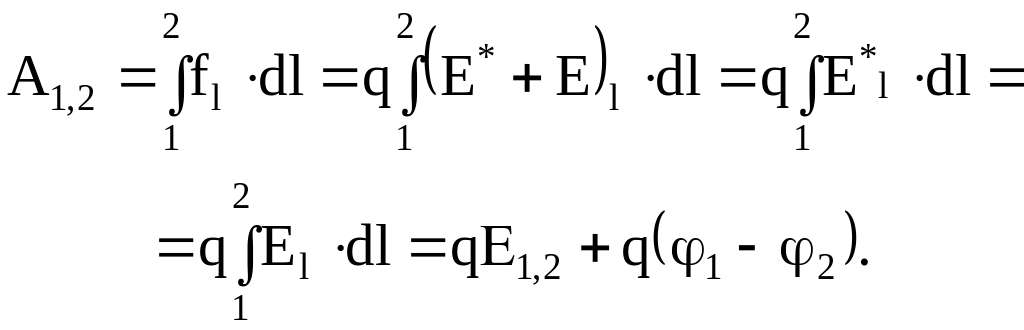(5.19)

Физическая величина, численно равная работе сторонних и электрических сил по перемещению положительного единичного заряда на данном участке цепи, называется падением напряжения или напряжением на данном участке цепи:

. (5.20)

Если на участке цепи отсутствует ЭДС ( ), то

. (5.21)

При ₁ - ₂ = 0,

. (5.22)

Измеряются , U, (₁ - ₂) в системе СИ в вольтах (1 В).

Лекция 6. Классическая электронная теория проводимости металлов. Законы постоянного тока

Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах. Электрическое сопротивление проводников. Изменение сопротивления проводников от температуры и давления. Сверхпроводимость. Соединения сопротивлений: последовательное, параллельное, смешанное. Шунтирование электроизмерительных приборов. Добавочные сопротивления к электроизмерительным приборам. Правила (законы) Кирхгофа и их применение к расчету простейших электрических цепей. Закон Джоуля-Ленца в дифференциальной и интегральной формах. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (КПД) источника постоянного тока.

6.1. Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах

Классическая электронная теория проводимости металлов объясняет различные электрические свойства веществ существованием и движением в них так называемых квазисвободных электронов проводимости. Электроны проводимости при этом рассматриваются как электронный газ, подобный идеальному газу молекулярной физики.

До открытия электронов было экспериментально показано, что прохождение тока в металлах не связано, в отличие от тока в жидких электролитах, с переносом вещества металла. Опыт состоял в том, что через контакт двух различных металлов, например золота и серебра, в течение времени, исчисляемого многими месяцами, пропускали электрический ток. После чего исследовался материал вблизи контактов. Было показано, что никакого переноса вещества через границу различных металлов не наблюдается и вещество по различные стороны границы раздела имеет тот же состав, что и до пропускания тока. Опыты доказали, что атомы и молекулы металлов не принимают участия в переносе электрического тока, но они не ответили на вопрос о природе носителей заряда в металлах.

Прямым доказательством, что электрический ток в металлах обусловливается движением электронов, были опыты Толмена и Стюарда, проведенные в 1916 г. Идея этих опытов была высказана Мандельштамом и Папалекси в 1913 г.

Представим себе проводящую катушку, которая может вращаться вокруг своей оси. Концы катушки с помощью скользящих контактов замкнуты на гальванометр. Если находящуюся в быстром вращении катушку резко затормозить, то свободные электроны в проволоке продолжают движение по инерции, в результате чего гальванометр должен зарегистрировать импульс тока.

Обозначим линейное ускорение катушки при торможении – a. Оно направлено по касательной к поверхности катушки. При достаточно плотной намотке и тонких проводах можно считать, что ускорение направлено вдоль проводов. При торможении катушки к каждому свободному электрону приложена сила инерции F_ин = m_ea, направленная противоположно ускорению. Под ее действием электрон ведет себя в металле так, как если бы на него действовало эффективное электрическое поле с напряженностью

. 6.1)

Поэтому эффективная электродвижущая сила в катушке, обусловленная инерцией свободных электронов,

, (6.2)

где L – длина провода на катушке.

Все точки провода тормозятся с одинаковым ускорением, и поэтому ускорение вынесено за знак интеграла.

С учетом формулы (6.2) запишем закон Ома для замкнутой цепи в виде

, (6.3)

где I – сила тока в замкнутой цепи;

R – сопротивление всей цепи, включая сопротивление проводов катушки, проводов внешней цепи и гальванометра.

Количество электричества, протекшее через поперечное сечение проводника в течение времени dt при силе тока I,

. (6.4)

Поэтому в течение времени торможения катушки от начальной линейной скорости v_o до полной остановки через гальванометр пройдет количество электричества

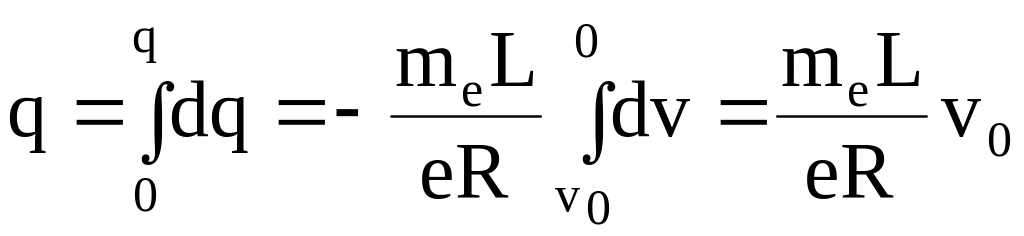. (6.5)

Значение q определяется по гальванометру, а значения L, R, v_o известны. Поэтому можно найти как знак, так и абсолютное значение e/m_e. Эксперименты показали, что e/m_e соответствует отношению заряда электрона к его массе. Таким образом, было доказано, что наблюдаемый с помощью гальванометра ток обусловлен движением электронов.

В отсутствие электрического поля в проводниках электроны проводимости движутся хаотично, в произвольных направлениях со скоростями, обусловленными температурой, т.е. с так называемой тепловой скоростью u.

Через определенный промежуток времени t = , двигаясь по прямой, электрон проводимости может провзаимодействовать с ионом кристаллической решетки или с другим электроном проводимости. В результате такого взаимодействия, а оно считается в классической теории проводимости абсолютно упругим, сохраняются полные импульс и энергия, а величина и направление скорости движения могут измениться. Предельным является случай, когда через время, равное  (время свободного пробега), направление скорости теплового движения электрона проводимости изменяется на противоположное. Время свободного пробега зависит от природы вещества и тем меньше, чем чаще происходят взаимодействия. Между соударениями (взаимодействиями) со скоростью u ничего не происходит.

П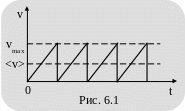 ри наложении электричес-кого поля с напряженностью E под действием силы F = eE электроны проводимости приоб-ретают некоторое ускорение a и направленное движение с изменяющейся скоростью от v_o =0 до v = v_max за время t = .

Изменение скорости направленного движения электрона проводимости происходит до его взаимодействия (рис. 6.1). В результате взаимодействия эта скорость так же может измениться как по величине, так и по направлению.

Если в единице объема проводника n электронов проводимости, которые в некоторый момент времени t обладают скоростью v, то можно определить заряд, прошедший через некоторую площадку S, расположенную перпендикулярно направлению скорости движения электронов проводимости:

, (6.6)

где <v> - средняя скорость упорядоченного движения электронов проводимости.

Сила (величина) тока в проводнике в этом случае

. (6.7)

Плотность тока проводимости

. (6.8)

В векторной форме

. (6.9)

Согласно (6.8) для определения плотности электрического тока в проводнике необходимо определить среднюю скорость упорядоченного движения электронов проводимости.

Средняя скорость упорядоченного движения в данном случае может быть определена по формуле

, (6.10)

т.к. в начальный момент времени t=0, когда отсутствует электрическое поле, v_o=0.

Максимальная скорость упорядоченного движения, которую приобретает электрон под действием электрического поля за время свободного пробега,

,

где a – ускорение, приобретаемое электроном проводимости под действием электрического поля;

 – время пробега электрона проводимости от взаимодействия до взаимодействия.

На основании второго закона Ньютона F = ma, где F - кулоновская сила,

F = eE.

Имеем:

;

;

. (6.11)

Для средней скорости упорядоченного движения электронов проводимости получим

. (6.12)

Зная среднюю скорость теплового движения электронов проводимости и среднее расстояние, проходимое ими от взаимодействия до взаимодействия, можно определить время между двумя последующими взаимодействиями:

. (6.13)

Сделав подстановку и необходимые преобразования, для плотности тока проводимости будем иметь

, (6.14)

где - удельная электропроводность металла проводника.

В векторной форме

. (6.15)

Выражения (6.14) и (22.15) являются математической формой записи закона Ома в дифференциальной форме.

Закон Ома в дифференциальной форме справедлив для любых проводников, любых токов, характеризует плотность тока проводимости в любой точке проводника.

Из закона Ома в дифференциальной форме можно получить закон Ома в интегральной форме для замкнутой (или полной) цепи. Для чего выражение (6.15) умножим на величину элементарного участка цепи dl:

,

где ; ; .

Таким образом, имеем

или

; . (6.16)

Проинтегрировав выражение (6.16) по замкнутому контуру L, получим

, (6.17)

где – сопротивление внешнего и внутреннего участков цепи;

– ЭДС, действующая в замкнутой цепи, численно равная циркуляции вектора напряженности поля сторонних сил;

– разность потенциалов между двумя рассматриваемыми точками замкнутой цепи.

Для замкнутой цепи

(₁ - ₂) = 0; .

Таким образом, имеем

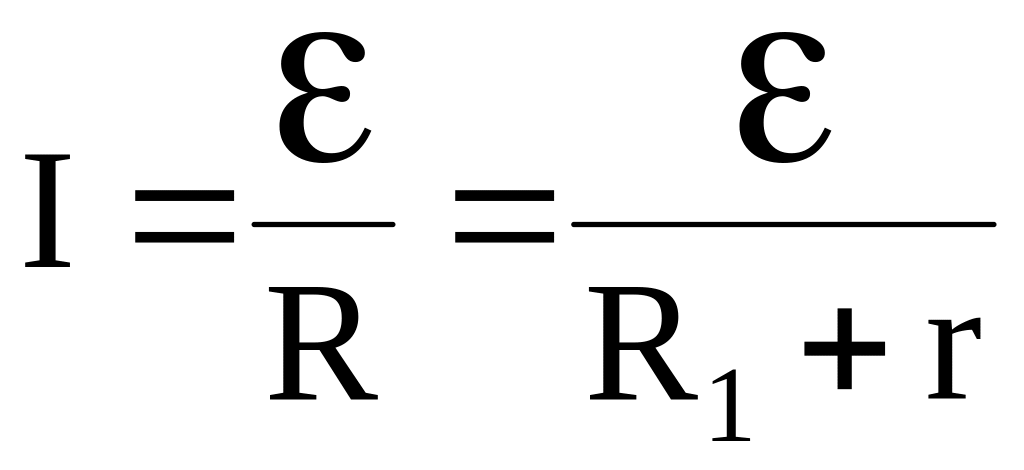или , (6.18)

где R₁ – сопротивление внешнего участка цепи;

r – внутреннее сопротивление источника тока.

Из формулы (6.18)

. (6.19)

Следовательно, ЭДС уравновешивает падение напряжения во внешней и внутренней цепи и тем самым обеспечивает непрерывное движение электронов проводимости.

Если цепь не замкнута и в ней отсутствует ЭДС, то

, а . (6.20)

Выражения (6.18) и (6.20) являются математической формой записи закона Ома, соответственно, для полной (замкнутой) цепи и участка цепи, который был открыт им экспериментально. Сила тока в цепи прямопропорциональна ЭДС (напряжению на участке цепи) и обратно пропорциональна сопротивлению цепи.